こんにちは、リンス(@Lins016)です。
今回は空間ベクトルと平面の方程式について学習していこう。
平面の方程式
空間中の平面の方程式は\(\small{ \ ax+by+cz+d=0 \ }\)の形で表すことができる。今回はこの平面の方程式を複数の方法で導いてみよう。
・一般形\(\small{ \ ax+by+cz+d=0 \ }\)
平面の法線ベクトル\(\small{ \ \overrightarrow{n}=(a, \ b, \ c) \ }\)
平面上の点\(\small{ \ \mathrm{A}(x_0, \ y_0, z_0) \ }\)を通る平面の方程式
\(\small{ \ a(x-x_0)+b(y-y_0)+c(z-z_0)=0 \ }\)
平面の方程式
まず空間中の平面は\(\small{ \ 3 \ }\)点を通ることで決まることを覚えておこう。\(\small{ \ 2 \ }\)点だと直線だけど、\(\small{ \ 3 \ }\)点だと平面になるからね。
\(\small{ \ 3 \ }\)点を通る平面の方程式は\(\small{ \ ax+by+cz+d=0 \ }\)に\(\small{ \ 3 \ }\)点の座標を代入して、連立方程式を解いて\(\small{ \ a:b:c:d \ }\)の比を求めよう。

この連立方程式を解いても解は\(\small{ \ a:b:c:d \ }\)の比がでるだけだから、最初から\(\small{ \ a=1 \ }\)として\(\small{ \ x+by+cz+d=0 \ }\)で求めてもいいんだけど、\(\small{ \ a=0 \ }\)だったら困るよね。
この考え方は図形と方程式で学習した直線の方程式の求め方と同じだからね。
この考え方が「?」な人は一度復習しておこう。
直線の方程式では傾き\(\small{ \ m \ }\)で\(\small{ \ (a, \ b) \ }\)を通るとき、\(\small{ \ y=m(x-a)+b \ }\)ってできたけど、平面も同じように少し工夫して考えることができるんだ。
平面が\(\small{ \ (x_0, \ y_0, \ z_0) \ }\)を通るとき、平面の方程式は\(\small{ \ a(x-x_0)+b(y-y_0)+c(z-z_0)=0 \ }\)になる。
確かに左辺の\(\small{ \ (x, \ y, \ z) \ }\)に\(\small{ \ (x_0, \ y_0, \ z_0) \ }\)を代入すると\(\small{ \ 0 \ }\)になるし、展開すると平面の方程式の形になってるから、この\(\small{ \ a(x-x_0)+b(y-y_0)+c(z-z_0)=0 \ }\)は\(\small{ \ (x_0, \ y_0, \ z_0) \ }\)を通る平面の方程式って言えるよね。
だから\(\small{ \ 3 \ }\)点だと平面の方程式を求める場合、まずは\(\small{ \ 1 \ }\)点を利用して\(\small{ \ a(x-x_0)+b(y-y_0)+c(z-z_0)=0 \ }\)の形で平面の方程式をおいて、残りの\(\small{ \ 2 \ }\)点を代入して平面の方程式を求めよう。

\(\small{ \ x, \ y, \ z \ }\)の係数の\(\small{ \ a, \ b, \ c \ }\)のどれかが\(\small{ \ 0 \ }\)だったら、軸に平行な平面になるから注意しよう。
\(\small{ \ \mathrm{A}(1, \ 2, \ 2) \ }\)、\(\small{ \ \mathrm{B}(4, \ -2, \ 8) \ }\)、\(\small{ \ \mathrm{C}(-2, \ 3, \ 5) \ }\)を通る平面の方程式を求めよ。
\(\small{ \ \mathrm{A}(1, \ 2, \ 2) \ }\)を通る平面の方程式は
これは\(\small{ \ \mathrm{B}(4, \ -2, \ 8) \ }\)、\(\small{ \ \mathrm{C}(-2, \ 3, \ 5) \ }\)を通るから代入すると
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
3a-4b+6c=0\cdots②\\
-3a+b+3c=0\cdots③
\end{array}
\right.
\end{eqnarray}
\ }\)
\(\small{ \ ②+③ \ }\)より\(\small{ \ -3b+9c=0 \ }\)\(\small{ \ \therefore b=3c\cdots④ \ }\)
\(\small{ \ ④ \ }\)を\(\small{ \ ② \ }\)に代入して
\(\small{ \ 3a-4(3c)+6c=0 \ }\)
\(\small{ \ 3a-6c=0 \ }\)\(\small{ \ \therefore a=2c\cdots⑤ \ }\)
\(\small{ \ ④, \ ⑤ \ }\)を\(\small{ \ ① \ }\)に代入
\(\small{ \ 2c(x-1)+3c(y-2)+c(z-2)=0 \ }\)
\(\small{ \ \therefore 2x+3y+z-10=0 \ }\)

っておくことでだいぶ計算が楽になるから、常にこの方法で求めるようにしよう。
平面に垂直なベクトル
\(\small{ \ ax+by+cz+d=0 \ }\)の平面に垂直なベクトルを、この平面の法線ベクトルっていうんだ。
法線ベクトルは、この平面に垂直なベクトルだから、大きさが\(\small{ \ 1 \ }\)のベクトルや大きさが\(\small{ \ 3 \ }\)のベクトルとか無数にある。
ただ\(\small{ \ ax+by+cz+d=0 \ }\)の法線ベクトルは、この方程式の\(\small{ \ x, \ y, \ z \ }\)の係数をとった\(\small{ \ (a, \ b, \ c) \ }\)もその\(\small{ \ 1 \ }\)つってことが知られているんだ。
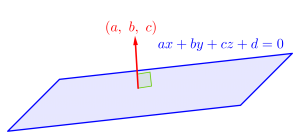
これかなり重要だから覚えててね。
このベクトル\(\small{ \ (a, \ b, \ c) \ }\)を実数倍すれば大きさは変えられるもんね。
平面の法線ベクトルは、平面上の\(\small{ \ 3 \ }\)点のうち\(\small{ \ 2 \ }\)点を結ぶベクトルを\(\small{ \ 2 \ }\)つ作って、これに垂直なベクトルが法線ベクトルになるから、内積を利用して求めよう。
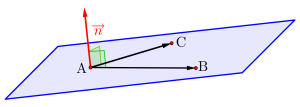
\(\small{ \ \mathrm{A}(1, \ 2, \ 2) \ }\)、\(\small{ \ \mathrm{B}(4, \ -2, \ 8) \ }\)、\(\small{ \ \mathrm{C}(-2, \ 3, \ 5) \ }\)のとき、\(\small{ \ \overrightarrow{\mathrm{AB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\)に垂直なベクトルのうち、最も簡単な整数のベクトルを求めよ。
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AB}}&=&\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\\
&=&4, \ -2, \ 8)-(1, \ 2, \ 2)\\
&=&(3, \ -4, \ 6) \ \end{eqnarray} }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AC}}&=&\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}}\\
&=&(-2, \ 3, \ 5)-(1, \ 2, \ 2)\\
&=&(-3, \ 1, \ 3) \ \end{eqnarray}}\)
\(\small{ \ \overrightarrow{\mathrm{AB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\)に垂直なベクトルを\(\small{ \ \overrightarrow{n}=(a, \ b, \ c) \ }\)とすると
\(\small{ \ \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{n}=0 \ }\)
\(\small{ \ (3, \ -4, \ 6)\cdot(a, \ b, \ c)=0 \ }\)
\(\small{ \ 3a-4b+6c=0\cdots① \ }\)
\(\small{ \ \overrightarrow{\mathrm{AC}}\cdot\overrightarrow{n}=0 \ }\)
\(\small{ \ (-3, \ 1, \ 3)\cdot(a, \ b, \ c)=0 \ }\)
\(\small{ \ -3a+b+3c=0\cdots② \ }\)
\(\small{ \ ①+② \ }\)より
\(\small{ \ -3b+9c=0 \ }\)より\(\small{ \ b=3c \ }\)
よって\(\small{ \ a=2c \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{n}&=&(a, \ b, \ c)\\
&=&(2c, \ 3c, \ c) \ \end{eqnarray}}\)
一番簡単な整数比のベクトルは\(\small{ \ (2, \ 3, \ 1) \ }\)

法線ベクトルを利用した平面の方程式
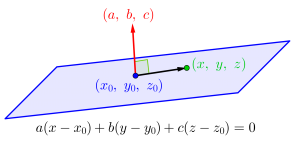
ここまでの流れでなんとなくわかったかもしれないけど、法線ベクトルと平面上にある\(\small{ \ 1 \ }\)点の座標がわかっていると簡単に平面を求めることができるよね。
だって法線ベクトル\(\small{ \ \overrightarrow{n}=(a, \ b, \ c) \ }\)と平面上の点\(\small{ \ (x_0, \ y_0, \ z_0) \ }\)から、平面の方程式は\(\small{ \ a(x-x_0)+b(y-y_0)+c(z-z_0)=0 \ }\)ってなるよね。
実はこれベクトル方程式から出来ていて、平面上の点のベクトル\(\small{ \ \overrightarrow{\mathrm{OA}}=(x_0, \ y_0, \ z_0) \ }\)と\(\small{ \ \overrightarrow{\mathrm{OP}}=(x, \ y, \ z) \ }\)とすると、\(\small{ \ \overrightarrow{\mathrm{AP}}=(x-x_0, \ y-y_0, \ z-z_0) \ }\)が法線ベクトルに垂直になるから
\(\small{ \ \overrightarrow{\mathrm{AP}}\cdot\overrightarrow{n}=0 \ }\)
\(\small{ \ \left(\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OP}}\right)\cdot\overrightarrow{n}=0 \ }\)
\(\small{ \ (x-x_0, \ y-y_0, \ z-z_0)\cdot(a, \ b, \ c)=0 \ }\)
\(\small{ \ \therefore a(x-x_0)+b(y-y_0)+c(z-z_0)=0 \ }\)
s+t+u=1を利用
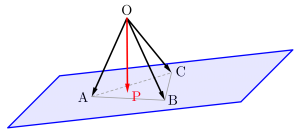
空間ベクトルって言えば基本は\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)の形だったよね。次はこの形から平面の方程式を考えてみよう。
\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C} \ }\)を通る平面上に\(\small{ \ \mathrm{P} \ }\)があるとき、\(\small{ \ s+t+u=1 \ }\)だったよね。
つまり
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}}\\
&=&(1-t-u)\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ \end{eqnarray}}\)
の形にすれば、\(\small{ \ \mathrm{P} \ }\)は平面\(\small{ \ \mathrm{ABC} \ }\)上にあることになるんだ。
成分表示の問題で\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)の形のまま考えることはあまりないけど、今回はこれで上の例題と同じ問題を考えてみよう。
\(\small{ \ \mathrm{A}(1, \ 2, \ 2) \ }\)、\(\small{ \ \mathrm{B}(4, \ -2, \ 8) \ }\)、\(\small{ \ \mathrm{C}(-2, \ 3, \ 5) \ }\)のとき、\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)から平面の方程式を求めよ。
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)
&=&(s+4t-2u, \ 2s-2t+3u, \ 2s+8t+5u) \ \end{eqnarray}}\)
\(\small{ \ \mathrm{P} \ }\)は平面\(\small{ \ \mathrm{ABC} \ }\)上にあるから
\(\small{ \ s+t+u=1 \ }\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=1+3t-3u\cdots① \\
y=2-4t+u\cdots② \\
z=2+6t+3u\cdots③
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ ①+②\times3 \ }\)より
\(\small{ \ t=-\displaystyle\frac{x+3y-7}{9}\cdots④ \ }\)
\(\small{ \ ④ \ }\)を\(\small{ \ ② \ }\)に代入して
\(\small{ \ u=-\displaystyle\frac{4}{9}x-\displaystyle\frac{1}{3}y+\displaystyle\frac{10}{9}\cdots⑤ \ }\)
\(\small{ \ ④, \ ⑤ \ }\)を\(\small{ \ ③ \ }\)に代入して
これを整理して
\(\small{ \ 2x+3y+z-10=0 \ }\)

Point 空間ベクトルと平面の方程式
①\(\small{ \ 3 \ }\)点を通る平面の方程式の計算方法をマスターする
②平面の方程式と法線ベクトルの関係を覚える
\(\small{ \ \def\cenBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ }}\def\cenbox#1{\bbox[4px, border:1px solid gray]{\ #1\ }} \ }\)空間座標において\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A}(1, \ 0, \ 0) \ }\)、\(\small{ \ \mathrm{B}(0, \ 2, \ 0) \ }\)、\(\small{ \ \mathrm{C}(0, \ 0, \ 3) \ }\)を通る平面を\(\small{ \ \alpha \ }\)とする。\(\small{ \ \alpha \ }\)に関して原点\(\small{ \ \mathrm{O} \ }\)と対称な点\(\small{ \ \mathrm{D} \ }\)の座標は\(\small{ \ \cenbox{①} \ }\)であり、三角形\(\small{ \ \mathrm{OCD} \ }\)の面積は\(\small{ \ \cenbox{②} \ }\)である。
平面\(\small{ \ \alpha \ }\)の方程式は
\(\small{ \ \displaystyle \frac{x}{1}+\displaystyle \frac{y}{2}+\displaystyle \frac{z}{3}=1 \ }\)
\(\small{ \ \therefore 6x+3y+2z-6=0 \ }\)
原点\(\small{ \ \mathrm{O} \ }\)から平面\(\small{ \ \alpha \ }\)に下ろした垂線の足を\(\small{ \ \mathrm{H} \ }\)とすると
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OD}}&=&-2\overrightarrow{\mathrm{HO}}\\
&=&-2\cdot\displaystyle \frac{-6}{6^2+3^2+2^2}(6, \ 3, \ 2)\\
&=&\displaystyle \frac{12}{49}(6, \ 3, \ 2) \ \end{eqnarray}}\)
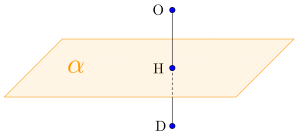
\(\small{ \ \therefore \ \mathrm{D}\left(\displaystyle \frac{72}{49}, \ \displaystyle \frac{36}{49}, \ \displaystyle \frac{24}{49}\right) \ }\)
\(\small{ \ \vert\overrightarrow{\mathrm{OC}}\vert=3 \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OD}}\vert=\displaystyle \frac{12}{7} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OC}}\cdot\overrightarrow{\mathrm{OD}}=\displaystyle \frac{72}{49} \ }\)
&=&\displaystyle \frac{1}{2}\sqrt{3^2\times\left(\displaystyle \frac{12}{7}\right)^2-\left(\displaystyle \frac{72}{49}\right)^2}\\
&=&\displaystyle \frac{1}{2\cdot7^2}\sqrt{36^2(7^2-2^2)}\\
&=&\displaystyle \frac{36}{2\cdot7^2}\sqrt{45}\\
&=&\displaystyle \frac{54}{49}\sqrt{5} \ \end{eqnarray}}\)

これは平面の\(\small{ \ x \ }\)軸の点\(\small{ \ (a, \ 0) \ }\)、\(\small{ \ y \ }\)軸上の点\(\small{ \ (0, \ b) \ }\)を通る直線の方程式が\(\small{ \ \displaystyle \frac{x}{a}+\displaystyle \frac{y}{b}=1 \ }\)と表すことができるのと同じ考え方だからね。

