こんにちは、リンス(@Lins016)です。
今回は空間ベクトルと2つの平面について学習していこう。
二つの平面の交線・角度
空間中の平面の方程式は前回学習したけど、今回はさらにもう一歩踏み込んで、平面と平面の交線やなす角などを空間ベクトルを利用して考えていこう。
・\(\small{ \ 2 \ }\)つの平面の交線
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
a_1x+b_1y+c_1z+d_1=0 \\
a_2x+b_2y+c_2z+d_2=0
\end{array}
\right.
\end{eqnarray} \ }\)
平面の方程式を連立して求める
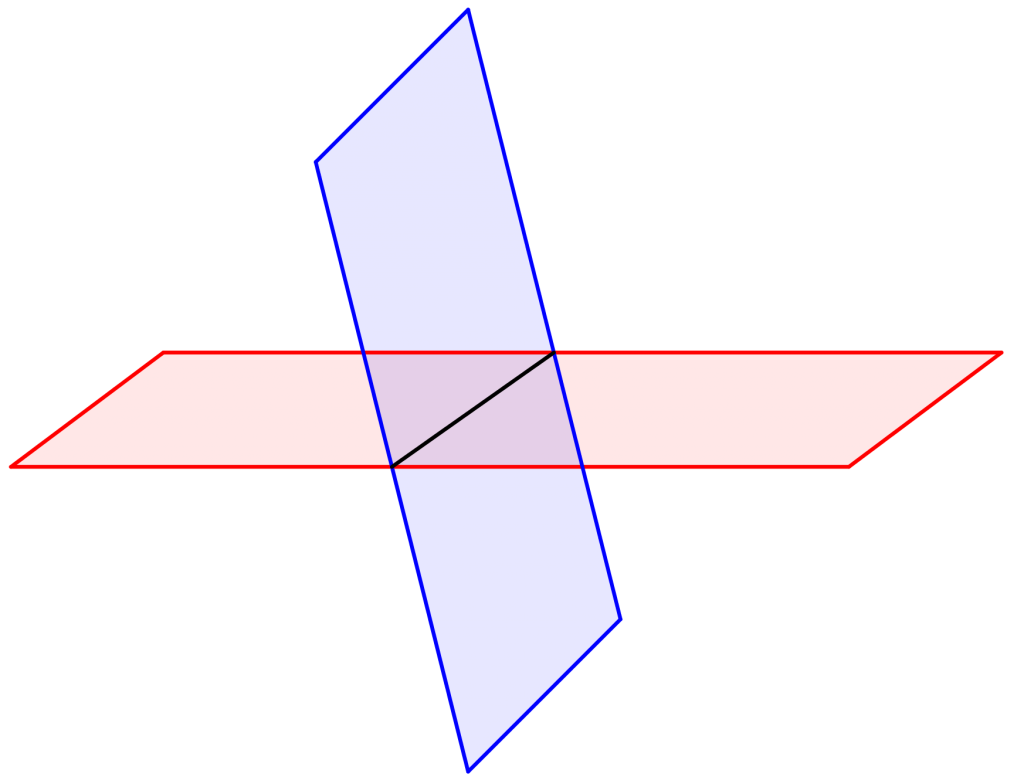
・\(\small{ \ 2 \ }\)つの平面のなす角
各平面の法線ベクトルのなす角と同じ

平面と平面の交線の求め方
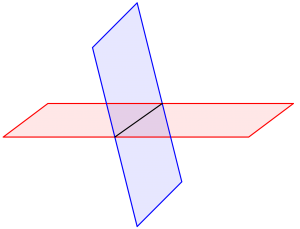
平面と平面が交わる部分は図のように線になるよね。まずこのことをしっかり確認しておこう。
\(\small{ \ 2 \ }\)つの平面の方程式から直線の方程式を求めていこう。
つまり\(\small{ \ 2 \ }\)つの平面の方程式を連立して直線の方程式を求めるってことね。
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
a_1x+b_1y+c_1z+d_1=0 \\
a_2x+b_2y+c_2z+d_2=0
\end{array}
\right.
\end{eqnarray} \ }\)
でもこの連立方程式って当然未知数\(\small{ \ x, \ y, \ z \ }\)の\(\small{ \ 3 \ }\)つに対して式は\(\small{ \ 2 \ }\)つだから、答えは\(\small{ \ 1 \ }\)つの文字を使った形になるからね。
この\(\small{ \ 1 \ }\)つの文字が媒介変数になるから、これを変形して直線の方程式の形に変形していこう。
平面\(\small{ \ \alpha:x+4y+z-5=0 \ }\)と平面\(\small{ \ \beta:2x+2y-z+2=0 \ }\)の交線の方程式を求めよ。
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x+4y+z-5=0\cdots① \\
2x+2y-z+2=0\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ ①+② \ }\)より
\(\small{ \ 3x+6y-3=0 \ }\)
\(\small{ \ \therefore x=-2y+1 \ }\)
これを\(\small{ \ ① \ }\)に代入すると
\(\small{ \ z=-2y+4 \ }\)
\(\small{ \ (x, \ y, \ z)=(-2y+1, \ y, \ -2y+4) \ }\)
\(\small{ \ y=t \ }\)とすると
\(\small{ \ (x, \ y, \ z)=(-2t+1, \ t, \ -2t+4) \ }\)
これを変形して
\(\small{ \ t=\displaystyle\frac{x-1}{-2}=y=\displaystyle\frac{z-4}{-2} \ }\)
\(\small{ \ \displaystyle\frac{x-1}{-2}=y=\displaystyle\frac{z-4}{-2} \ }\)

平面と平面のなす角
次は平面と平面のなす角を求めてみよう。って言っても\(\small{ \ 2 \ }\)つの平面のなす角を求めるのは難しいから、\(\small{ \ 2 \ }\)つの平面のなす角は、平面の法線ベクトルを求めて、法線ベクトルのなす角を求めよう。

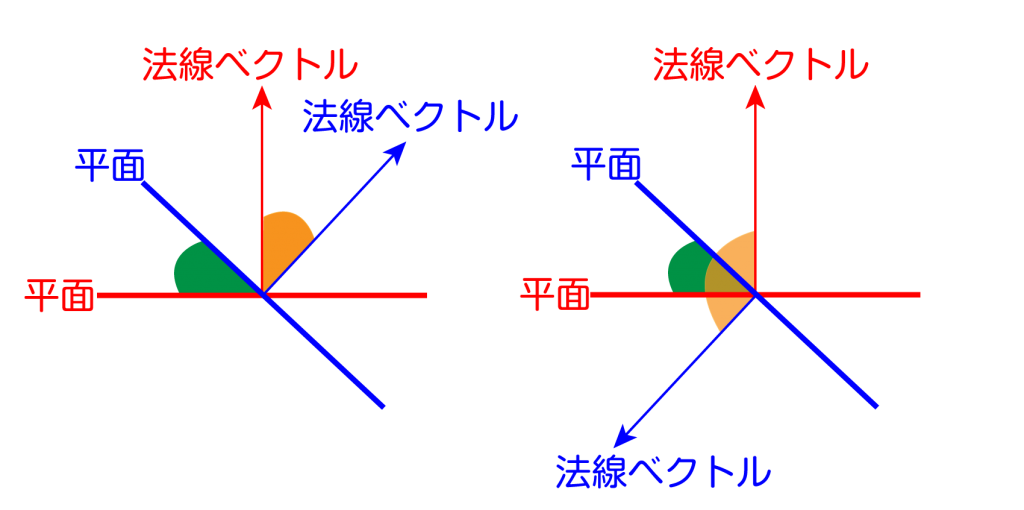
ただ法線ベクトルが下図のように思っていた向きと逆になっている場合、法線ベクトルのなす角が鈍角になる場合もあるから注意しよう。
鈍角になった場合その角を\(\small{ \ 180^{\circ} \ }\)から引けば、平面と平面のなす角の鋭角が求まるからね。それは図を見ても明らかだよね。
\(\small{ \ 2 \ }\)平面\(\small{ \ x+4y+z-5=0 \ }\)と\(\small{ \ 2x+2y-z+2=0 \ }\)のなす角を求めよ。
\(\small{ \ 2 \ }\)平面のなす角は、それぞれの法線ベクトルのなす角と同じである
平面\(\small{ \ x+4y+z-4=0 \ }\)の法線ベクトルは\(\small{ \ (1, \ 4, \ 1) \ }\)
平面\(\small{ \ 2x+2y-z+2=0 \ }\)の法線ベクトルは\(\small{ \ (2, \ 2, \ -1) \ }\)
&=&\displaystyle\frac{9}{9\sqrt{2}}=\displaystyle\frac{1}{\sqrt{2}} \ \end{eqnarray}}\)
\(\small{ \ \therefore \theta=45^{\circ} \ }\)
平面の法線ベクトルと交線の関係
図のように\(\small{ \ 2 \ }\)つの平面の交線は、それぞれの平面の法線ベクトルに垂直になる。
だから交線の方向ベクトルは法線ベクトルに垂直なベクトルを求めればすぐにわかるよね。
平面の方程式が\(\small{ \ a_1x+a_2y+a_3z+a_4=0 \ }\)と\(\small{ \ b_1x+b_2y+b_3z+b_4=0 \ }\)のとき、法線ベクトルは\(\small{ \ (a_1, \ a_2, \ a_3) \ }\)と\(\small{ \ (b_1, \ b_2, \ b_3) \ }\)になる。

この\(\small{ \ 2 \ }\)つのベクトルに垂直なベクトルは外積を利用すると
\(\small{ \ (a_2b_3-a_3b_2, \ a_3b1-a_1b_3, \ a_1b_2-a_2b_1) \ }\)になる。
つまりこのベクトルが交線の方向ベクトルになるんだ。
ただこの方向ベクトルから交線の方程式を求めるのは、結局最初にやった平面と平面を連立して求める方法と変わらないから、交線の方程式を求めるなら最初から平面の方程式を連立しよう。
あくまでこのやり方は交線の方向ベクトルが簡単に求められるってことで検算として使えるってことになるからね。
時間がある人はこの方向ベクトルに交線上の点を\(\small{ \ (p, \ q, \ r) \ }\)とおいてそれぞれの平面の方程式に代入して、\(\small{ \ p, \ q, \ r \ }\)を求めてみたらいいよ。そしたら最初の連立方程式と同じ式が出てくるから、方向ベクトル求めたのは無駄だったなってわかるからね。
2つの平面の交線とある点を通る平面の求め方
\(\small{ \ 2 \ }\)つの平面の交線とある点を通る平面について考えてみよう。
\(\small{ \ 2 \ }\)つの平面の方程式をそれぞれ、
\(\small{ \ ax+by+cz+d=0 \ }\)
\(\small{ \ px+qy+rz+s=0 \ }\)
とすると、この\(\small{ \ 2 \ }\)つの平面の交線を通る平面の方程式は、片方の方程式を\(\small{ \ k \ }\)倍して足そう。
\(\small{ \ ax+by+cz+d+k(px+qy+rz+s)=0 \ }\)
この式は展開すると
\(\small{ \ (a+kp)x+(b+kq)y+(c+kr)z+d+ks=0 \ }\)の形になるから平面の方程式だよね。
さらに交線は\(\small{ \ ax+by+cz+d=0 \ }\)と\(\small{ \ px+qy+rz+s=0 \ }\)を満たすから、当然\(\small{ \ k \ }\)倍して加えた\(\small{ \ ax+by+cz+d+k(px+qy+rz+s)=0 \ }\)も満たすよね。
つまりこの\(\small{ \ k \ }\)倍して加えた式は\(\small{ \ 2 \ }\)つの交線を通る平面の方程式ってことが言えるんだ。
この交線を通る平面は無数にあるから、問題文からある点を通るって与えられることで、平面の方程式が定まるんだ。

\(\small{ \ 2 \ }\)平面\(\small{ \ x+4y+z-5=0 \ }\)と\(\small{ \ 2x+2y-z+2=0 \ }\)の交線と\(\small{ \ \mathrm{A}(1, \ 1, \ 1) \ }\)を通る平面の方程式を求めよ。
\(\small{ \ x+4y+z-5=0 \ }\)と\(\small{ \ 2x+2y-z+2=0 \ }\)の交線を通る平面の方程式は
\(\small{ \ x+4y+z-5+k(2x+2y-z+2)=0 \ }\)
この平面は\(\small{ \ \mathrm{A}(1, \ 1, \ 1) \ }\)を通るから代入して
\(\small{ \ 1+5k=0 \ }\)
\(\small{ \ k=-\displaystyle\frac{1}{5} \ }\)
\(\small{ \ x+4y+z-5-\displaystyle\frac{1}{5}(2x+2y-z+2)=0 \ }\)
\(\small{ \ 5(x+4y+z-5)-(2x+2y-z+2)=0 \ }\)
\(\small{ \ \therefore x+6y+2z-9=0 \ }\)

Point 空間ベクトルと2つの平面
①交線は平面の方程式を連立して求める
②交線を通る平面は1つの方程式を\(\small{ \ k \ }\)倍して加える

