こんにちは、リンス(@Lins016)です。
今回は直線と平面の交点の求め方について学習していこう。
直線と平面の交点
空間中の直線と平面の交点の問題は、定められた直線が平面と交わる問題と、ある点から平面に下ろした垂線の問題がある。
どちらの問題も直線の方程式や平面の方程式をきちんと理解していないと自力で解けるようにはならないからね。
記事の途中で以前の記事のリンクを入れておくから、理解が不十分な人は復習しながら進めていこう。
\(\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}=\displaystyle\frac{z-z_0}{n} \ }\)と\(\small{ \ ax+by+cz+d=0 \ }\)の交点の求め方
①直線の方程式を\(\small{ \ (x, \ y, \ z)=(x_0+tl, \ y_0+tm, \ z_0+tn) \ }\)に変形
②\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=x_0+tl\\
y=y_0+tm\\
z=z_0+tn
\end{array}
\right.
\end{eqnarray} \ }\)を\(\small{ \ ax+by+cz+d=0 \ }\)に代入して\(\small{ \ t \ }\)を求める
③求めた\(\small{ \ t \ }\)を\(\small{ \ (x, \ y, \ z)=(x_0+tl, \ y_0+tm, \ z_0+tn) \ }\)に代入
直線と平面の交点(基本)
直線の方程式と平面の方程式が分かっている場合について考えていこう。
直線の方程式\(\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}=\displaystyle\frac{z-z_0}{n} \ }\)、平面の方程式\(\small{ \ ax+by+cz+d=0 \ }\)のとき、まずは直線の方程式を媒介変数を利用した形に変形しよう。
つまり\(\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}=\displaystyle\frac{z-z_0}{n} \ }\)という空間の直線の方程式を
\(\small{ \ \displaystyle\frac{x-x_0}{l}=\displaystyle\frac{y-y_0}{m}=\displaystyle\frac{z-z_0}{n}=t \ }\)とおいて、\(\small{ \ (x, \ y, \ z)=(x_0+tl, \ y_0+tm, \ z_0+tn) \ }\)としよう。
平面の方程式が\(\small{ \ ax+by+cz+d=0 \ }\)だから、この媒介変数\(\small{ \ t \ }\)を利用した直線上の座標を平面の方程式に代入して\(\small{ \ t \ }\)を求めればいいんだ。
その求めた\(\small{ \ t \ }\)の値を\(\small{ \ (x, \ y, \ z)=(x_0+tl, \ y_0+tm, \ z_0+tn) \ }\)に代入すれば交点の座標が求まるよね。
平面\(\small{ \ x+4y+z-5=0 \ }\)と直線\(\small{ \ \displaystyle\frac{x-2}{3}=\displaystyle\frac{y-1}{-2}=\displaystyle\frac{z+3}{3} \ }\)の交点の座標を求めよ。
\(\small{ \ \displaystyle\frac{x-2}{3}=\displaystyle\frac{y-1}{-2}=\displaystyle\frac{z+3}{3}=t \ }\)とおくと
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=3t+2 \\
y=-2t+1\\
z=3t-3
\end{array}
\right.
\end{eqnarray} \ }\)
これを平面の方程式\(\small{ \ x+4y+z-5=0 \ }\)に代入して
\(\small{ \ 3t+2+4(-2t+1)+(3t-3)-5=0 \ }\)
\(\small{ \ -2t-2=0 \ }\)
\(\small{ \ \therefore \ t=-1 \ }\)
よって求める交点の座標は
\(\small{ \ (x, \ y, \ z)=(-1, \ 3, \ -6) \ }\)

でも媒介変数\(\small{ \ t \ }\)を使わずに解こうとすると大変だから注意しよう。
垂線の方程式と垂線の足
次はある点から平面に下ろした垂線の足について考えてみよう。
そもそも「垂線の足って何?」って人いるかな?これは問題文でも出てくる言葉だから大丈夫だよね?
一応説明しておくと、「直線の垂線がその直線と交わる点」、または「平面の垂線がその平面と交わる点」のこと。
言葉じゃ分かりにくいから図を示すとこんな感じ。
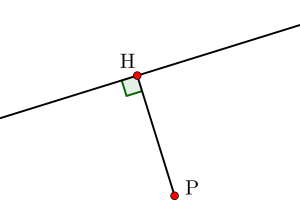

つまり垂線の足を求めるとき、ベクトルだと「垂直を利用して求めたい」ってことがなんとなくわかるよね。
垂直っていうと内積か法線ベクトルだよね。直線の場合は内積で、平面の場合は法線ベクトルになるかな。
平面\(\small{ \ ax+by+cz+d=0 \ }\)に垂直なベクトル(法線ベクトル)は\(\small{ \ (a, \ b, \ c) \ }\)だったよね。
つまりこの平面に垂直なベクトルが垂線を表す直線の方向ベクトルってことになるからね。
このことを頭に入れて次の例題を解いてみよう。
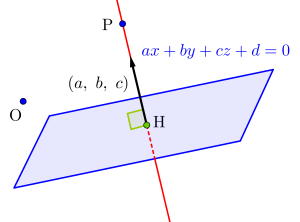
点\(\small{ \ \mathrm{P}(3, \ 5, \ 5) \ }\)から\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A}(1, \ 1, \ 1) \ }\)、\(\small{ \ \mathrm{B}(0, \ 3, \ 4) \ }\)、\(\small{ \ \mathrm{C}(-3, \ 4, \ 3) \ }\)が定める平面へ垂線を下ろす。このとき垂線の足\(\small{ \ \mathrm{H} \ }\)の座標を求めよ。
\(\small{ \ \mathrm{A}(1, \ 1, \ 1) \ }\)を通る平面の方程式は
\(\small{ \ a(x-1)+b(y-1)+c(z-1)=0 \ }\)
\(\small{ \ \mathrm{B}(0, \ 3, \ 4) \ }\)、\(\small{ \ \mathrm{C}(-3, \ 4, \ 3) \ }\)をそれぞれ代入すると
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
-a+2b+3c=0 \\
-4a+3b+2c=0\\
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて
\(\small{ \ b=2a, \ c=-a \ }\)
\(\small{ \ a(x-1)+2a(y-1)-a(z-1)=0 \ }\)
これを整理して
\(\small{ \ x+2y-z-2=0 \ }\)
この平面の法線ベクトルは\(\small{ \ (1, \ 2, \ -1) \ }\)
点\(\small{ \ \mathrm{P}(3, \ 5, \ 5) \ }\)を通り、この法線ベクトルに平行な直線上の点は
\(\small{\begin{eqnarray} \ (x, \ y, \ z)&=&(3, \ 5, \ 5)+t(1, \ 2, \ -1)\\
&=&(t+3, \ 2t+5, \ -t+5) \ \end{eqnarray}}\)
これが平面\(\small{ \ x+2y-z-2=0 \ }\)と交わるので
\(\small{ \ t+3+2(2t+5)-(-t+5)-2=0 \ }\)
\(\small{ \ 6t+6=0 \ }\)\(\small{ \ \therefore t=-1 \ }\)
よって交点の座標は\(\small{ \ (2, \ 3, \ 6) \ }\)

垂線の長さ
上の例題では点\(\small{ \ \mathrm{P}(3, \ 5, \ 5) \ }\)から\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A}(1, \ 1, \ 1) \ }\)、\(\small{ \ \mathrm{B}(0, \ 3, \ 4) \ }\)、\(\small{ \ \mathrm{C}(-3, \ 4, \ 3) \ }\)が定める平面へ垂線を下ろして、その垂線の足となる平面と垂線の交点の座標を求めたけど、この垂線と平面の交点を\(\small{ \ \mathrm{H} \ }\)とするとき、\(\small{ \ \mathrm{PH} \ }\)の長さを求めてみよう。
実際\(\small{ \ \mathrm{H} \ }\)の座標は\(\small{ \ \mathrm{H}(2, \ 3, \ 6) \ }\)だったから、
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{PH}}&=&\overrightarrow{\mathrm{OH}}-\overrightarrow{\mathrm{OP}}\\
&=&(2, \ 3, \ 6)-(3, \ 5, \ 5)\\
&=&(-1, \ -2, \ 1) \ \end{eqnarray}}\)
だから垂線の長さは\(\small{ \ \vert \overrightarrow{\mathrm{PH}}\vert \ }\)を求めればいいから
\(\small{ \ \vert \overrightarrow{\mathrm{PH}}\vert=\sqrt{(-1)^2+(-2)^2+1^2}=\sqrt{6} \ }\)になる。
でもこれって今\(\small{ \ \mathrm{H} \ }\)の座標が\(\small{ \ \mathrm{H}(2, \ 3, \ 6) \ }\)って簡単な整数だったから求める計算は簡単だったけど、\(\small{ \ \mathrm{H} \ }\)の座標が分数を含んだ座標だったら、まあまあ計算が面倒だよね。
だから垂線の長さを求めるときは、法線ベクトルを利用しよう。
法線ベクトルを\(\small{ \ t \ }\)倍した長さが垂線の長さになるんだ。
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OH}}&=&\overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{PH}}\\
&=&\overrightarrow{\mathrm{OP}}+t\overrightarrow{n} \ \end{eqnarray}}\)
\(\small{ \ \overrightarrow{n} \ }\)は垂線の方向ベクトル、つまり平面の法線ベクトルってことね。
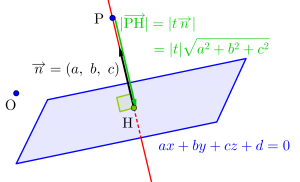
垂線の長さは\(\small{ \ \vert\overrightarrow{\mathrm{PH}}\vert \ }\)だから法線ベクトルを\(\small{ \ t \ }\)倍した\(\small{ \ \vert t\overrightarrow{n}\vert \ }\)が垂線の長さになるってこと。
上の例題だと法線ベクトルは\(\small{ \ (1, \ 2, \ -1) \ }\)で平面との交点は\(\small{ \ t=-1 \ }\)の時だったから垂線の長さは\(\small{ \ 1\times\vert\overrightarrow{n}\vert=\sqrt{6} \ }\)ってことになる。
\(\small{ \ \vert t\overrightarrow{n}\vert \ }\)は\(\small{ \ \vert t\vert \ \vert\overrightarrow{n}\vert \ }\)を計算すればいいから、\(\small{ \ t \ }\)が負の値だったときは正の値に変えて計算しよう。
\(\small{ \ t \ }\)が負の時は点\(\small{ \ \mathrm{P} \ }\)から平面に向かう方向と法線ベクトルの向きが逆だったってことになるだけだから、大きさは絶対値をとって正の値にして構わないからね。
このやり方だと\(\small{ \ t \ }\)が分数になることはあっても法線は整数のベクトルになるから、計算が楽だから覚えておこう。

Point 直線と平面の交点の求め方
①直線の方程式は媒介変数表示にして平面の方程式に代入する
②垂線の方向ベクトルは平面の法線ベクトルと同じ
③垂線の長さは法線ベクトルの長さの\(\small{ \ t \ }\)倍から求める

