こんにちは、リンス(@Lins016)です。
今回はメネラウスの定理の証明について学習していこう。
メネラウスの定理とその覚え方
メネラウスの定理
\(\small{ \ \triangle \mathrm{ABC} \ }\)を一つの直線で切るとき辺 \(\small{ \ \mathrm{BC}, \ }\)\(\small{ \ \mathrm{CA}, \ }\)\(\small{ \ \mathrm{AB} \ }\)またはその延長との交点を\(\small{ \ \mathrm{P, \ Q, \ R} \ }\)とすると
\(\small{ \ \mathrm{\displaystyle \frac{BP}{PC}\cdot \displaystyle \frac{CQ}{QA}\cdot \displaystyle \frac{AR}{RB}}=1 \ }\)
メネラウスの定理の逆
\(\small{ \ \triangle \mathrm{ABC} \ }\)の辺 \(\small{ \ \mathrm{BC}, \ }\)\(\small{ \ \mathrm{CA}, \ }\)\(\small{ \ \mathrm{AB} \ }\)またはその延長上の点を\(\small{ \ \mathrm{P, \ Q, \ R} \ }\)とするとき外分点の個数が奇数個で、かつ\(\small{ \ \mathrm{\displaystyle \frac{BP}{PC}\cdot \displaystyle \frac{CQ}{QA}\cdot \displaystyle \frac{AR}{RB}}=1 \ }\)が成り立つならば三点\(\small{ \ \mathrm{P, \ Q, \ R} \ }\)は同一直線上にある。
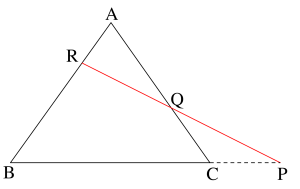
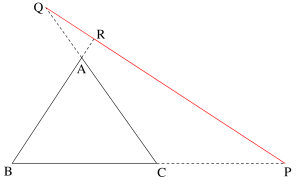
メネラウスの定理の証明
\(\small{ \ \triangle \mathrm{ABC} \ }\)の頂点\(\small{ \ \mathrm{C} \ }\)を通って直線\(\small{ \ \mathrm{PR} \ }\)に平行な直線と\(\small{ \ \mathrm{AB} \ }\)との交点を\(\small{ \ \mathrm{D} \ }\)とすると
\(\small{ \ \triangle \mathrm{BCD} \backsim \triangle \mathrm{BPQ} \ }\)より
\(\small{ \ \mathrm{BP:PC=BR:RD} \ }\)
\(\small{ \ \therefore \mathrm{\displaystyle \frac{BP}{PC}= \displaystyle \frac{BR}{RD}} \ }\)
また\(\small{ \ \triangle \mathrm{ARQ}\backsim \triangle \mathrm{ADC} \ }\)より
\(\small{ \ \mathrm{CQ:QA=DR:RA} \ }\)
\(\small{ \ \therefore \mathrm{\displaystyle \frac{CQ}{QA}= \displaystyle \frac{DR}{RA}} \ }\)
よって
\(\small{\mathrm{\displaystyle \frac{BP}{PC}\cdot \displaystyle \frac{CQ}{QA}\cdot \displaystyle \frac{AR}{RB}\\
=\displaystyle \frac{BR}{RD}\cdot \displaystyle \frac{DR}{RA}\cdot \displaystyle \frac{AR}{RB}}\\
=1 \ }\)

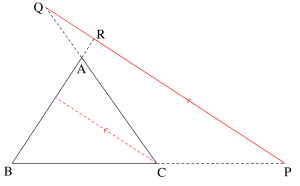
メネラウスの定理の逆の証明
\(\small{ \ \triangle \mathrm{ABC} \ }\)の辺 \(\small{ \ \mathrm{BC}, \ }\)\(\small{ \ \mathrm{CA}, \ }\)\(\small{ \ \mathrm{AB} \ }\)またはその延長上にある点を\(\small{ \ \mathrm{P, \ Q, \ R} \ }\)かつ\(\small{ \ \mathrm{\displaystyle \frac{BP}{PC}\cdot \displaystyle \frac{CQ}{QA}\cdot \displaystyle \frac{AR}{RB}}=1 \ }\)が成り立つとする。
また、このとき直線\(\small{ \ \mathrm{PR} \ }\)と直線\(\small{ \ \mathrm{AC} \ }\)との交点を\(\small{ \ \mathrm{Q'} \ }\)とする。
\(\small{ \ \mathrm{P, \ Q', \ R} \ }\)は同一直線上の点だから
メネラウスの定理より
\(\small{ \ \mathrm{\displaystyle \frac{BP}{PC}\cdot \displaystyle \frac{CQ'}{Q'A}\cdot \displaystyle \frac{AR}{RB}}=1 \ }\)が成り立つ。
仮定より
\(\small{ \ \mathrm{\displaystyle \frac{BP}{PC}\cdot \displaystyle \frac{CQ}{QA}\cdot \displaystyle \frac{AR}{RB}}=1 \ }\)
よって
\(\small{ \ \mathrm{\displaystyle \frac{CQ'}{Q'A}= \displaystyle \frac{CQ}{QA}} \ }\)より
点\(\small{ \ \mathrm{Q'} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)は同じ点である。
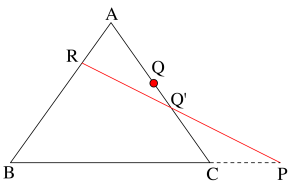
つまり\(\small{ \ \triangle \mathrm{ABC} \ }\)の辺 \(\small{ \ \mathrm{BC}, \ }\)\(\small{ \ \mathrm{CA}, \ }\)\(\small{ \ \mathrm{AB} \ }\)またはその延長上の点を\(\small{ \ \mathrm{P, \ Q, \ R} \ }\)とするとき外分点の個数が奇数個で、かつ\(\small{ \ \mathrm{\displaystyle \frac{BP}{PC}\cdot \displaystyle \frac{CQ}{QA}\cdot \displaystyle \frac{AR}{RB}}=1 \ }\)が成り立つならば三点\(\small{ \ \mathrm{P, \ Q, \ R} \ }\)は同一直線上にある。
メネラウスの定理の覚え方
まずはメネラウスの定理が利用できる三角形の形を覚えよう。
三角形の各辺またはその延長と一本の直線が交わっている図のような形の場合に利用できる。
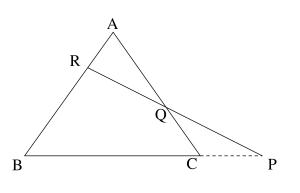
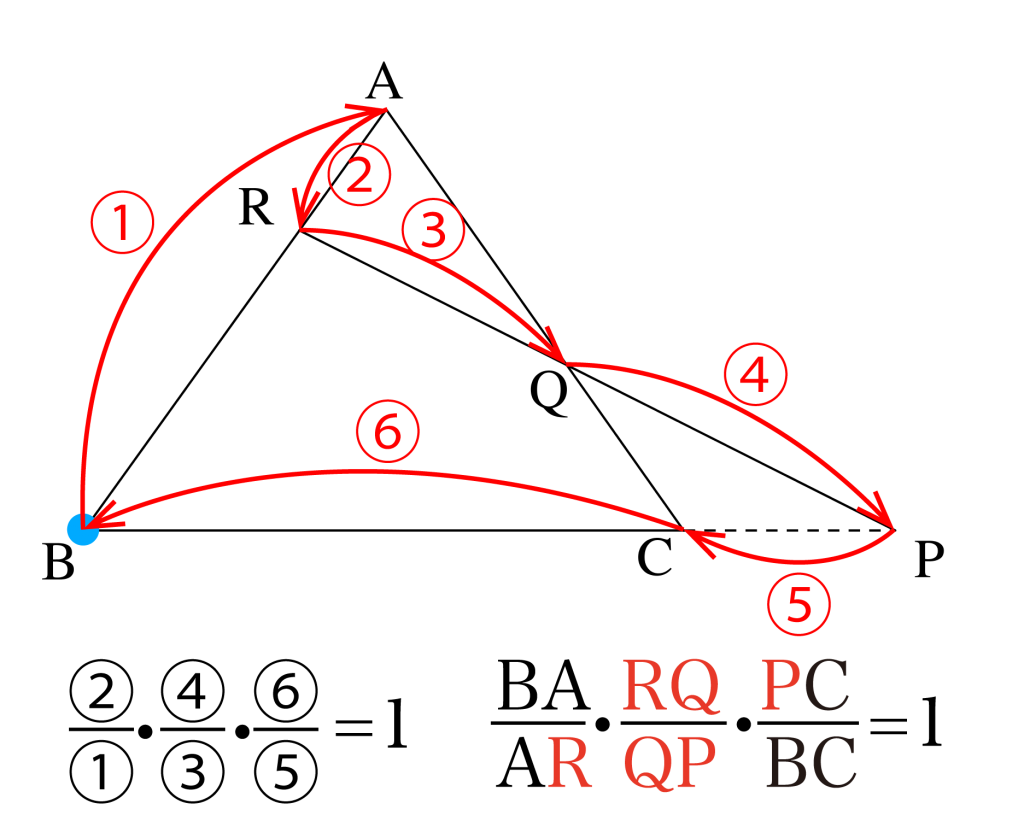
覚え方は下図のように三角形の頂点(この場合点\(\small{ \ \mathrm{B} \ }\))を始点と終点として三角形の頂点と三角形の辺(または辺の延長線)上の点を交互に結んだ線分の長さを順番に分数式に当てはめて覚えるのがいい。
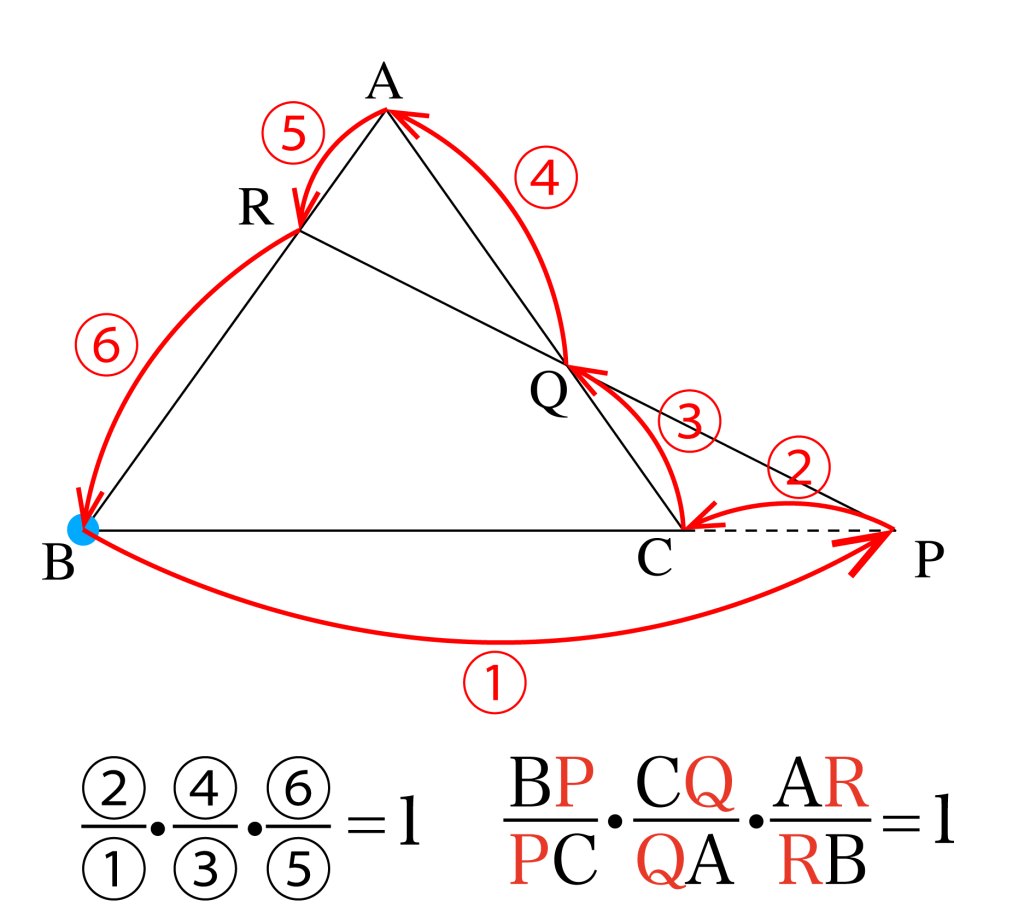
さらにこれを応用して、下図のように利用することもあるから覚えておこう。