こんにちは、リンス(@Lins016)です。
今回は三角形の内角の二等分線と線分比の証明について学習していこう。
三角形の内角の二等分線と線分比の証明
\(\small{ \ \triangle \mathrm{ABC} \ }\)の\(\small{ \ \angle \mathrm{A} \ }\)の二等分線と線分\(\small{ \ \mathrm{BC} \ }\)の交点を\(\small{ \ \mathrm{D} \ }\)とすると
\(\small{ \ \mathrm{AB}:\mathrm{AC}=\mathrm{BD}:\mathrm{CD} \ }\)

相似を利用した三角形の内角の二等分線と線分比の証明
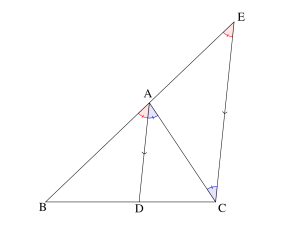
\(\small{ \ \mathrm{C} \ }\)を通り\(\small{ \ \mathrm{AD} \ }\)に平行な直線と直線\(\small{ \ \mathrm{AB} \ }\)との交点を\(\small{ \ \mathrm{E} \ }\)とすると、
\(\small{ \ \mathrm{AD} /\!/ \mathrm{CE} \ }\)より
\(\small{ \ \angle \mathrm{BAD}=\angle \mathrm{BEC} \ }\)(同位角)
\(\small{ \ \angle \mathrm{DAC}=\angle \mathrm{ACE} \ }\)(錯角)
\(\small{ \ \mathrm{AD} \ }\)は角の二等分線より
\(\small{ \ \angle \mathrm{BAD}=\angle \mathrm{DAC} \ }\)
\(\small{ \ \therefore \angle \mathrm{BEC}=\angle \mathrm{ACE} \ }\)
よって\(\small{ \ \triangle \mathrm{ACE} \ }\)は二等辺三角形
\(\small{ \ \mathrm{AC}=\mathrm{AE} \ }\)
\(\small{ \ \triangle \mathrm{ABD} \backsim \triangle \mathrm{EBC} \ }\)より
\(\small{ \ \mathrm{AB}:\mathrm{AE}=\mathrm{BD}:\mathrm{CD} \ }\)
\(\small{ \ \mathrm{AC}=\mathrm{AE} \ }\)より
\(\small{ \ \mathrm{AB}:\mathrm{AC}=\mathrm{BD}:\mathrm{CD} \ }\)
面積を利用した三角形の内角の二等分線と線分比の証明
高さが等しいので
\(\small{ \ \mathrm{BD}:\mathrm{CD}=\triangle \mathrm{ABD}:\mathrm{ACD} \ }\)
\(\small{ \ \triangle \mathrm{ABD}= \displaystyle \frac{1}{2} \mathrm{AB}\cdot \mathrm{AD} \sin \displaystyle \frac{\mathrm{A}}{2} \ }\)
\(\small{ \ \triangle \mathrm{ACD}= \displaystyle \frac{1}{2} \mathrm{AD}\cdot \mathrm{AC} \sin \displaystyle \frac{\mathrm{A}}{2} \ }\)
\(\small{ \ \triangle \mathrm{ABD}:\mathrm{ACD}=\mathrm{AB}: \mathrm{AC} \ }\)
よって\(\small{ \ \mathrm{AB}:\mathrm{AC}=\mathrm{BD}:\mathrm{CD} \ }\)


