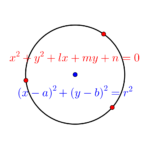こんにちは、リンス(@Lins016)です。
今回は二次関数の決定について学習していこう。
二次関数の決定
二次関数の決定とは与えられた情報(ヒント)から二次関数を求めることなんだけど、やり方を間違えると計算量が大変なことになったりするから、問題からのヒントによって解法を使い分けていこう。
・グラフ上の\(\small{ \ 3 \ }\)点が与えられている場合
\(\small{ \ y=ax^2+bx+c \ }\)の一般形に\(\small{ \ 3 \ }\)点を代入した連立方程式を解く
・頂点や軸に関するヒントが与えられている場合
\(\small{ \ y=a(x-p)^2+q \ }\)を利用する
\(\small{ \ y=a(x-p)^2+q \ }\)の平方形は\(\small{ \ a, \ p, \ q \ }\)を、\(\small{ \ y=ax^2+bx+c \ }\)の一般形は\(\small{ \ a, \ b, \ c \ }\)を求めれば二次関数が決定するよね。
二次関数を決定するには、平方形でも一般形でも\(\small{ \ 3 \ }\)つの文字を求めればいいから、どっちの式を利用しても大差なさそうだけど、そうじゃないから気をつけよう。
今回はどんなときに平方形や一般形を使い分けるのか、このあとの記事を読んでしっかりと理解しておこう。
一般形を利用した二次関数の決定
単純にグラフ上の\(\small{ \ 3 \ }\)点の座標が与えられていたら、\(\small{ \ y=ax^2+bx+c \ }\)の一般形に代入することで\(\small{ \ a, \ b, \ c \ }\)を含んだ\(\small{ \ 3 \ }\)つの式ができるから、その式を連立して解こう。
例えば\(\small{ \ (x, \ y)=(1, \ 2) \ }\)を一般形に代入すると\(\small{ \ 2=a+b+c \ }\)になるけど、これを一般形に代入すると\(\small{ \ 2=a(1-p)^2+q \ }\)ってなって展開すると式がひどいことになるのがわかるよね。
グラフ上の\(\small{ \ 3 \ }\)点が与えられている場合に平方形を利用するととんでもない計算量になるから、絶対に一般形に代入するようにしよう。
また、\(\small{ \ y=2x^2+x+3 \ }\)を平行移動したグラフがある\(\small{ \ 2 \ }\)点を通るといった問題も\(\small{ \ y=2x^2+bx+c \ }\)として一般形で解こう。平行移動は\(\small{ \ x^2 \ }\)の係数が変化しないんだったよね。忘れている人は下の二次関数の平行移動をもう一度学習しておこう。
-

二次関数のグラフの平行移動
平方形の移動と一般形の移動について詳しく解説しています。
続きを見る
平方形を利用した二次関数の決定
\(\small{ \ y=a(x-p)^2+q \ }\)の平方形は軸や頂点に関するヒントが与えられているときに利用するんだけど、むしろ「一般形を利用しない場合に平方系を利用する」って覚えておいた方が簡単だからそう覚えておこう。
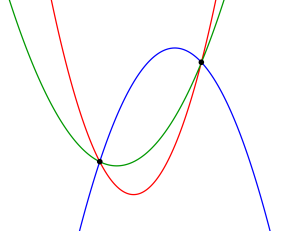
グラフ上の\(\small{ \ 3 \ }\)点が与えられている場合、一般形を利用したら二次関数が決定したよね。これって\(\small{ \ 3 \ }\)点が与えられているから決定するんだ。これが\(\small{ \ 2 \ }\)点だったら二次関数は決定しない。
だって図を見てもわかるけど、\(\small{ \ 2 \ }\)点を通る二次関数って複数あるよね。例えば\(\small{ \ 2 \ }\)点のうちの\(\small{ \ 1 \ }\)点が頂点だと二次関数は定まるけど、頂点じゃなければ定まらないんだ。このことをきちんと頭に入れておこう。
問題文から与えられているグラフ上の点が\(\small{ \ 2 \ }\)点以下だと二次関数は決定しないから、平行移動させたり、頂点や軸に関するヒントが問題文に入っている可能性がかなり高い。
だからグラフ上の\(\small{ \ 3 \ }\)点が与えられていない場合は平方形を利用することがほとんどなんだ。だから軸や頂点に関するヒントを見逃さないようにしよう。
\(\small{ \ a, \ p, \ q \ }\)のわからない文字を解くためには連立方程式を作らないといけないけど、平方形を利用する場合は代入する点の数が少ないから、「頂点の座標が\(\small{ \ y=2x+1 \ }\)上にある」みたいなヒントから\(\small{ \ (p, \ q)=(t, \ 2t+1) \ }\)のように求める文字の数を減らしてからグラフ上の点を代入していこう。
代入できる点の数と求める文字の数が同じじゃないと解けないから、通る点の数と同じ数の文字で二次関数を表すことから始めよう。
次の\(\small{ \ 2 \ }\)次関数を求めよ。
(1)\(\small{ \ (-1, \ 9), \ (1, \ -1), \ (2, \ 0) \ }\)を通る
(2)\(\small{ \ y=2x^2 \ }\)を平行移動したもので\(\small{ \ (1, \ 3) \ }\)を通り、頂点が\(\small{ \ y=2x-3 \ }\)上にある
(3)軸の方程式が\(\small{ \ x=3 \ }\)で\(\small{ \ (1, \ 1), \ (4, \ 2) \ }\)を通る
(4)\(\small{ \ (2, \ 0)(4, \ 0) \ }\)で\(\small{ \ x \ }\)軸と交わり、\(\small{ \ (0, \ -2) \ }\)で\(\small{ \ y \ }\)軸と交わる
(1)求める\(\small{ \ 2 \ }\)次関数を\(\small{ \ y=ax^2+bx+c \ }\)とおく
\(\small{ \ (-1, \ 9), \ (1, \ -1), (2, \ 0) \ }\)を通るので
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
9=a-b+c\\
-1=a+b+c\\
0=4a+2b+c
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=2, \ b=-5, \ c=2 \ }\)
よって\(\small{ \ y=2x^2-5x+2 \ }\)
(2)頂点の\(\small{ \ x \ }\)座標を\(\small{ \ t \ }\)とすると
頂点の座標は\(\small{ \ (t, \ 2t-3) \ }\)となり求める\(\small{ \ 2 \ }\)次関数は\(\small{ \ y=2(x-t)^2+2t-3 \ }\)とおける
これが\(\small{ \ (1, \ 3) \ }\)を通るので
\(\small{ \ 1=2(3-t)^2+2t-3 \ }\)
\(\small{ \ 2t^2-2t-4=0 \ }\)
\(\small{ \ (t+1)(t-2)=0 \ }\)
\(\small{ \ \therefore t=-1, \ 2 \ }\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y=2(x+1)^2-5\\
y=2(x-2)^2+1
\end{array}
\right.
\end{eqnarray} \ }\)
(3)求める\(\small{ \ 2 \ }\)次関数は\(\small{ \ y=a(x-3)^2+b \ }\)とおける
\(\small{ \ (1, \ 1), \ (4, \ -2) \ }\)を通るので
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
1=4a+b\\
-2=a+b
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=1, \ b=-3 \ }\)
よって\(\small{ \ y=(x-3)^2-3 \ }\)
(4)求める\(\small{ \ 2 \ }\)次関数は\(\small{ \ (2, \ 0), \ (4, \ 0) \ }\)を通るので
\(\small{ \ y=a(x-2)(x-4) \ }\)とおける
これが\(\small{ \ (0, \ -2) \ }\)を通るので
\(\small{ \ -2=8a \ }\)
\(\small{ \ \therefore a=-\displaystyle \frac{1}{4} \ }\)
よって\(\small{ \ y=-\displaystyle \frac{1}{4}(x-2)(x-4) \ }\)

(1)から(4)までの解答を見て分かる通り、グラフ上の点を代入すれば方程式が\(\small{ \ 1 \ }\)つできるよね。
代入する点の数と二次関数を表すために使っている未知数の数が同じじゃないと解けないから、点を代入するときには未知数の数と代入する点の数が同じ数になるように関数の式を工夫しておこう。
Point 二次関数の決定
①グラフ上の\(\small{ \ 3 \ }\)点が与えれているときは一般形で解く
②軸や頂点が絡む場合は平方形で解く
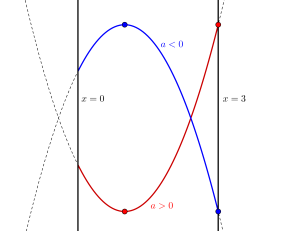
\(\small{ \ 2 \ }\)次関数\(\small{ \ f(x)=ax^2-2ax+b \ }\)(\(\small{ \ a, \ b \ }\)は定数)は区間\(\small{ \ 0\leqq x\leqq3 \ }\)における最大値が\(\small{ \ 3 \ }\)、最小値が\(\small{-5 \ }\)である。このとき\(\small{ \ a, \ b \ }\)の値を求めよ。
平方完成すると\(\small{ \ y=a(x-1)^2-a+b \ }\)
(i)\(\small{ \ a \gt0 \ }\)のとき
\(\small{ \ x=1 \ }\)のとき最小、\(\small{ \ x=3 \ }\)のとき最大になるので
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
-a+b=-5\\
3a+b=3
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=2, \ b=-3 \ }\)
(ii)\(\small{ \ a \lt0 \ }\)のとき
\(\small{ \ x=3 \ }\)のとき最小、\(\small{ \ x=1 \ }\)のとき最大になるので
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
3a+b=-5\\
-a+b=3
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=-2, \ b=1 \ }\)

円も中心や半径が絡むものと円周上の\(\small{ \ 3 \ }\)点が与えられているもので解き方が違うから、今回の二次関数の決定と本当によく似てるんだ。
-

円の方程式の決定
平方形と一般形を利用した円の方程式の求め方について詳しく解説しています。
続きを見る