こんにちは、リンス(@Lins016)です。
今回は接線の方程式について学習していこう。
接線の方程式は接点が重要
接線の方程式は接点がわかれば求めることができる。
だから接線の方程式の問題は接点を求める問題と認識しておこう。
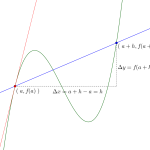
つまり、接点の座標を\(\small{ \ t \ }\)とおいて\(\small{ \ t \ }\)を求める問題ってことになるからね。前回学習した微分係数は接線の傾きを表すから、\(\small{ \ y=f(x) \ }\)上の点\(\small{ \ (t, \ f(t)) \ }\)における接線の傾きは\(\small{ \ x=t \ }\)における微分係数で\(\small{ \ f'(t) \ }\)になるから微分して微分係数を求めよう。
\(\small{ \ y=f(x) \ }\)上の
点\(\small{ \ (t, \ f(t)) \ }\)における接線の方程式
\(\small{ \ y=f'(t)(x-t)+f(t) \ }\)
-

微分係数と導関数
平均変化率、微分係数、導関数の違いについて詳しく解説しています。
続きを見る
曲線上の点における接線の方程式
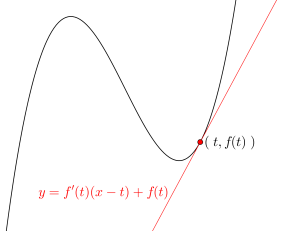
傾き\(\small{ \ m \ }\)で\(\small{ \ (a, \ b) \ }\)を通る直線の方程式は\(\small{ \ y=m(x-a)+b \ }\)と書ける。
これを曲線\(\small{ \ y=f(x) \ }\)上の点\(\small{ \ (t, \ f(t)) \ }\)における接線に利用してみると、傾き\(\small{ \ f'(t) \ }\)で\(\small{ \ (t, \ f(t)) \ }\)を通る直線の方程式は\(\small{ \ y=f'(t)(x-t)+f(t) \ }\)ってなるよね。
この式を\(\small{ \ (t, \ f(t)) \ }\)における接線の方程式としてきちんと覚えておこう。
曲線上にない点から引く接線の方程式
曲線\(\small{ \ y=f(x) \ }\)上にない点\(\small{ \ (a, \ b) \ }\)から引く接線の方程式を求める場合、接点の座標を\(\small{ \ (t, \ f(t)) \ }\)とおいて、この接点の座標を求めて接線の方程式を導こう。
接線の方程式を\(\small{ \ y=f'(t)(x-t)+f(t) \ }\)とすると、これを曲線上にない与えられた点\(\small{ \ (a, \ b) \ }\)が通るから代入して、\(\small{ \ t \ }\)の方程式\(\small{ \ b=f'(t)(a-t)+f(t) \ }\)を作ることができる。
この\(\small{ \ t \ }\)の方程式を解くことで、接点の\(\small{ \ x \ }\)座標を求めることができるんだ。
求めた接点の座標を接線の方程式に代入すると接線の方程式が求まるよね。
また、問題によっては曲線上の点が与えられる場合もある。曲線上の点だと安易に接点って思いがちだけど、曲線上の点から接線を引くこともできるから、接点と言われていない限りその点は接点じゃないかもしれないから注意して問題を解こう。
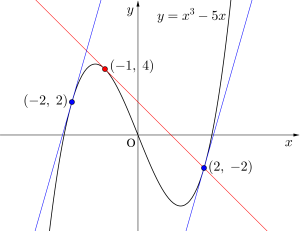
(1)曲線\(\small{ \ y=x^3-5x \ }\)上の点\(\small{ \ (-1,4) \ }\) における接線の方程式を求めよ。
(2)曲線\(\small{ \ y=x^3-5x \ }\)の接線の傾きが\(\small{ \ 7 \ }\)である接線の方程式を求めよ。
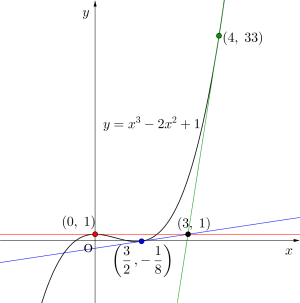
(3)点\(\small{ \ (3,1) \ }\)から曲線\(\small{ \ y=x^3-2x^2+1 \ }\)にひいた接線の方程式を求めよ。
(1)\(\small{ \ f(x)=x^3-5x \ }\)とすると求める方程式は
\(\small{\begin{eqnarray} \ y&=&f'(-1)(x+1)+f(-1)\\
&=&-2(x+1)+4\\
&=&-2x+2 \ \end{eqnarray}}\)
(2)\(\small{ \ f'(t)=7 \ }\)となる\(\small{ \ t \ }\)を求めれば良いので、\(\small{ \ 3t^2-5=7 \ \therefore t=\pm2\ }\)
よって求める方程式は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y=7(x-2)-2=7x-16\\
y=7(x+2)+2=7x+16
\end{array}
\right.
\end{eqnarray} \ }\)
(3)\(\small{ \ f(x)=x^3-2x^2+1 \ }\)とすると
\(\small{ \ (t,f(t)) \ }\)における接線の方程式は
\(\small{\begin{eqnarray} \ y&=&f'(t)(x-t)+f(t)\\
&=&(3t^2-4t)x-2t^3+2t^2+1 \ \end{eqnarray}}\)
これが\(\small{ \ (3,1) \ }\)を通るから
\(\small{ \ 1=3(3t^2-4t)-2t^3+2t^2+1 \ }\)
\(\small{ \ 2t^3-11t^2+12t=0 \ }\)
\(\small{ \ t(2t-3)(t-4)=0 \ }\)
\(\small{ \ t=0, \ \displaystyle \frac{3}{2}, \ 4 }\)
よって求める接線の方程式は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y=1\\
y=\displaystyle \frac{3}{4}x-\displaystyle \frac{5}{4}\\
y=32x-95
\end{array}
\right.
\end{eqnarray} \ }\)

Point 接線の方程式
①接線の方程式は接点の座標から求まる
②微分係数\(\small{ \ f'(t) \ }\)が接線の傾き
曲線\(\small{ \ y=x^3 \ }\)の原点以外の点\(\small{ \ \mathrm{P} \ }\)における接線が\(\small{ \ x \ }\)軸と交わる点を\(\small{ \ \mathrm{Q} \ }\)、\(\small{ \ y \ }\)軸と交わる点を\(\small{ \ \mathrm{R} \ }\)、再び曲線\(\small{ \ y=x^3 \ }\)と交わる点を\(\small{ \ \mathrm{S} \ }\)とするとき、\(\small{ \ \mathrm{PQ} \ }\)、\(\small{ \ \mathrm{QR} \ }\)、\(\small{ \ \mathrm{RS} \ }\)の比を求めよ。
接点の\(\small{ \ x \ }\)座標を\(\small{ \ t \ }\)とすると、
接線の方程式は \(\small{ \ y=3t^2(x-t)-t^3=3t^2x-2t^3 \ }\)
よって\(\small{ \ x \ }\)軸との交点の\(\small{ \ x \ }\)座標は
\(\small{ \ 3t^2x-2t^3=0 \ }\)
\(\small{ \ t\neq 0 \ }\)より\(\small{ \ x=\displaystyle \frac{2}{3}t \ }\)
また接線が曲線と交わる点の\(\small{ \ x \ }\)座標は
\(\small{ \ x^3=3t^2x-2t^3 \ }\)
\(\small{ \ x^3-3t^2x+2t^3=0 \ }\)
\(\small{ \ (x-t)^2(x+2t)=0 \ }\)
よって\(\small{ \ x=-2t \ }\)
線分の長さの比は\(\small{ \ x \ }\)座標の差の比と等しいから
\(\small{ \ \mathrm{PQ}:\mathrm{QR}:\mathrm{RS} =\displaystyle \frac{1}{3}t:\displaystyle \frac{2}{3}t:2t\\
=1:2:6 \ }\)


また、線分比は一直線上なら線分の長さ求めなくても、\(\small{ \ x \ }\)座標の差で相似比を求めればいいよね。面倒な三平方とかしないようにしよう。