こんにちは、リンス(@Lins016)です。
今回は定積分の計算と定積分の表す面積について学習していこう。
定積分の計算と面積
前回不定積分について学習しだけど、定期試験や入試で出題される積分の問題はほとんど定積分の問題なんだ。
今回はこの定積分がどんな値を表すのか詳しく考えてみよう。
・定積分の計算
\(\small{\begin{eqnarray} \ \displaystyle \int_{a }^{ b } f(x) dx&=&\left[ F(x) \right]_a^b\\
&=&F(b)-F(a) \ \end{eqnarray}}\)
・定積分の性質
①\(\small{ \ \displaystyle \int_{a}^{b} f(x) dx=-\displaystyle \int_{b}^{a} f(x) dx \ }\)
②\(\small{ \ \displaystyle \int_{a}^{a} f(x) dx=0 \ }\)
③\(\small{ \ \displaystyle \int_{a}^{b} f(x) dx=\displaystyle \int_{a}^{c} f(x) dx+\displaystyle \int_{c}^{a} f(x) dx \ }\)
定積分の計算
まずは定積分の計算について勉強していこう。
前回不定積分を教わったけど、定積分はこれに数値を代入して計算したものになる。
ただ\(\small{ \ f(x) \ }\)の原始関数\(\small{ \ F(x) \ }\)は無数にあって「\(\small{F(x)+}\)定数」の形で表されるから一つに定まらないけど、無数にあるのは定数部分の数が違うだけだから、\(\small{ \ x \ }\)に\(\small{ \ a, \ b \ }\)を代入した値の差\(\small{ \ F(b)-F(a) \ }\)の値はどの原始関数でも同じになるんだ。
例えば\(\small{ \ f(x)=2x \ }\)のとき、原始関数は\(\small{ \ F(x)=x^2+C \ }\)(\(\small{ \ C \ }\)は積分定数)になる。
この原始関数に\(\small{ \ a, \ b \ }\)を代入した値の差は
\(\small{\begin{eqnarray} \ F(b)-F(a)&=&(b^2+C)-(a^2+C)\\
&=&b^2-a^2 \ \end{eqnarray}}\)
になって積分定数\(\small{ \ C \ }\)の値によらないことがわかるよね。
この\(\small{ \ f(x) \ }\)の原始関数\(\small{ \ F(x) \ }\)に定義域内の\(\small{ \ a, \ b \ }\)を代入した\(\small{ \ F(b)-F(a) \ }\)を\(\small{ \ \displaystyle \int_{a }^{ b } f(x) dx \ }\)って書いて「\(\small{ \ f(x) \ }\)の\(\small{ \ a \ }\)から\(\small{ \ b \ }\)までの定積分」っていうからね。
\(\small{ \ F(b)-F(a) \ }\)を\(\small{ \ \begin{eqnarray}\left[ F(x) \right]_a^b \ \end{eqnarray}}\)って書くこともできるから
\(\small{\begin{eqnarray} \ \displaystyle \int_{a }^{ b } f(x) dx&=&\left[ F(x) \right]_a^b\\
&=&F(b)-F(a) \ \end{eqnarray}}\)
って計算しよう。
\(\small{ \ F(a), \ F(b) \ }\)の値の大きさによっては\(\small{ \ \displaystyle \int_{a }^{ b } f(x) dx \ }\)は正の値にも負の値にもなるからね。
次の値を求めよ。
(1)\(\small{ \ \displaystyle \int_{0 }^{ 1 } (-x^2+3x) dx \ }\)
(2)\(\small{ \ \displaystyle \int_{-1 }^{ 2 } (x+4)(x-2) dx \ }\)
(1)
= \left[ -\displaystyle\frac{1}{3}x^3+\displaystyle\frac{3}{2}x^2 \right]_0^1\\
=\left(-\displaystyle\frac{1}{3}\cdot1^3+\displaystyle\frac{3}{2}\cdot1^2\right)-\left(-\displaystyle\frac{1}{3}\cdot0^3+\displaystyle\frac{3}{2}\cdot0^2\right)\\
=\displaystyle\frac{7}{6} \ }\)
(2)
=\displaystyle \int_{-1 }^{ 2 } (x^2+2x-8) dx
= \left[ \displaystyle\frac{1}{3}x^3+x^2-8x \right]_{-1}^{2}\\
=\left(\displaystyle\frac{1}{3}\cdot2^3+2^2-8\cdot2\right)-\left\{\displaystyle\frac{1}{3}\cdot(-1)^3+(-1)^2-8(-1)\right)\\
=-18 \ }\)

まとめるなら\(\small{ \ \left[ 2x^3+x^2-8x \right]_{2}^{3} \ }\)を\(\small{ \ 2(3^3-2^3)+(3^2-2^2)-8(3-2) \ }\)って計算しないといけないから注意しよう。
定積分の値の意味
定積分の計算方法はわかったよね。
次にこの定積分で求めた値が何を表すかってことを考えてみよう。
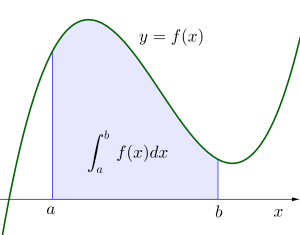
まず結論からいうと\(\small{ \ \displaystyle \int_{a }^{ b } f(x) dx \ }\)は\(\small{ \ y=f(x) \ }\)と\(\small{ \ x=a, \ x=b \ }\)と\(\small{ \ x \ }\)軸で囲まれた部分の面積を表すんだ。
ただ、\(\small{ \ y=f(x) \ }\)が\(\small{ \ x \ }\)軸より下にある面積はマイナスって定義しておこう。\(\small{ \ \displaystyle \int_{a }^{ b } f(x) dx \ }\)は負の値になることもあるからね。
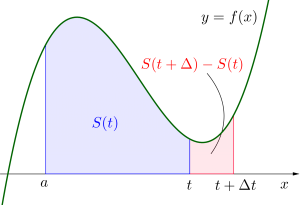
まずは\(\small{ \ y=f(x) \ }\)と\(\small{ \ x=a, \ x=t \ }\)と\(\small{ \ x \ }\)軸で囲まれた部分の面積を\(\small{ \ S(t) \ }\)としよう。
\(\small{ \ t \ }\)を\(\small{ \ \Delta t \ }\)増加させると面積は\(\small{ \ S(t) \ }\)から\(\small{ \ S(t+\Delta t) \ }\)に変化するから、その変化量は\(\small{ \ S(t+\Delta t)-S(t) \ }\)になるよね。
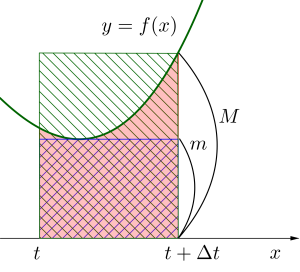
\(\small{ \ t\leqq x \leqq t+\Delta t \ }\)での\(\small{ \ f(x) \ }\)の最大値と最小値をそれぞれ\(\small{ \ M, \ m \ }\)とすると\(\small{ \ m\leqq f(x) \leqq M \ }\)になる。
これから図の斜線の二つの長方形の面積と\(\small{ \ y=f(x) \ }\)と\(\small{ \ x=t, \ x=t+\Delta t \ }\)と\(\small{ \ x \ }\)軸で囲まれた部分の面積を比較すると\(\small{ \ m\Delta t \leqq S(t+\Delta t)-S(t)\leqq M \Delta t \ }\)が言えるよね。
各辺を\(\small{ \ \Delta t \ }\)で割ると
\(\small{ \ m \leqq \displaystyle\frac{S(t+\Delta t)-S(t)}{\Delta t}\leqq M \ }\)
ここで\(\small{ \ \Delta t \to 0 \ }\)とすると、\(\small{ \ m, \ M \ }\)ともに\(\small{ \ f(t) \ }\)に近づく。
\(\small{ \ \displaystyle \lim_{ \Delta t \to 0 } \displaystyle\frac{S(t+\Delta t)-S(t)}{\Delta t}=S'(t) \ }\)だから\(\small{ \ S'(t)=f(t) \ }\)になる。
ちなみにこれは微分の定義を利用した式だから、忘れていたらもう一度復習しておこう。
\(\small{ \ S(t) \ }\)は\(\small{ \ S'(t) \ }\)を積分すればいいから
\(\small{\begin{eqnarray} \ S(t)&=&\displaystyle \int S'(t) dt\\
&=&\displaystyle \int f(t) dt\\
&=&F(t)+C \ \end{eqnarray}}\)
ただし\(\small{ \ C \ }\)は積分定数。
\(\small{ \ \therefore S(t)=F(t)+C \ }\)
\(\small{ \ S(a)=0 \ }\)だから\(\small{ \ C=-F(a) \ }\)
\(\small{ \ y=f(x) \ }\)と\(\small{ \ x=a, \ x=t \ }\)と\(\small{ \ x \ }\)軸で囲まれた部分の面積が\(\small{ \ S(t) \ }\)だから
\(\small{ \ S(t)=F(t)-F(a) \ }\)
つまり\(\small{ \ y=f(x) \ }\)と\(\small{ \ x=a, \ x=b \ }\)と\(\small{ \ x \ }\)軸で囲まれた部分の面積が\(\small{ \ S(b) \ }\)だから
\(\small{ \ S(b)=F(b)-F(a) \ }\)
これから\(\small{ \ y=f(x) \ }\)と\(\small{ \ x=a, \ x=b \ }\)と\(\small{ \ x \ }\)軸で囲まれた部分の面積は
\(\small{ \ S=\displaystyle \int_{a}^{b} f(x) dx \ }\)になるんだ。
定積分の性質
次に定積分の性質について学習していこう。
この三つの式は計算を楽にしたり、この後学習する定積分で表された関数でも利用したりするからしっかりと押さえておこう。
①\(\small{ \ \displaystyle \int_{a}^{b} f(x) dx=-\displaystyle \int_{b}^{a} f(x) dx \ }\)
\(\small{\begin{eqnarray} \ \displaystyle \int_{a}^{b} f(x) dx&=& \left[ F(x) \right]_a^b\\
&=&F(b)-F(a)\\
&=&-\left\{F(a)-F(b)\right\}\\
&=&- \left[ F(x) \right]_b^a\\
&=&-\displaystyle \int_{b}^{a} f(x) dx \ \end{eqnarray}}\)
②\(\small{ \ \displaystyle \int_{a}^{a} f(x) dx=0 \ }\)
\(\small{\begin{eqnarray} \ \displaystyle \int_{a}^{a} f(x) dx&=& \left[ F(x) \right]_a^a\\
&=&F(a)-F(a)\\
&=&0 \ \end{eqnarray}}\)
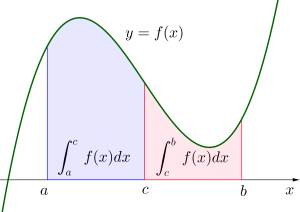
③\(\small{ \ \displaystyle \int_{a}^{b} f(x) dx=\displaystyle \int_{a}^{c} f(x) dx+\displaystyle \int_{c}^{a} f(x) dx \ }\)
定積分の値が面積を表すってことがわかってるから成り立つのがわかるよね。
次の定積分の値を求めよ。
積分する関数が同じものに注意すると
=\displaystyle \int_{-1}^{0} (3x^2-2x+5) dx+\displaystyle \int_{-1}^{0} (2x-3) dx\\
=\displaystyle \int_{-1}^{0} (3x^2-2) dx\\
=\left[ x^3-2x \right]_{-1}^{0}\\
=0-\left\{(-1)^3-2(-1)\right\}\\
=1 \ }\)

Point 定積分の計算と定積分の表す面積
①定積分の計算方法をマスターする
②定積分の表す値が何か知る
③定積分の性質の計算をマスターする

