こんにちは、リンス(@Lins016)です。
今回は偶関数・奇関数の定積分について学習していきましょう。
偶関数・奇関数の定積分の計算
偶関数とは\(\small{ \ y \ }\)軸について対称な関数で、奇関数とは原点について対称な関数だったよね。
これは三角関数を学習したときに出てきたと思うんだけど、今回はこれを積分に応用しようってことなんだけど、まずは偶関数・奇関数のことをもう一度復習しておこう。
\(\small{ \ \begin{eqnarray}
\displaystyle\int_{-a}^{a}x^n dx
=
\begin{cases}
2\displaystyle\int_{0}^{a}x^n dx&(n=2k)\\
\ \ \ 0&(n=2k-1)
\end{cases}
\end{eqnarray} \ }\)
・偶関数の場合

・奇関数の場合
計算を楽にする定積分
今回学習するのは計算を簡単にする積分なんだけど、その計算がいつ使えるのかってところから話をするね。
いつ使えるのかというと「積分の下端と上端の絶対値が等しいとき」なんだ。
つまり\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx \ }\)のとき。
だからこれから積分の計算をするときに\(\small{ \ \displaystyle\int_{-1}^{1}f(x) dx \ }\)や\(\small{ \ \displaystyle\int_{-3}^{3}f(x) dx \ }\)のような積分だったときは今から学習する計算方法を必ず利用するようにしよう。
ちなみに\(\small{ \ \displaystyle\int_{-1}^{2}f(x) dx \ }\)や\(\small{ \ \displaystyle\int_{-3}^{4}f(x) dx \ }\)のように積分の下端と上端の絶対値が等しくない場合は使えないからね。
偶関数と積分
偶関数とは\(\small{ \ y \ }\)軸について対称な関数のことで\(\small{ \ f(x)=f(-x) \ }\)を満たす関数のことだったよね。
特に数学Ⅱの積分法で出題される偶関数は\(\small{ \ x^n \ }\)の\(\small{ \ n \ }\)が偶数だと偶関数になるんだ。
偶関数同士を足したり引いたりしても偶関数だから、\(\small{ \ y=x^4+x^2 \ }\)も偶関数だからね。
それじゃ偶関数の積分\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx \ }\)を考えてみよう。
\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx \ }\)は積分の性質より
\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx=\displaystyle\int_{-a}^{0}f(x) dx+\displaystyle\int_{0}^{a}f(x) dx \ }\)
に分解することができるよね。
ここで\(\small{ \ y \ }\)軸について対称だから
\(\small{ \ \displaystyle\int_{-a}^{0}f(x) dx=\displaystyle\int_{0}^{a}f(x) dx \ }\)
つまり\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx=2\displaystyle\int_{0}^{a}f(x) dx \ }\)になる。
これは図を見ても明らかだよね。

実際\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx \ }\)を計算しても構わないんだけど\(\small{ \ 2\displaystyle\int_{0}^{a}f(x) dx \ }\)は下端が\(\small{ \ 0 \ }\)だから計算しなくていいんだ。
そのまま計算すると\(\small{ \ x \ }\)の偶数乗を積分して、\(\small{ \ -a \ }\)の値を代入して更に引くって作業になるけど、\(\small{ \ 0 \ }\)を代入する場合、その計算をする必要がなくなるから絶対使ったほうがいいよね。
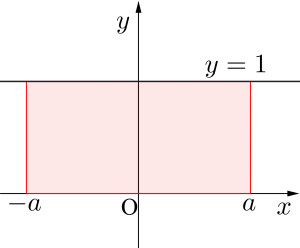
ちなみに\(\small{ \ y=1 \ }\)も\(\small{ \ y \ }\)軸に対称だから偶関数と同じ扱いができるからね。
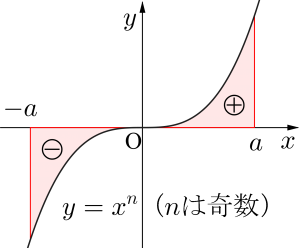
奇関数と積分
奇関数とは原点について対称な関数のことで\(\small{ \ f(-x)=-f(x) \ }\)を満たす関数のことだったよね。
特に数学Ⅱの積分法で出題される奇関数は\(\small{ \ x^n \ }\)の\(\small{ \ n \ }\)が奇数だと奇関数になるんだ。
奇関数同士を足したり引いたりしても奇関数だから、\(\small{ \ y=x^3+x \ }\)も奇関数だからね。
それじゃ奇関数の積分\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx \ }\)を考えてみよう。
\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx \ }\)は積分の性質より
\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx=\displaystyle\int_{-a}^{0}f(x) dx+\displaystyle\int_{0}^{a}f(x) dx \ }\)
に分解することができるよね。
ここで原点について対称だから、面積は同じ大きさだけど、符号が逆になるよね。
\(\small{ \ -\displaystyle\int_{-a}^{0}f(x) dx=\displaystyle\int_{0}^{a}f(x) dx \ }\)
つまり\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx=0 \ }\)になる。
これは図を見ても明らかだよね。

実際\(\small{ \ \displaystyle\int_{-a}^{a}f(x) dx \ }\)を計算しても構わないんだけど、どうぜ\(\small{ \ 0 \ }\)になるから計算する必要ないよね。
偶関数・奇関数と積分
下端と上端の絶対値が等しい定積分は偶関数と奇関数なら計算が簡単になることがわかったけど、偶関数と奇関数なんてめったに出題されたりしないよね。
でも整関数の項を一つ一つ分けたら偶関数奇関数の定積分を利用することができるんだ。
例えば\(\small{ \ \displaystyle\int_{-a}^{a}(2x^3-3x^2+x+1) dx \ }\)の場合
\(\small{ \ \displaystyle\int_{-a}^{a}(2x^3-3x^2+x+1) dx\\
=2\displaystyle\int_{-a}^{a}x^3 dx-3\displaystyle\int_{-a}^{a}x^2 dx+\displaystyle\int_{-a}^{a}x dx +\displaystyle\int_{-a}^{a} dx\\
=-2\cdot3\displaystyle\int_{0}^{a}x^2 dx+2\displaystyle\int_{-a}^{a} dx\\ \ }\)
\(\small{ \ y=2x^3-3x^2+x+1 \ }\)は偶関数でも奇関数でもないけど、一つずつの項にわけると偶関数奇関数の定積分が利用できるんだ。
だから計算する場合、奇関数の部分はどうせ\(\small{ \ 0 \ }\)になるから消しちゃって構わない。
\(\small{ \ \displaystyle\int_{-a}^{a}(2x^3-3x^2+x+1) dx\\
=2\displaystyle\int_{0}^{a}(-3x^2+1) dx \ }\)
って偶関数だけ残して二倍するようにしよう。
下端と上端の絶対値が等しい定積分を見たら必ずこの計算をするように心がけよう。
次の定積分の値を求めよ。
\(\small{ \ \displaystyle \int_{-1}^{1} (x^4+x^3+3x^2-2x+5) dx \ }\)
\(\small{ \ \displaystyle \int_{-1}^{1} (x^4+x^3+3x^2-2x+5) dx\\
=2\displaystyle \int_{0}^{1} (x^4+3x^2+5) dx\\
=2\left[\displaystyle\frac{1}{5}x^5+x^3+5x\right]_{0}^{1}\\
=\displaystyle\frac{62}{5} \ }\)

必ず積分する前に偶関数・奇関数に分けて奇関数を消して偶関数だけ残して二倍しよう。
Point 偶関数・奇関数の定積分
①積分区間の上端と下端の絶対値が等しいときの計算をマスターする

