こんにちは、リンス(@Lins016)です。
今回は通過領域について学習していこう。
通過領域とは?
突然通過領域って言われても困るよね。どんなものかというと
「実数\(\small{ \ t \ }\)の値が変化するとき、直線\(\small{ \ y=2tx+t^2 \ }\)の通過する領域を図示せよ。」っていうような、ある定数の値を変化させて直線や曲線が移動し、平面上を通過する部分を通過領域っていうんだ。
でも通過領域の問題はあまり定期テストは出題されない。っていうのも\(\small{ \ t \ }\)が実数全体を動くときの問題はすごく簡単に解けるし、\(\small{ \ t \ }\)に範囲があると難易度が上がりすぎて解くのにだいぶ時間もかかるからね。
だからこそ受験生は確実におさえといてほしいけど、まだこの図形と方程式の単元を学習したばっかりって生徒は\(\small{ \ t \ }\)が実数全体を動くときの解き方を理解しておけば、とりあえずは問題ないと思う。
だけどせっかくこのページを見るんだから、範囲がある問題もできるようにしてほしいってのが本当のところ。だって結局はいつかできるようにしないといけないんだもんね。
実数\(\small{ \ t \ }\)の値が変化するとき、直線\(\small{ \ y=2tx-t^2 \ }\)の通過する領域

通過領域の解き方
通過領域の問題には\(\small{ \ 2 \ }\)つの解き方がある。逆手流(逆像法)ってよばれる解法と、変数を\(\small{ \ 1 \ }\)つ固定する\(\small{ \ 1 \ }\)文字固定法だ。
ただ、\(\small{ \ 1 \ }\)文字固定法だとうまく計算がややこしかったり、うまくできない問題もあるから、逆手流の方法をしっかりと覚えておこう。
逆手流・逆像法
\(\small{ \ t \ }\)の値が変化するとき、\(\small{ \ y=2tx-t^2 \ }\)が通過する領域について考えてみよう。
\(\small{ \ y=2tx-t^2 \ }\)が\(\small{ \ (1, \ 1) \ }\)を通過するとすると、\(\small{ \ (1, \ 1) \ }\)を直線に代入して\(\small{ \ t=1 \ }\)になるよね。つまり\(\small{ \ y=2x-1 \ }\)のとき\(\small{ \ (1, \ 1) \ }\)を通過するって言える。
次に\(\small{ \ (0, \ 2) \ }\)を通過するとすると、\(\small{ \ (0, \ 2) \ }\)を直線に代入して\(\small{ \ -t^2=2 \ }\)になるから実数\(\small{ \ t \ }\)は存在しないことになる。つまりどんな\(\small{ \ t \ }\)の値を代入しても\(\small{ \ y=2tx-t^2 \ }\)の直線は\(\small{ \ (0, \ 2) \ }\)を通過しないってことになるんだ。
この考え方から直線が点\(\small{ \ (x, \ y) \ }\)を通過するとき、実数\(\small{ \ t \ }\)が存在すればいいから、\(\small{ \ y=2tx-t^2 \ }\)を\(\small{ \ t^2-2xt+y=0 \ }\)に変形して、この\(\small{ \ t \ }\)の二次方程式が解を持つ\(\small{ \ x, \ y \ }\)の条件こそが通過する領域をということになるんだ。
\(\small{ \ t \ }\)が実数をとるっていうのは\(\small{ \ t \ }\)の二次方程式の判別式が\(\small{ \ 0 \ }\)以上であればいいから、判別式\(\small{ \ D=(-2x)^2-4y \geqq0 \ }\)より求める領域は\(\small{ \ y \leqq x^2 \ }\)になる。
この方法を逆手流、または逆像法っていうんだ。

-

二次方程式の解の存在範囲(解の配置)
解の存在範囲について学習します。解がある値より大きい場合や二つの値の間にある場合など、複数の場合について解説しています。
続きを見る
1文字固定法
\(\small{ \ y=2tx-t^2 \ }\)に\(\small{ \ x=1 \ }\)を代入すると\(\small{ \ y=2t-t^2=-(t-1)^2+1 \ }\)になるよね。これは\(\small{ \ y-t \ }\)の関数とみると\(\small{ \ y\leqq1 \ }\)になる。つまり\(\small{ \ x=1 \ }\)のとき、領域は\(\small{ \ y \leqq 1 \ }\)になる。
これを\(\small{ \ x \ }\)のまま考えてみると、\(\small{ \ y=-(t-x)^2+x^2 \ }\)になるから、\(\small{ \ y\leqq x^2 \ }\)になるよね。
つまり\(\small{ \ x \ }\)が固定されているとすると、\(\small{ \ y \ }\)がどのような値をとるかを考えることで領域を導くんだ。
この方法を\(\small{ \ 1 \ }\)文字固定法っていうんだ
(1)\(\small{ \ t \ }\)が実数全体を動くとき、直線\(\small{ \ y=tx+t^2 \ }\)が通過する領域を図示せよ。
(2)\(\small{ \ t \ }\)が\(\small{ \ t\geqq -1 \ }\)を動くとき、直線\(\small{ \ y=tx+t^2 \ }\)が通過する領域を図示せよ。
(1)\(\small{ \ y=tx+t^2 \ }\)を変形して
\(\small{ \ t^2+tx-y=0 \ }\)
これが実数解を持てばいいいから
\(\small{ \ D=x^2+4y \geqq 0 \ }\)
\(\small{ \ y \geqq -\displaystyle \frac{1}{4}x^2 \ }\)
よって求める領域は図の斜線部分になる

(2)\(\small{ \ y=tx+t^2 \ }\)を変形して
\(\small{ \ t^2+tx-y=0 \ }\)
これが\(\small{ \ t\geqq -1 \ }\)で少なくとも\(\small{ \ 1 \ }\)つ実数解を持てばいいいから
\(\small{ \ f(t)=t^2+xt-y \ }\)とおくと
\(\small{ \ f(t)=\left(t+\displaystyle \frac{1}{2}x\right)^2-\displaystyle \frac{1}{4}x^2-y \ }\)より
(i)\(\small{ \ -\displaystyle \frac{1}{2}x \geqq -1 \ }\)\(\small{ \ \therefore x\leqq 2 \ }\)のとき
\(\small{ \ D=x^2+4y \geqq 0 \ }\)
\(\small{ \ y \geqq -\displaystyle \frac{1}{4}x^2 \ }\)
(ii)\(\small{ \ -\displaystyle \frac{1}{2}x \lt -1 \ }\)\(\small{ \ \therefore x\gt 2 \ }\)のとき
\(\small{ \ f(-1)\leqq 0 \ }\)
\(\small{ \ 1-x-y\leqq 0 \ }\)
(i)(ii)より求める領域は図の斜線部分になる
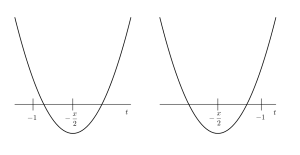

(1)\(\small{ \ y=tx+t^2 \ }\)を変形して
\(\small{ \ y=\left(t+\displaystyle \frac{1}{2}x^2\right)^2-\displaystyle \frac{1}{4}x^2 \ }\)
\(\small{ \ \therefore y \geqq -\displaystyle \frac{1}{4}x^2 \ }\)
よって求める領域は図の斜線部分になる

(2)\(\small{ \ y=tx+t^2 \ }\)を変形して
\(\small{ \ y=\left(t+\displaystyle \frac{1}{2}x\right)^2-\displaystyle \frac{1}{4}x^2=f(t) \ }\)とする
(i)\(\small{ -\ \displaystyle \frac{1}{2}x \geqq -1 \ }\)\(\small{ \ \therefore x\leqq 2 \ }\)のとき
\(\small{ \ y \geqq f(-\displaystyle \frac{1}{2}x) \ }\)
\(\small{ \ \therefore y \geqq -\displaystyle \frac{1}{4}x^2 \ }\)
(ii)\(\small{ \ -\displaystyle \frac{1}{2}x \lt -1 \ }\)\(\small{ \ \therefore x\gt 2 \ }\)のとき
\(\small{ \ y \geqq f(-1) \ }\)
\(\small{ \ y \geqq 1-x \ }\)
(i)(ii)より求める領域は図の斜線部分になる
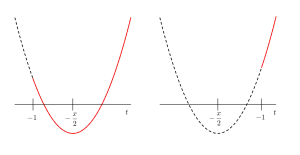


Point 直線や曲線の通過する領域
①通過領域の問題は逆手流(逆像法)か1文字固定のどちらかを利用しよう。
放物線\(\small{ \ y=x^2 \ }\)上の点\(\small{ \ P \ }\)を中心とし\(\small{ \ x \ }\)軸に接する円を考える。
\(\small{ \ P \ }\)が\(\small{ \ x \gt 0 \ }\)の範囲を動くとき、この円が通過する領域を求め、図示せよ。
(1)\(\small{ \ P (t, \ t^2)\ }\)とおく。
円の方程式は\(\small{ \ (x-t)^2+(y-t^2)^2=t^4 \ }\)
これを整理して
\(\small{ \ (2y-1)t^2+2xt-x^2-y^2=0 \ }\)
これが \(\small{ \ t \geqq 0 \ }\)に少なくとも1つの解を持てばよい
\(\small{ \ f(t)=(2y-1)t^2+2xt-x^2-y^2 \ }\)とすると
(i)\(\small{ \ 2y-1\gt 0 \ \therefore y \gt \displaystyle \frac{1}{2} \ }\)のとき
\(\small{ \ y=f(t) \ }\)のグラフは下に凸だから\(\small{ \ f(0) \lt 0 \ }\)であればよい。
\(\small{ \ f(0)=-x^2-y^2 \ }\)よりこれは常に成り立つ。
(ii)\(\small{ \ 2y-1=0 \ \therefore y=\displaystyle \frac{1}{2} \ }\)のとき
\(\small{ \ f(t)=2xt-x^2-\displaystyle \frac{1}{4} \ }\)となり
\(\small{ \ y=f(t) \ }\)は直線になる
\(\small{ \ f(0)=-x^2-\displaystyle \frac{1}{4}\lt 0 \ }\)より
\(\small{ \ t\gt 0 \ }\)で\(\small{ \ f(t)=0 \ }\)となるには傾き\(\small{ \ 2x \gt 0 \ }\)であればよい
よって\(\small{ \ x\gt 0 \ }\)
(iii)\(\small{ \ 2y-1\lt 0 \ \therefore y \lt \displaystyle \frac{1}{2} \ }\)のとき
\(\small{ \ y=f(t \ }\))の軸の方程式は\(\small{ \ t=\displaystyle \frac{-x}{2y-1} \ }\)
a)\(\small{ \ \displaystyle \frac{-x}{2y-1} \leqq 0 \ \therefore x \leqq 0 \ }\)のとき
\(\small{ \ f(0)\gt 0 \ }\)であればよい
\(\small{ \ f(0)=-x^2-y^2 \lt 0 \ }\)より不適
b)\(\small{ \ \displaystyle \frac{-x}{2y-1} \gt 0 \ \therefore x \gt 0 \ }\)のとき
\(\small{ \ f(t)=0 \ }\)の判別式\(\small{ \ D \geqq 0 \ }\)であればよい
\(\small{\begin{eqnarray} \ \displaystyle \frac{D}{4}&=&x^2+(2y-1)(x^2+y^2)\\
&=&2y\left(x^2+y^2-\displaystyle \frac{1}{2}y \right) \geqq 0\end{eqnarray}\ }\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y\geqq0\\
x^2+y^2-\displaystyle \frac{1}{2}y \geqq 0
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ \therefore x^2+\left(y-\displaystyle \frac{1}{4}\right)^2\geqq\displaystyle \frac{1}{4} \ }\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y\leqq0\\
x^2+y^2-\displaystyle \frac{1}{2}y \leqq 0
\end{array}
\right.
\end{eqnarray} \ }\)
これを満たす\(\small{ \ x, \ y\ }\)は存在しない
(i)〜(iii)より求める領域は図の斜線部分になる。