こんにちは、リンス(@Lins016)です。
今回は円のベクトル方程式について学習していこう。
円のベクトル方程式と円の接線のベクトル方程式
今回はベクトル方程式で円の方程式や円の接線の方程式について考えていくんだけど、成分表示の問題にして考えると図形と方程式の円の方程式や円の接線と同じ式を求めることになるから、合わせて図形と方程式も復習しておこう。
中心\(\small{ \ \mathrm{A}\left(\overrightarrow{ a }\right) \ }\)、半径\(\small{ \ r \ }\)の円のベクトル方程式
\(\small{ \ \left| \overrightarrow{ p }- \overrightarrow{ a }\right|=r \ }\)
点\(\small{ \ \mathrm{A}\left( \overrightarrow{ a }\right) \ }\)と点\(\small{ \ \mathrm{B}\left( \overrightarrow{ b }\right) \ }\)を直径とする円のベクトル方程式
\(\small{ \ \left(\overrightarrow{ p }- \overrightarrow{ a }\right)\cdot \left( \overrightarrow{ p }- \overrightarrow{ b }\right)=0 \ }\)
中心\(\small{ \ \mathrm{C}\left( \overrightarrow{ c }\right) \ }\)、接点を\(\small{ \ \mathrm{P_0}\left( \overrightarrow{ p_0 }\right) \ }\)円の接線のベクトル方程式
\(\small{ \ \left(\overrightarrow{ p }- \overrightarrow{ c }\right)\cdot \left(\overrightarrow{ p_0 }- \overrightarrow{ c }\right)=r^2 \ }\)
中心と半径が与えられている円のベクトル方程式
円は中心と半径が分かっていたら書けるよね。
ベクトル方程式を利用する場合も同じで中心が点\(\small{ \ \mathrm{A}\left(\overrightarrow{ a }\right) \ }\)、半径が\(\small{ \ r \ }\)の円周上にある点\(\small{ \ \mathrm{P}\left(\overrightarrow{ p }\right) \ }\)のベクトル方程式は
\(\small{ \ \left|\overrightarrow{ \mathrm{AP} }\right|=r \ }\)
\(\small{ \ \therefore \left| \overrightarrow{ p }- \overrightarrow{ a }\right|=r \ }\)になる。
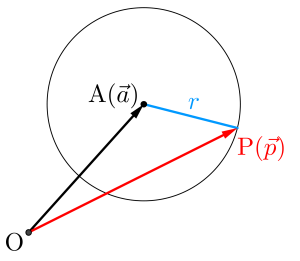
この式をさらに変形すると
\(\small{ \ \left| \overrightarrow{ p }- \overrightarrow{ a }\right|^2=\left(\overrightarrow{ p }- \overrightarrow{ a }\right)\cdot\left(\overrightarrow{ p }- \overrightarrow{ a }\right) \ }\)より
\(\small{ \ \left(\overrightarrow{ p }- \overrightarrow{ a }\right)\cdot\left(\overrightarrow{ p }- \overrightarrow{ a }\right)=r^2 \ }\)ともかけるからね。
また成分表示の問題の場合\(\small{ \ \overrightarrow{ p }=(x, \ y) \ }\)、\(\small{ \ \overrightarrow{ a }=(a_1, \ a_2) \ }\)とすると
\(\small{ \ \overrightarrow{ p }- \overrightarrow{ a }=(x-a_1, \ y-a_2) \ }\)になるから
\(\small{ \ \left|\overrightarrow{ p }- \overrightarrow{ a }\right|= \sqrt{(x-a_1)^2+(y-a_2)^2} \ }\)
\(\small{ \ \left| \overrightarrow{ p }- \overrightarrow{ a }\right|^2=r^2 \ }\)より
\(\small{ \ (x-a_1)^2+(y-a_2)^2=r^2 \ }\)になって図形と方程式で勉強した円の方程式と同じになることがわかるよね。
二点ABを直径とする円のベクトル方程式
点\(\small{ \ \mathrm{A}\left( \overrightarrow{ a }\right) \ }\)と点\(\small{ \ \mathrm{B}\left( \overrightarrow{ b }\right) \ }\)を直径とする円周上にある点\(\small{ \ \mathrm{P}\left( \overrightarrow{ p }\right) \ }\)のベクトル方程式は
\(\small{ \ \mathrm{AP \perp BP} \ }\)から
\(\small{ \ \overrightarrow{ \mathrm{AP} }\cdot \overrightarrow{ \mathrm{BP} }=0 \ }\)
になる。
つまり
\(\small{ \ \left(\overrightarrow{ p }- \overrightarrow{ a }\right)\cdot \left( \overrightarrow{ p }- \overrightarrow{ b }\right)=0 \ }\)になるんだ。
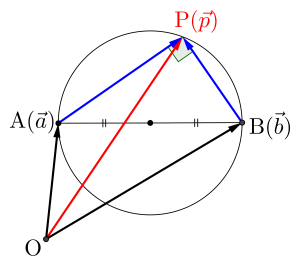
点\(\small{ \ \mathrm{P} \ }\)が点\(\small{ \ \mathrm{A} \ }\)や点\(\small{ \ \mathrm{B} \ }\)と一致するときでも\(\small{ \ \overrightarrow{ p }- \overrightarrow{ a }=0 \ }\)または\(\small{ \ \overrightarrow{ p }- \overrightarrow{ b }=0 \ }\)になるから成り立つからね。
次の円の方程式をベクトルを用いて求めよ。
(1)点\(\small{ \ \mathrm{C}(3, \ 2) \ }\)が中心で点\(\small{ \ \mathrm{R}(1, \ 1) \ }\)を通る円
(2)点\(\small{ \ \mathrm{A}(2, \ 5) \ }\)と点\(\small{ \ \mathrm{B}(4, \ 1) \ }\)を直径の両端とする円
(1)\(\small{ \ \mathrm{P}(x, \ y) \ }\)とすると
\(\small{ \ \left| \overrightarrow{ \mathrm{CP} }\right|= \left| \overrightarrow{ \mathrm{CR} }\right| \ }\)
\(\small{ \ \left| \overrightarrow{ \mathrm{OP} }- \overrightarrow{ \mathrm{OC} }\right|= \left| \overrightarrow{ \mathrm{OR} }- \overrightarrow{ \mathrm{OC} }\right| \ }\)
\(\small{ \ \sqrt{(x-3)^2+(y-2)^2}= \sqrt{5} \ }\)
\(\small{ \ \therefore (x-3)^2+(y-2)^2=5 \ }\)
(2)\(\small{ \ \mathrm{P}(x, \ y) \ }\)とすると
\(\small{ \ \overrightarrow{ \mathrm{AP} }\cdot \overrightarrow{ \mathrm{BP} }=0 \ }\)
\(\small{ \ \left(\overrightarrow{ \mathrm{OP} }- \overrightarrow{ \mathrm{OA} }\right)\cdot \left( \overrightarrow{ \mathrm{OP} }- \overrightarrow{ \mathrm{OB} }\right)=0 \ }\)
\(\small{ \ (x-2, \ y-5)\cdot(x-4, \ y-1)=0 \ }\)
\(\small{ \ x^2-6x+y^2-6y+13=0 \ }\)
\(\small{ \ \therefore (x-3)^2+(y-3)^2=5 \ }\)

円の接線のベクトル方程式
円の接線のベクトル方程式について考えてみよう。
円の中心を点\(\small{ \ \mathrm{C}\left( \overrightarrow{ c }\right) \ }\)、円周上の接点を\(\small{ \ \mathrm{P_0}\left( \overrightarrow{ p_0 }\right) \ }\)とすると、接線上の点\(\small{ \ \mathrm{P}\left( \overrightarrow{ p }\right) \ }\)の位置ベクトルは
\(\small{ \ \overrightarrow{ \mathrm{P_0P} } \cdot \overrightarrow{ \mathrm{CP_0} }=0 \ }\)
\(\small{ \ \left(\overrightarrow{ p }- \overrightarrow{ p_0 }\right)\cdot \left(\overrightarrow{ p_0 }-\overrightarrow{ c } \right)=0 \ }\)になる。
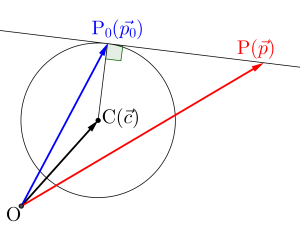
また図より
\(\small{ \ \left| \overrightarrow{ \mathrm{CP} }\right|\cos \theta= \left| \overrightarrow{ \mathrm{CP_0} }\right| \ }\)
両辺に\(\small{ \ \left| \overrightarrow{ \mathrm{CP_0} }\right| \ }\)をかけると
\(\small{ \ \left| \overrightarrow{ \mathrm{CP} }\right|\left| \overrightarrow{ \mathrm{CP_0} }\right|\cos \theta= \left| \overrightarrow{ \mathrm{CP_0} }\right|^2 \ }\)
\(\small{ \ \overrightarrow{ \mathrm{CP} }\cdot \overrightarrow{ \mathrm{CP_0} }=r^2 \ }\)
\(\small{ \ \therefore \left(\overrightarrow{ p }- \overrightarrow{ c }\right)\cdot \left(\overrightarrow{ p_0 }- \overrightarrow{ c }\right)=r^2 \ }\)
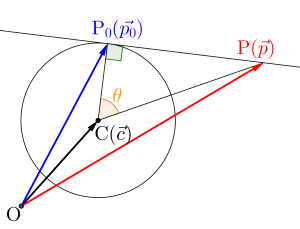
これは
\left(\overrightarrow{ p }- \overrightarrow{ c }+ \overrightarrow{ c }- \overrightarrow{ p_0 }\right)\cdot \left(\overrightarrow{ p_0 }-\overrightarrow{ c } \right)=0 \ }\)
展開して移行すると
&=& \left|\overrightarrow{ p_0 }-\overrightarrow{ c }\right|^2\\
&=&r^2 \ \end{eqnarray}}\)
として導くこともできるからね。
点\(\small{ \ \mathrm{P} \ }\)の位置ベクトルを\(\small{ \ \mathrm{P}\left(\overrightarrow{ p }\right)=(x, \ y) \ }\)、円の中心\(\small{ \ \mathrm{C} \ }\)の位置ベクトルを\(\small{ \ \mathrm{C}\left(\overrightarrow{ c }\right)=(a, \ b) \ }\)接点\(\small{ \ P_0 \ }\)の位置ベクトルを\(\small{ \ \mathrm{P_0}\left(\overrightarrow{ p_0 }\right)=(x_0, \ y_0) \ }\)とすると
\(\small{ \ \left(\overrightarrow{ p }- \overrightarrow{ c }\right)\cdot \left(\overrightarrow{ p_0 }- \overrightarrow{ c }\right)=r^2 \ }\)
\(\small{ \ (x-a, \ y-b)\cdot(x_0-a, \ y_0-b)=r^2 \ }\)
これは円の接線の方程式を表してるよね。
中心\(\small{ \ (1, \ 1) \ }\)、半径\(\small{ \ \sqrt{2} \ }\)の円に\(\small{ \ (2, \ 2) \ }\)で接する接線の方程式をベクトルを用いて求めよ。
\(\small{ \ \overrightarrow{ \mathrm{OC} }=(1, \ 1) \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OA} }=(2, \ 2) \ }\)、\(\small{ \ \mathrm{OP}=(x, \ y) \ }\)
とすると
\(\small{ \ \overrightarrow{ \mathrm{AP} }\cdot \overrightarrow{ \mathrm{AC} }=0 \ }\)
\(\small{ \ (x-2, \ y-2)\cdot(1, \ 1)=0 \ }\)
\(\small{ \ \therefore x+y-4=0 \ }\)
Point 円のベクトル方程式
①円のベクトル方程式と図形と方程式の円の方程式をリンクさせよう
②図形からベクトル方程式を導こう

