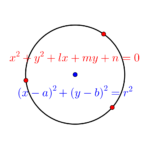こんにちは、リンス(@Lins016)です。
今回は円の方程式について学習していこう。
円の方程式は2パターン
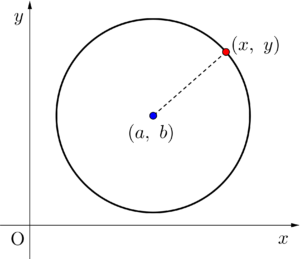
円って、ある点(円の中心)から等しい距離にある点の集まり(集合)だよね。
ある点を\(\small{ \ (a,b) \ }\)、円周上の点を\(\small{ \ (x,y) \ }\)、この二点の距離を\(\small{ \ r \ }\)とすると、\(\small{\sqrt{(x-a)^2+(y-b)^2}=r \ }\)の式が成り立つ。
これを二乗した\(\small{(x-a)^2+(y-b)^2=r^2 \ }\)が、円の方程式になるんだ。
さらにこの式を展開して、文字を置き換えて整理したのが \(\small{ \ x^2+y^2+lx+my+n=0 \ }\)で一般形の円の方程式になるんだ。でも、\(\small{l^2+m^2-4n\gt0 \ }\)じゃないと円の方程式にはならないから気をつけよう。
・平方形
中心\(\small{ \ (a,b) \ }\)・半径\(\small{ \ r \ }\)
\(\small{(x-a)^2+(y-b)^2=r^2}\)
・一般形
\(\small{x^2+y^2+lx+my+n=0}\)
円の方程式は中心と半径で表される平方形と、平方形を展開した一般形の二通りの表し方があるから、問題によって使い分けていくことが重要になるんだ。
それぞれいつ使うのか、パターンをしっかりと理解しよう。
平方形と一般形の円の方程式
円の方程式は\(\small{ \ (x-a)^2+(y-b)^2=r^2 \ }\)と\(\small{ \ x^2+y^2+lx+my+n=0 \ }\)の\(\small{ \ 2 \ }\)つの形があるけど、図を書くときは、円の中心の座標と半径がわかってないと書けないよね。だから円の方程式は平方形で書く方がいい。
だけど円の方程式を求める場合は、平方形だと大変な場合もあるから、円の方程式を求める場合は、どっちの形を使えばいいか与えられた条件から使い分けないといけない。それについては下の記事を確認しておこう。
-

円の方程式の決定
平方形と一般形を利用した円の方程式の求め方について詳しく解説しています。
続きを見る
円の方程式の成立条件
\(\small{x^2+y^2+lx+my+n=0 \ }\)だからといって円の方程式にならない場合もあるからね。
\(\small{l^2+m^2-4n\gt0 \ }\)を満たして初めて円の方程式って言えるんだ。それは\(\small{ \ (x-a)^2+(y-b)^2=R \ }\)の\(\small{ \ R \ }\)が\(\small{ \ 0 \ }\)以下の数だと半径が存在しないことになるから円にならないよね。
つまり\(\small{ \ x^2 \ }\)や\(\small{ \ y^2 \ }\)の項があるからといって円の方程式ってことにはならないから注意しよう。
次の方程式はどのような図形を表すか答えなさい。
(1)\(\small{x^2+y^2-6x-4y+12=0}\)
(2)\(\small{x^2+y^2-6x-4y+13=0}\)
(3)\(\small{x^2+y^2-6x-4y+14=0}\)
(1) \(\small{x^2+y^2-6x-4y+12=0}\)
\(\small{(x-3)^2+(y-2)^2=1}\)より
中心\(\small{(3,2)}\)、半径\(\small{1}\)の円
(2) \(\small{x^2+y^2-6x-4y+13=0}\)
\(\small{(x-3)^2+(y-2)^2=0}\)より
平面上にある点\(\small{(3,2)}\)
(3) \(\small{x^2+y^2-6x-4y+14=0}\)
\(\small{(x-3)^2+(y-2)^2=-1}\)
(左辺)>\(\small{0 \ }\)、(右辺)\(\small{=-1 \ }\)より
与えられた式を満たす点は存在しない。


今回は小問だから\(\small{ \ l^2+m^2-4n \ }\)を計算してもいいけど、大問の中で出題されたら、どうせ中心と半径求めることになるだろうから二度手間だもんね。平方形のとき、半径を示す右辺が正の数だと円、\(\small{ \ 0 \ }\)だと点、負の数だと存在しないってことになるからね。
Point 円の方程式
①円の成立条件に注意しよう
②基本的には平方形を利用して円の中心、半径を求めよう
方程式\(\small{ \ x^2+y^2+2kx-4ky+10k-20=0 \ }\)の表す図形\(\small{ \ C \ }\)について考える。ただし、\(\small{ \ k \ }\)は実数とする。
(1)図形\(\small{ \ C \ }\)は円であることを示せ。
(2)\(\small{ \ k \ }\)はどのような値であっても定点を通る。その定点の座標を求めよ。
(3)図形\(\small{ \ C \ }\)で囲まれる部分の面積の最小値を求めよ。
(1)図形\(\small{ \ C \ }\)の方程式を変形すると、
\(\small{ \ (x+k)^2+(y-2k)^2=5k^2-10k+20 \ }\)
ここで
\(\small{ \ 5k^2-10k+20=5(k-1)^2+15 \gt 0 \ }\)
よって図形\(\small{ \ C \ }\)は中心\(\small{ \ (-k、2k) \ }\)、半径\(\small{ \ \sqrt{5k^2-10k+20} \ }\)の円である。
(2)図形\(\small{ \ C \ }\)の方程式を\(\small{ \ k \ }\)について整理すると
\(\small{ \ x^2+y^2-20+k(2x-4k+10)=0 \ }\)
これが\(\small{ \ k \ }\)についての恒等式になればよいので
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
x^2+y^2-20=0\cdots①\\
2x-4k+10=0\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{②}\)より\(\small{ \ x=2y-5 \ }\)
これを\(\small{①}\)に代入して、\(\small{ \ (2y-5)^2+y^2=20 \ }\)
\(\small{ \ y^2-4y+1=0 \ }\)
\(\small{ \ \therefore y=2\pm \sqrt{3} \ }\)
このとき\(\small{ \ x=2(2\pm \sqrt{3})-5 \ }\)
\(\small{ \ \therefore x=-1\pm \sqrt{3} \ }\)
よって求める座標は
\(\small{ \ (-1+ \sqrt{3}、2+ \sqrt{3})、(-1- \sqrt{3}、2- \sqrt{3}) \ }\)
(3)(1)より半径が最小になるのは\(\small{ \ k=1 \ }\)のときで\(\small{ \ r=\sqrt{15} \ }\)
よって求める面積は\(\small{ \ \pi r^2=15\pi \ }\)