ベクトルの内積とその利用方法

こんにちは、リンス(@Lins016)です。
今回はベクトルの内積とその利用方法について学習していこう。

ベクトルの内積とは？

ベクトルの内積とは$\small{ \ \overrightarrow{ a }\cdot \overrightarrow{ b }=| \overrightarrow{ a }|| \overrightarrow{ b }|\cos \theta \ }$で定義された値。

ベクトルは大きさと向きをもつものだったけど、この内積は定義された式を見てもわかるけど、スカラー量（大きさ）になるから、$\small{ \ \overrightarrow{ a }+\overrightarrow{ a }\cdot \overrightarrow{ b } \ }$のようなベクトルとスカラーを足したりする計算式にはならないから注意しよう。

ベクトルの内積の意味

内積の意味に詳しく触れている教科書はないと思う。

それは内積が$\small{ \ \overrightarrow{ a }\cdot \overrightarrow{ b }=|\overrightarrow{ a }||\overrightarrow{ b }|\cos\theta \ }$で定義された意味を考えても試験や入試ではほとんど問われることはないからなんだ。

内積の定義について考えると非常に難しくなるから、腑に落ちないかもしれないけど$\small{ \ \overrightarrow{ a }\cdot \overrightarrow{ b }=|\overrightarrow{ a }||\overrightarrow{ b }|\cos\theta \ }$で定義された値だってことだけ受け入れておこう。

図的には$\small{ \ \overrightarrow{ b } \ }$の$\small{ \ \overrightarrow{ a } \ }$方向成分の大きさと$\small{ \ \overrightarrow{ a } \ }$の大きさを掛け合わせたものってことなんだけど、その値が図のどこの大きさを表すかってのはわからないだよね。

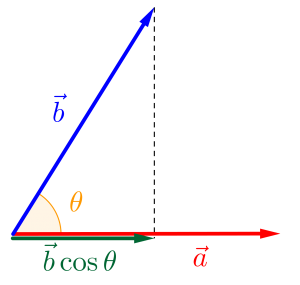
ただ、この後説明する内積がなぜ必要なのかってことをしっかり学習して覚えてほしい。

ベクトルの内積とベクトルの大きさ

次の図のベクトルを確認してみよう。
この青いベクトル$\small{ \ \overrightarrow{ p } \ }$はどちらも$\small{ \ \overrightarrow{ p }=\overrightarrow{ a }+\overrightarrow{ b } \ }$を満たすベクトルになる。

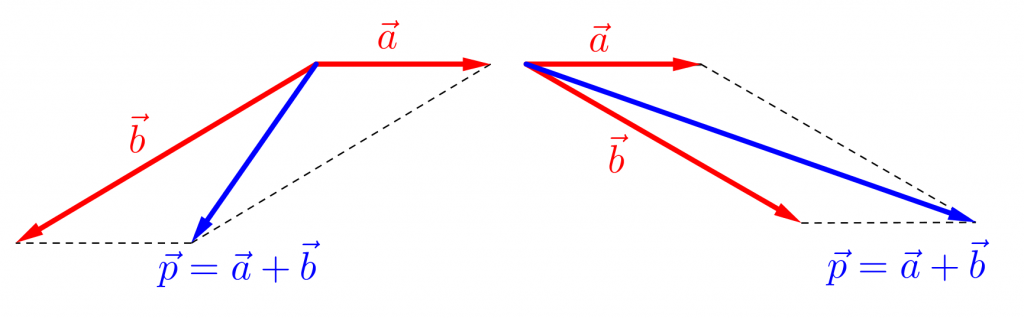
どっちの図も$\small{ \ |\overrightarrow{ a }|=1, \ |\overrightarrow{ b }|=2 \ }$だけど、明らかに$\small{ \ \overrightarrow{ p } \ }$の長さ（つまり$\small{ \ |\overrightarrow{ p }| \ }$）が違う。

でも二つの図は$\small{ \ \overrightarrow{ a } \ }$と$\small{ \ \overrightarrow{b } \ }$の長さは同じだから、違うのは$\small{ \ \overrightarrow{ a } \ }$と$\small{ \ \overrightarrow{ b } \ }$のなす角だけだよね。

つまりなす角によって$\small{ \ \overrightarrow{ a }+\overrightarrow{ b } \ }$の大きさは変化するってことがわかる。

$\small{ \ \overrightarrow{ p } \ }$の大きさは
$\small{\begin{eqnarray} \ |\overrightarrow{ p }|^2&=&\overrightarrow{ p }\cdot \overrightarrow{ p }\\ &=&( \overrightarrow{ a }+ \overrightarrow{ b })\cdot( \overrightarrow{ a }+ \overrightarrow{ b })\\ &=&\overrightarrow{ a }\cdot \overrightarrow{ a }+\overrightarrow{ a }\cdot \overrightarrow{ b }+\overrightarrow{ b }\cdot \overrightarrow{ a }+ \overrightarrow{ b }\cdot \overrightarrow{ b }\\ &=&| \overrightarrow{ a }|^2+2\overrightarrow{ a }\cdot \overrightarrow{ b }+| \overrightarrow{ b }|^2 \ \end{eqnarray}}$
になる。

$\small{ \ | \overrightarrow{ a }|=1, \ |\overrightarrow{ b }|=2 \ }$だから$\small{ \ \overrightarrow{ a } \ }$と$\small{ \ \overrightarrow{ b } \ }$のなす角を$\small{ \ \theta \ }$とすると$\small{ \ | \overrightarrow{ p }|^2=5+2\cos \theta \ }$になる。

だからなす角が変化することで$\small{ \ | \overrightarrow{ p }| \ }$の値が変化することがわかる。

つまり$\small{ \ \overrightarrow{ p } \ }$の大きさを求めるためにはなす角（内積）が必要になるんだ。

ベクトルの大きさの求め方

ベクトルの基本で「平面ベクトルは二つの基準のベクトルでその他のベクトル表す」ってことを話したとおもうけど、平面ベクトルでは二つのベクトル$\small{ \ \overrightarrow{ \mathrm{OA} } \ }$と$\small{ \ \overrightarrow{ \mathrm{OB} } \ }$を基準とするとその他のベクトルを
$\small{ \ \overrightarrow{ \mathrm{OP} }=s\overrightarrow{ \mathrm{OA} }+t \overrightarrow{ \mathrm{OB} } \ }$で表すことができる。

だから$\small{ \ \overrightarrow{ \mathrm{OP} } \ }$の大きさを求める場合は
$\small{ \ |\overrightarrow{ \mathrm{OP} }|^2=|s \overrightarrow{ \mathrm{OA}}+t \overrightarrow{ \mathrm{OB} }|^2\\ =s^2| \overrightarrow{ \mathrm{OA} }|^2+2st \overrightarrow{ \mathrm{OA} }\cdot \overrightarrow{ \mathrm{OB} }+t^2| \overrightarrow{ \mathrm{OB} }|^2 \ }$
を計算すれば求めることができる。

$\small{ \ s, \ t \ }$は位置を表す係数になるから、二つの基準のベクトルの大きさとなす角を（内積）が与えられていればすべてのベクトルの大きさを調べることができるんだ。

逆にいえば二つの基準のベクトルの大きさとなす角が与えられていなければ大きさを求めることはできないからね。

内積の考え方のまとめ

結局高校数学の範囲では内積が何を表すものかっていうのは知らなくても問題ない。
だけど内積を使えば何が求まる（できる）のかってことは知っておこう。

ほとんどのベクトルの問題は基準のベクトルが与えられて、そこから問いが始まる。
基準のベクトルの内積が与えられていないと内分や外分の位置を求める問題になるけど、
基準のベクトルの内積が与えられていると他のベクトルの大きさや、他のベクトルのなす角とかも求めることができる。

つまり問題の幅が広がるんだ。

内積を利用できるかできないかっていうのは問題文でわかるから、基準のベクトルの大きさと角度や内積が与えられているか確認しよう。

問題文に大きさが与えられている問題は内積が与えられていなくても内積を求めることができるかもしれないって思っておこう。

大きさは内分や外分の比として使われることもあるけど、内積を求めるために使うこともあるからね。

Point ベクトルの内積とその利用方法

①ベクトルの内積の定義の式を覚えよう
②$\small{ \ |\overrightarrow{\mathrm{OA}}| \ }$、$\small{ \ |\overrightarrow{\mathrm{OB}}| \ }$、$\small{ \ \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} \ }$の値を求めて、その他のベクトルの大きさを求めよう

問題解答

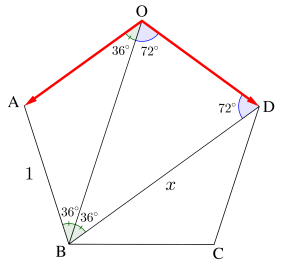
$\small{ \ 1 \ }$辺の長さが$\small{ \ 1 \ }$の正五角形$\small{ \ \mathrm{OABCD} \ }$に対して、$\small{ \ \overrightarrow{a}=\overrightarrow{\mathrm{OA}} \ }$、$\small{ \ \overrightarrow{b}=\overrightarrow{\mathrm{OD}} \ }$とおく。$\small{ \ \mathrm{BD} \ }$の長さを$\small{ \ x \ }$とするとき次の問いに答えよ。
(1)$\small{ \ \overrightarrow{\mathrm{OB}} \ }$と$\small{ \ \overrightarrow{\mathrm{AB}} \ }$を$\small{ \ \overrightarrow{a} \ }$と$\small{ \ \overrightarrow{b} \ }$と$\small{ \ x \ }$を用いて表せ。
(2)内積$\small{ \ \overrightarrow{a}\cdot \overrightarrow{b} \ }$の値を$\small{ \ x \ }$を用いて表せ。
(3)$\small{ \ x \ }$の値を求めよ。
(4)$\small{ \ \cos72^{\circ} \ }$の値を求めよ。

(1)正五角形$\small{ \ \mathrm{OABCD} \ }$は同一円周上にあるから円周角の関係より

$\small{ \ \angle \mathrm{AOB}=\angle \mathrm{OBD}=36^{\circ} \ }$
よって$\small{ \ \mathrm{AO}/\!/ \mathrm{BD} \ }$
$\small{ \ |\overrightarrow{\mathrm{OA}}|=1 \ }$、$\small{ \ |\overrightarrow{\mathrm{BD}}|=x \ }$
$\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OB}}&=&\overrightarrow{\mathrm{OD}}+\overrightarrow{\mathrm{DB}}\\ &=&\overrightarrow{b}+x\overrightarrow{\mathrm{OA}}\\ &=&x\overrightarrow{a}+\overrightarrow{b} \ \end{eqnarray}}$
$\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AB}}&=&\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\\ &=&(x\overrightarrow{a}+\overrightarrow{b})-\overrightarrow{a}\\ &=&(x-1)\overrightarrow{a}+\overrightarrow{b} \ \end{eqnarray}}$

(2)
$\small{\begin{eqnarray} \ |\overrightarrow{\mathrm{AB}}|^2&=&|(x-1)\overrightarrow{a}+\overrightarrow{b}|^2\\ &=&(x-1)^2|\overrightarrow{a}|^2+2(x-1)\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2 \ \end{eqnarray}}$
$\small{ \ 1=(x-1)^2+2(x-1)\overrightarrow{a}\cdot\overrightarrow{b}+1 \ }$
$\small{ \ x\gt1 \ }$より
$\small{ \ \overrightarrow{a}\cdot\overrightarrow{b}=\displaystyle \frac{-x+1}{2}\cdots① \ }$

(3)
$\small{\begin{eqnarray} \ |\overrightarrow{\mathrm{OB}}|^2&=&|x\overrightarrow{a}+\overrightarrow{b}|^2\\ &=&x^2|\overrightarrow{a}|^2+2x\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2 \ \end{eqnarray}}$
$\small{ \ |\overrightarrow{\mathrm{OB}}|=|\overrightarrow{\mathrm{BD}}|=x \ }$より
$\small{ \ x^2=x^2+2x\overrightarrow{a}\cdot\overrightarrow{b}+1 \ }$
$\small{ \ \therefore \overrightarrow{a}\cdot \overrightarrow{b}=-\displaystyle \frac{1}{2x}\cdots② \ }$
$\small{ \ ①② \ }$より
$\small{ \ \displaystyle \frac{-x+1}{2}=-\displaystyle \frac{1}{2x} \ }$
$\small{ \ x^2-x-1=0 \ }$
$\small{ \ x\gt 0 \ }$より$\small{ \ x=\displaystyle \frac{1+\sqrt{5}}{2} \ }$

(4)
(3)より
$\small{ \ \overrightarrow{a}\cdot\overrightarrow{b}=\displaystyle \frac{1-\sqrt{5}}{4} \ }$
また、
$\small{\begin{eqnarray} \ \overrightarrow{a}\cdot\overrightarrow{b}&=&|\overrightarrow{a}||\overrightarrow{b}|\cos 108^{\circ}\\ &=&\cos 108^{\circ}\\ &=&-\cos72^{\circ} \ \end{eqnarray}}$
よって$\small{ \ \cos72^{\circ}=\displaystyle \frac{\sqrt{5}-1}{4} \ }$