こんにちは、リンス(@Lins016)です。
今回はヘロンの公式の証明について学習していこう。
ヘロンの公式
三角形\(\small{ \ \mathrm{ABC} \ }\)の面積を\(\small{ \ \mathrm{S} \ }\)とすると
\(\small{ \ \mathrm{S}=\sqrt{s(s-a)(s-b)(s-c)} \ }\)
ただし、\(\small{ \ s=\displaystyle \frac{a+b+c}{2} \ }\)
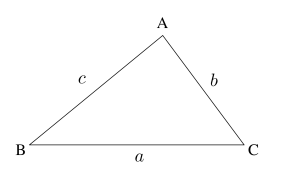
三角形\(\small{ \ \mathrm{ABC} \ }\)の面積を\(\small{ \ \mathrm{S} \ }\)とすると
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle \frac{1}{2}bc\sin \mathrm{A}\\[16pt]
&=&\displaystyle \frac{1}{2}bc \sqrt{1-\cos^2 \mathrm{A}}\\[16pt]
&=&\displaystyle \frac{1}{2}bc \sqrt{1-\left(\displaystyle \frac{b^2+c^2-a^2}{2bc}\right)^2}\\[16pt]
&=&\displaystyle \frac{1}{2}\sqrt{b^2c^2-\displaystyle \frac{(b^2+c^2-a^2)^2}{4}}\\[16pt]
&=&\displaystyle \frac{1}{4}\sqrt{4b^2c^2-(b^2+c^2-a^2)^2}\cdots①\\[16pt]
&=&\displaystyle \frac{1}{4}\sqrt{(2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2)}\\[16pt]
&=&\displaystyle \frac{1}{4}\sqrt{\left\{(b+c)^2-a^2\right\}\left\{a^2-(b-c)^2\right\}}\\[16pt]
&=&\displaystyle \frac{1}{4}\sqrt{(a+b+c)(b+c-a)(a-b+c)(a+b-c)}\\[16pt]
&=&\sqrt{\displaystyle \frac{a+b+c}{2}\cdot \displaystyle \frac{b+c-a}{2} \cdot \displaystyle \frac{a-b+c}{2} \cdot \displaystyle \frac{a+b-c}{2}}\\[16pt]
&=&\sqrt{\displaystyle \frac{a+b+c}{2}\left(\displaystyle \frac{a+b+c}{2}-a\right)\left(\displaystyle \frac{a+b+c}{2}-b\right)\left(\displaystyle \frac{a+b+c}{2}-c\right)}\\[16pt]
&=&\sqrt{s(s-a)(s-b)(s-c)} \ \end{eqnarray}}\)
ただし、辺の長さが無理数を含んでいる場合、\(\small{ \ s \ }\)も無理数になり、計算が複雑になるので、\(\small{① \ }\)の式を展開して
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle \frac{1}{4}\sqrt{4b^2c^2-(b^2+c^2-a^2)^2}\cdots①\\[12pt]
&=&\displaystyle \frac{1}{4}\sqrt{2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)} \ \end{eqnarray}}\)
とすることで簡単に面積の値を導くことが出来る。

