こんにちは、リンス(@Lins016)です。
今回は三角形の面積について学習していこう。
三角形の面積の求め方
中学生のときに底辺×高さ÷2って教わったと思うけど、高さがわかっていなくても三角比を利用して高さを求めることができるからそれを利用して面積を求めていこう。
\(\small{ \begin{eqnarray}\ \mathrm{S}&=& \displaystyle \frac{1}{2}bc \sin \mathrm{A}\\
&=& \displaystyle \frac{abc}{4R}\\
&=& \displaystyle \frac{1}{2}r(a+b+c)\\
&=& \sqrt{s(s-a)(s-b)(s-c)} \ \end{eqnarray}}\)
\(\small{ \ R \ }\)は三角形の外接円の半径
\(\small{ \ r \ }\)は三角形の内接円の半径
\(\small{ \ s= \displaystyle \frac{a+b+c}{2} \ }\)
三角形の面積の求め方
図のように\(\small{ \ \mathrm{B} \ }\)から\(\small{ \ \mathrm{AC} \ }\)に垂線を下ろすと、その垂線の長さは\(\small{ \ \mathrm{AB}\sin\mathrm{A} \ }\)になるよね。だから面積の公式「底辺×高さ÷2」を計算すると、\(\small{ \ \mathrm{S}= \displaystyle \frac{1}{2}\mathrm{AC}\cdot\mathrm{AB}\sin \mathrm{A} \ }\)つまり \(\small{ \ \mathrm{S}= \displaystyle \frac{1}{2}bc\sin \mathrm{A} \ }\)になるんだ。
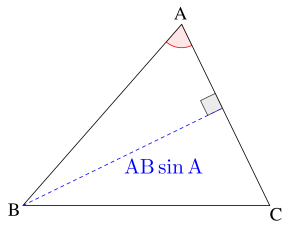
\(\small{ \ \angle \mathrm{A} \ }\)が鈍角の場合、垂線の長さは\(\small{ \ \mathrm{AB}\sin(180^{\circ}-\mathrm{A}) \ }\)になるけど、\(\small{ \ \sin(180^{\circ}-\theta)=\sin \theta \ }\)だから、鋭角のときと同じで\(\small{ \ \mathrm{AB}\sin\mathrm{A} \ }\)になるんだ。だから鈍角の場合も三角形の面積は結局\(\small{ \ \mathrm{S}= \displaystyle \frac{1}{2}bc\sin \mathrm{A} \ }\)になるからね。
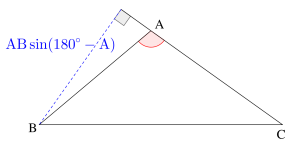
つまり2辺とその挟む角の正弦が分かっていれば面積を求めることが出来るってことがわかるよね。
ここで注意しておきたいのが、その挟む角の正弦の求め方。もちろん正弦定理を使えば、求めることが出来るけど、正弦定理が使えない場合、余弦定理から余弦を求めて、\(\small{ \ \sin^2 \theta +\cos^2 \theta=1 \ }\)から正弦を求めればいいからね。
ちなみに1辺とその両端の角がわかっている場合は
\(\small{ \ \mathrm{S}=\displaystyle\frac{a^2\sin\mathrm{B}\sin\mathrm{C}}{2\sin(\mathrm{B}+\mathrm{C})} \ }\)を使えばいい。
ちなみにこの式は正弦定理を利用して
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle \frac{1}{2}bc\sin\mathrm{A}\\[8pt]
&=&\displaystyle \frac{1}{2}\cdot\displaystyle \frac{a\sin\mathrm{B}}{\sin\mathrm{A}}\cdot\displaystyle \frac{a\sin\mathrm{C}}{\sin\mathrm{A}}\cdot\sin\mathrm{A}\\[8pt]
&=&\displaystyle \frac{1}{2}\cdot\displaystyle \frac{a^2\sin\mathrm{B}\sin\mathrm{C}}{\sin\mathrm{A}}\\[8pt]
&=&\displaystyle \frac{1}{2}\cdot\displaystyle \frac{a^2\sin\mathrm{B}\sin\mathrm{C}}{\sin\mathrm{\left\{180^{\circ}-(\mathrm{B}+\mathrm{C})\right\}}}\\[8pt]
&=&\displaystyle\frac{a^2\sin\mathrm{B}\sin\mathrm{C}}{2\sin(\mathrm{B}+\mathrm{C})} \ \end{eqnarray}}\)
って導くことができる。あまり出題されたりはしないけど、変形の仕方は知っておこう。
内接円の半径と面積
三角形のそれぞれの角の二等分線は1点で交わる。この点は内心っていって三角形の内接円の中心になるんだ。内接円は各辺に接するから内心と各頂点を結ぶと三角形が3分割されるよね。この分割した三角形のそれぞれの面積は、辺の長さ×内接円の半径×\(\small{ \ \displaystyle \frac{1}{2} \ }\)で表すことができるから、 \(\small{ \ \mathrm{S}= \displaystyle \frac{1}{2}r(a+b+c) \ }\)になるよね。
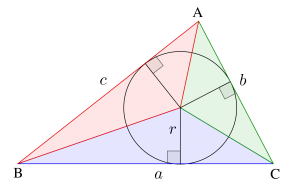
内接円の半径はこの面積の公式以外では出てこないから、内接円の半径を求める場合は面積を利用するようにしよう。
ヘロンの公式の利用
三角形の3辺がわかっている場合はヘロンの公式を利用して面積を求めよう。その方が圧倒的に早いからね。
ヘロンの公式
三角形\(\small{ \ \mathrm{ABC} \ }\)の面積を\(\small{ \ \mathrm{S} \ }\)とすると
\(\small{ \ \mathrm{S}=\sqrt{s(s-a)(s-b)(s-c)} \ }\)
ただし、\(\small{ \ s=\displaystyle \frac{a+b+c}{2} \ }\)
ただ、3辺が有理数じゃないと計算が大変だから根号を含んでる場合は、ヘロンの公式を変形した形の式を利用しよう。
ヘロンの公式の証明も確認しておこう。この面積の証明を少しイジって入試問題として出題されたりもするからね。
\(\small{ \ \triangle \mathrm{ABC} \ }\)において、\(\small{ \ a=8, \ b=5, \ c=7 \ }\)のとき次の値を求めよ。
(1)\(\small{ \ \cos \mathrm{A} \ }\)の値を求めよ。
(2)\(\small{ \ \triangle \mathrm{ABC} \ }\)の面積
(3)外接円の半径
(4)内接円の半径
(1)余弦定理より
\(\small{ \ \cos \mathrm{A}= \displaystyle \frac{5^2+7^2-8^2}{2\cdot5\cdot7}=\displaystyle \frac{1}{7} \ }\)
(2)\(\small{ \ \sin^2 \theta+\cos^2 \theta=1 \ }\)より
\(\small{ \ \sin\mathrm{A}=\sqrt{1-\left(\displaystyle \frac{1}{7}\right)^2}=\displaystyle \frac{4\sqrt{3}}{7} \ }\)
面積を\(\small{ \ \mathrm{S} \ }\)とすると
\(\small{ \ \mathrm{S}=\displaystyle \frac{1}{2}\cdot5\cdot7\cdot\displaystyle \frac{4\sqrt{3}}{7}=10\sqrt{3} \ }\)
(3)外接円の半径を\(\small{ \ \mathrm{R} \ }\)とすると正弦定理より
\(\small{ \ \displaystyle \frac{8}{\displaystyle \frac{4\sqrt{3}}{7}}=2\mathrm{R} \ }\)
\(\small{ \ \mathrm{R}=\displaystyle \frac{7\sqrt{3}}{3} \ }\)
(4)内接円の半径を\(\small{ \ r \ }\)とすると
\(\small{ \ \mathrm{S}=\displaystyle \frac{1}{2}r(a+b+c) \ }\)より
\(\small{ \ r=\displaystyle \frac{2}{8+5+7}\cdot10\sqrt{3}=\sqrt{3} \ }\)

Point
①2辺とその挟む角から面積を求める
②3辺がわかっていたらヘロンの公式を利用
\(\small{ \ \triangle \mathrm{ABC} \ }\)は\(\small{ \ 3 \ }\)辺の長さがそれぞれ\(\small{ \ a, \ b, \ 8 \ }\)で面積が\(\small{ \ 10\sqrt{3} \ }\)である。
また、\(\small{ \ a, \ b \ }\)は二次方程式\(\small{ \ x^2-12x+c=0 \ }\)の解である。このとき、\(\small{ \ \triangle \mathrm{ABC} \ }\)の外接円の半径を求めよ。
\(\small{ \ a, \ b \ }\)は二次方程式\(\small{ \ x^2-12x+c=0 \ }\)の解より、解と係数の関係から
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=12\cdots①\\
ab=c\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
面積が\(\small{ \ 10\sqrt{3} \ }\)より、\(\small{ ① \ }\)とヘロンの公式と用いると
\(\small{ \ \sqrt{10(10-a)(10-b)(10-8)}=10\sqrt{3} \ }\)
これを整理すると
\(\small{ \ ab-10a-10b+85=0 \ }\)
\(\small{ \ a+b=12 \ }\)より
\(\small{ \ ab=35 \ }\)
\(\small{ \ \therefore c=35 \ }\)
よって\(\small{ \ x^2-12x+35=0 \ }\)の解が\(\small{ \ a, \ b \ }\)より
\(\small{ \ (x-5)(x-7)=0 \ }\)
\(\small{ \ \therefore x=5,7 \ }\)
次に余弦定理を利用して
\(\small{ \ \cos\mathrm{C}=\displaystyle \frac{5^2+7^2-8^2}{2\cdot5\cdot7}=\displaystyle \frac{1}{7} \ }\)
\(\small{ \ \sin^2\mathrm{C}+\cos^2\mathrm{C}=1 \ }\)より
\(\small{ \ \sin\mathrm{C}=\sqrt{1-\cos^2\mathrm{C}}=\displaystyle \frac{4\sqrt{3}}{7} \ }\)
正弦定理より
\(\small{ \ \displaystyle \frac{8}{\displaystyle \frac{4\sqrt{3}}{7}}=2\mathrm{R} \ }\)
\(\small{ \ \therefore \mathrm{R}=\displaystyle \frac{7\sqrt{3}}{3} \ }\)

