こんにちは、リンス(@Lins016)です。
今回は格子点の個数の求め方について学習していこう。
格子点と数列
格子点とは「座標平面(空間座標)上の各成分(\(\small{ \ x \ }\)座標、\(\small{ \ y \ }\)座標、\(\small{ \ z\ }\)座標)が整数である点」のこと。
今回はある条件の中に含まれる格子点の数を求めるのに数列の和記号\(\small{ \ \displaystyle\sum \ }\)を利用する方法について勉強していこう。
条件を満たす\(\small{ \ x=k \ }\)上の格子点の個数を\(\small{ \ a_k \ }\)とするとき
ただし\(\small{ \ 0\leqq k \leqq n \ }\)で、
\(\small{ \ k \ }\)は整数とすると
\(\small{ \ \displaystyle \sum_{ k=0 }^{ n }a_k \ }\)
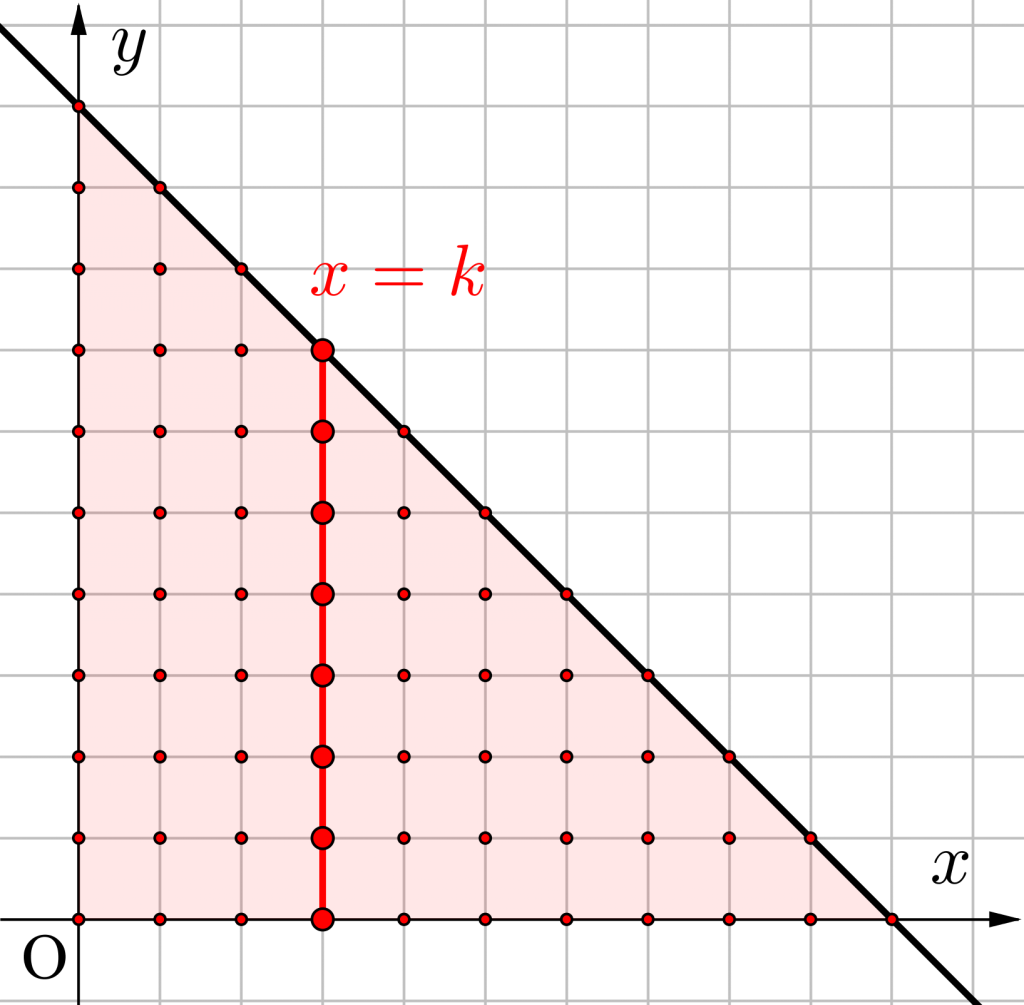
格子点の求め方の基本
格子点の求め方は、「\(\small{ \ x=k \ }\)または\(\small{ \ y=k \ }\)上の条件を満たす格子点の個数を求め、それを\(\small{ \ k=0 \ }\)(場合によっては\(\small{ \ k=0 \ }\)じゃないときもある)から足し合わせていく」ことで求めることができるんだ。
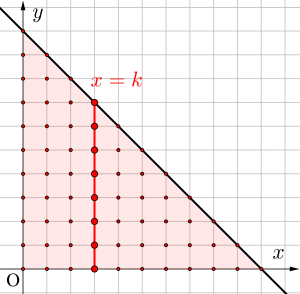
\(\small{ \ x\geqq0, \ y\geqq0, \ x+y\leqq10 \ }\)を満たす整数\(\small{ \ x, \ y \ }\)の組の総数を求めよ。
\(\small{ \ x=k \ }\)と\(\small{ \ x+y=10 \ }\)の交点の\(\small{ \ y \ }\)座標は\(\small{ \ y=10-k \ }\)
つまり\(\small{ \ x=k \ }\)上の格子点は
\(\small{ \ 10-k+1=11-k \ }\)個ある
また\(\small{ \ y\geqq0 \ }\)から\(\small{ \ k=0, \ 1, \ 2\cdots,10 \ }\)
よって求める格子点の数は
\(\small{ \ \displaystyle \sum_{ k=0 }^{ 10 }(11-k)\\
=11+ \displaystyle \sum_{ k=1 }^{ 10 }(11-k)\\
=11+110-\displaystyle\frac{1}{2}\cdot10\cdot11\\
=66 \ }\)

だってシグマの公式は\(\small{ \ k=1 \ }\)からの和になってるからね。
もちろん\(\small{ \ k=0 \ }\)から直接計算する方法もあるから計算できるなら計算してもいいけど、項数を\(\small{ \ n+1 \ }\)にしたりしないといけないから逆にミスする人もいるからね。
\(\small{ \ x=k \ }\)上の格子点の数は\(\small{ \ x \ }\)軸上の点まで含むから、\(\small{ \ x=k \ }\)と\(\small{ \ x+y=10 \ }\)の交点の\(\small{ \ y \ }\)座標に\(\small{ \ 1 \ }\)加えた数になるから注意しよう。
問題によっては\(\small{ \ x+y\lt 10 \ }\)のように直線上の点は含まない場合もあるからね。
格子点の数え方と場合分け
上の例題では\(\small{ \ x=k \ }\)上の格子点を求めて、\(\small{ \ k=0 \ }\)から\(\small{ \ k=10 \ }\)まで足したよね。
これは\(\small{ \ x=0 \ }\)上の格子点から\(\small{ \ x=10 \ }\)の格子点までを順に加えたことになる。
つまり格子点の数を縦に数えたことになるんだ。
これに対して\(\small{ \ y=k \ }\)上の格子点を求めて、それを足し合わせると格子点の数を横に数えることになるんだ。
もちろんどっちで数えても同じ数になるんだけど、問題によっては計算が複雑になる場合がある。
例えば\(\small{ \ x\geqq0, \ y\geqq0, \ x+y\leqq10 \ }\)は縦で数えても、横で数えても同じなんだけど、
\(\small{ \ x\geqq0, \ y\geqq0, \ x+2y\leqq10 \ }\)は縦で数えてるよりも横で数えたほうが簡単なんだ。
それじゃこの\(\small{ \ x\geqq0, \ y\geqq0, \ x+2y\leqq10 \ }\)を縦にも横にも数え上げて計算してみよう。
まずはさっきと同じように縦に数えてみよう。
\(\small{ \ x=k \ }\)と\(\small{ \ x+2y=10 \ }\)の交点の\(\small{ \ y \ }\)座標は\(\small{ \ k+2y=10 \ }\)から\(\small{ \ y=\displaystyle\frac{10-k}{2} \ }\)になるよね。
ってことは、この交点は\(\small{ \ k \ }\)が偶数の場合は格子点になるけど、奇数の場合は格子点にならないよね。
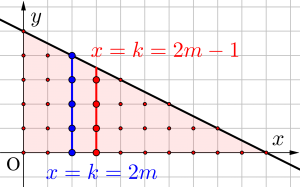
これは図を見ても確認できるよね。だから偶数と奇数の場合に分けて格子点を数え上げる必要があるんだ。
(i)\(\small{ \ k=2m \ }\)のとき
\(\small{ \ y=\displaystyle\frac{10-2m}{2}=5-m \ }\)
\(\small{ \ k\geqq0, \ y\geqq0 \ }\)より\(\small{ \ m=0, \ 1,\cdots,5 \ }\)
\(\small{ \ x=k \ }\)上の格子点の数は
\(\small{ \ 5-m+1=6-m \ }\)個
(ii)\(\small{ \ k=2m-1 \ }\)のとき
\(\small{ \ y=\displaystyle\frac{10-2m+1}{2}=\displaystyle\frac{11}{2}-m \ }\)
\(\small{ \ k\geqq0, \ y\geqq0 \ }\)より\(\small{ \ m=1, \ 2,\cdots,5 \ }\)
\(\small{ \ x=k \ }\)上の格子点の数は
\(\small{ \ 5-m+1=6-m \ }\)個
つまり求める格子点の個数は(i)(ii)より
\(\small{ \ \displaystyle \sum_{ m=0 }^{ 5 }(6-m)+\displaystyle \sum_{ m=1 }^{ 5 }(6-m)\\
=6+2\displaystyle \sum_{ m=1 }^{ 5 }(6-m)\\
=6+2\left(30-\displaystyle\frac{1}{2}\cdot5\cdot6\right)\\
=36 \ }\)
次に横に数えてみよう。
\(\small{ \ y=k \ }\)と\(\small{ \ x+2y=10 \ }\)の交点の\(\small{ \ x \ }\)座標は
\(\small{ \ x=10-2k \ }\)になるよね。
ってことは\(\small{ \ x \ }\)は常に整数になるから場合分けする必要がないんだ。
だから\(\small{ \ y=k \ }\)上の格子点の個数は\(\small{ \ 10-2k+1=11-2k \ }\)個になるんだ。
また\(\small{ \ x\geqq0, \ y\geqq0 \ }\)から\(\small{ \ k=0, \ 1,\cdots,5 \ }\)

だから求める格子点の数は
\(\small{ \ \displaystyle \sum_{ k=0 }^{ 5 }(11-2k)\\
=11+\displaystyle \sum_{ k=1 }^{ 5 }(11-2k)\\
=11+11\cdot5-2\cdot\displaystyle\frac{1}{2}\cdot5\cdot6\\
=11+55-30\\
=36 \ }\)
この問題の場合、横に数えることで場合分けが必要なかったよね。
問題によっては縦横のどっちを考えても場合分けが必要になる問題もあるけど、なるべく場合分けが少ない方を選んで計算しよう。
\(\small{ \ 3x+2y\leqq2008 \ }\)を満たす\(\small{ \ 0 \ }\)以上の整数の組\(\small{ \ (x, \ y) \ }\)の個数を求めよ。
\(\small{ \ x=k \ }\)と\(\small{ \ 3x+2y=2008 \ }\)との交点の座標は
\(\small{ \ y=1004-\displaystyle\frac{3}{2}k \ }\)
\(\small{ \ y\geqq0 \ }\)より\(\small{ \ 0\leqq k \leqq 669+\displaystyle\frac{1}{3} \ }\)
よって直線\(\small{ \ x=k \ }\)上の格子点の個数は
(i)\(\small{ \ k=2m \ (m=0, \ 1, \ ,\cdots,334) \ }\)のとき
\(\small{ \ y=1004-\displaystyle\frac{3}{2}\cdot 2m=1004-3m \ }\)
よって格子点の個数は\(\small{ \ 1005-3m \ }\)個
(ii))\(\small{ \ k=2m+1 \ (m=0, \ 1, \ ,\cdots,334) \ }\)のとき
\(\small{ \ 1004-\displaystyle\frac{3}{2}\cdot(2m+1)=1002.5-3m \ }\)
よって格子点の個数は\(\small{ \ 1003-3m \ }\)個
(i)(ii)より求める個数は
\(\small{ \ \displaystyle \sum_{ m=0 }^{ 334 }(1005-3m)+\displaystyle \sum_{ m=0 }^{ 334 }(1003-3m)\\
=\displaystyle \sum_{ m=0 }^{ 334 }\left\{(1005-3m)+(1003-3m)\right\}\\
=\displaystyle \sum_{ m=0 }^{ 334 }(2008-6m)\\
=2008+\displaystyle \sum_{ m=1 }^{ 334 }(2008-6m)\\
=2008+334\cdot2008-6\cdot\displaystyle\frac{1}{2}\cdot334\cdot335\\
=337010 \ }\)

偶奇の場合分けの場合、奇数を\(\small{ \ k=2m+1 \ }\)っておけば\(\small{ \ m=0, \ 1,\cdots,334 \ }\)になるし、\(\small{ \ k=2m-1 \ }\)っておけば\(\small{ \ m=1, \ 2,\cdots,335 \ }\)になる。
この問題の場合、偶数と奇数のそれぞれの和を\(\small{ \ m=0 \ }\)から\(\small{ \ m=334 \ }\)に合わせて計算したほうが楽だから、奇数を\(\small{ \ k=2m+1 \ }\)にしてるけど、\(\small{ \ k=2m-1 \ }\)っておいて別々に計算しても問題ないからね。
\(\small{ \ n \ }\)を自然数とする。
不等式\(\small{ \ y\leqq 2n^2, \ y=\displaystyle\frac{1}{2}x^2, \ x\geqq0 \ }\)を同時に満たす整数の組(\(\small{ \ x, \ y \ }\))の個数を求めよ。
\(\small{ \ y=2n^2 \ }\)と\(\small{ \ y=\displaystyle\frac{1}{2}x^2 \ }\)の交点の\(\small{ \ x \ }\)座標は
\(\small{ \ 2n^2=\displaystyle\frac{1}{2}x^2 \ }\)より\(\small{ \ x=2n \ }\)
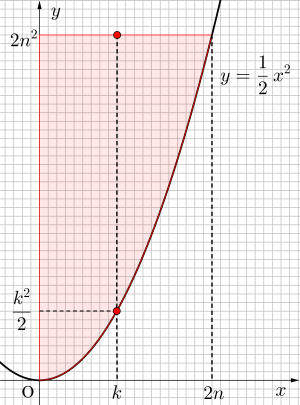
直線\(\small{ \ x=k \ (0\leqq k \leqq 2n) \ }\)上の格子点の個数は
(i)\(\small{ \ k=2m \ (0\leqq m \leqq n, \ }\)ただし\(\small{ \ m \ }\)は整数)のとき
\(\small{\begin{eqnarray} y&=&2n^2-\displaystyle\frac{1}{2}\left(2m\right)^2\\
&=&2n^2-2m^2 \ \end{eqnarray}}\)
よって格子点の個数は\(\small{ \ 2n^2-2m^2+1 \ }\)
(ii)\(\small{ \ k=2m-1 \ (1\leqq m \leqq n, \ }\)ただし\(\small{ \ m \ }\)は整数)のとき
\(\small{\begin{eqnarray} \ y&=&2n^2-\displaystyle\frac{1}{2}\left(2m-1\right)^2\\
&=&2n^2-2m^2+2m-\displaystyle\frac{1}{2} \ \end{eqnarray}}\)
よって格子点の個数は\(\small{ \ 2n^2-2m^2+2m \ }\)
(i)(ii)より求める格子点の数は
=2n^2+1+\displaystyle \sum_{ m=1 }^{ n }(2n^2-2m^2+1)+\displaystyle \sum_{ m=1 }^{ n }(2n^2-2m^2+2m)\\
=2n^2+1+2n^3-2\cdot\displaystyle\frac{1}{6}n(n+1)(2n+1)+n+2n^3-2\cdot\displaystyle\frac{1}{6}n(n+1)(2n+1)+2\cdot\displaystyle\frac{1}{2}n(n+1)\\
=\displaystyle\frac{8}{3}n^3+n^2+\displaystyle\frac{4}{3}n+1\ }\)

\(\small{ \ y=k \ }\)と\(\small{ \ y=\displaystyle\frac{1}{2}x^2 \ }\)の交点の\(\small{ \ x \ }\)座標は\(\small{ \ x=\sqrt{2k} \ }\)だから\(\small{ \ x=\sqrt{2k} \ }\)が整数になる場合とならない場合に場合分けしないといけないんだけど、これは難しいよね。
だから\(\small{ \ x=k \ }\)上の格子点を数えていくことになるんだ。
Point 格子点の個数の求め方
①\(\small{ \ x=k \ }\)または\(\small{ \ y=k \ }\)上の格子点の個数を求める
②\(\small{ \ k \ }\)の範囲に注意して格子点の和を求める

