こんにちは、リンス(@Lins016)です。
今回は空間ベクトルの点の存在範囲について学習していこう。
空間ベクトルの点の存在範囲と条件式
空間ベクトルは\(\small{ \ 3 \ }\)つの基準のベクトルで表すってことは学習したけど、今回はこの\(\small{ \ 3 \ }\)つのベクトルの係数に条件があるとき、そのベクトルの存在する位置について考えてみよう。
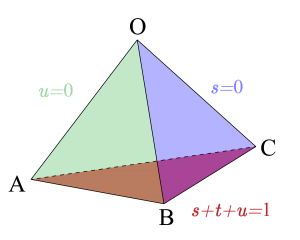
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)のとき
点\(\small{ \ \mathrm{P} \ }\)の位置は
①\(\small{ \ s+t+u=1 \ }\)のとき、平面\(\small{ \ \mathrm{ABC} \ }\)上
特に\(\small{ \ s\geqq0, \ t\geqq0, \ u\geqq0 \ }\)なら\(\small{ \ \triangle\mathrm{ABC} \ }\)内
②\(\small{ \ s=0 \ }\)のとき、平面\(\small{ \ \mathrm{OBC} \ }\)上
特に\(\small{ \ 0\leqq t \leqq1, \ 0\leqq u \leqq1 \ }\)なら\(\small{ \ \triangle\mathrm{OBC} \ }\)内
③\(\small{ \ t=0 \ }\)のとき、平面\(\small{ \ \mathrm{OAC} \ }\)上
特に\(\small{ \ 0\leqq s \leqq1, \ 0\leqq u \leqq1 \ }\)なら\(\small{ \ \triangle\mathrm{OAC} \ }\)内
④\(\small{ \ u=0 \ }\)のとき、平面\(\small{ \ \mathrm{OAB} \ }\)上
特に\(\small{ \ 0\leqq s \leqq1, \ 0\leqq t \leqq1 \ }\)なら\(\small{ \ \triangle\mathrm{OAB} \ }\)内
空間中の点Pの位置ベクトル
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)のとき
点\(\small{ \ \mathrm{P} \ }\)がどこにあるかっていうのは\(\small{ \ 3 \ }\)つのベクトルが同一平面上にない場合、\(\small{ \ s, \ t, \ u \ }\)の係数で定まるんだ。
この\(\small{ \ s, \ t, \ u \ }\)の係数で表されるベクトルは、ただの\(\small{ \ 1 \ }\)通りしかないから、係数が\(\small{ \ 1 \ }\)つでも違うと異なるベクトルってことになるからね。
条件式s+t+u=1
同一平面上のベクトルの学習で\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)のとき
点\(\small{ \ \mathrm{P} \ }\)の位置は\(\small{ \ s+t+u=1 \ }\)なら平面\(\small{ \ \mathrm{ABC} \ }\)上にあるってことを学習したよね。
忘れている人がいたら一度次の記事を読んで復習しておこう。
さらに踏み込んで考えてみると
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)は\(\small{ \ s+t+u=1 \ }\)を代入して
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+(1-s-t)\overrightarrow{\mathrm{OC}} \ }\)
これを式変形していくと
\(\small{ \ \overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OC}}=s\left(\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OC}}\right)+t\left(\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OC}}\right) \ }\)
\(\small{ \ \overrightarrow{\mathrm{CP}}=s\overrightarrow{\mathrm{CA}}+t\overrightarrow{\mathrm{CB}} \ }\)
になるよね。
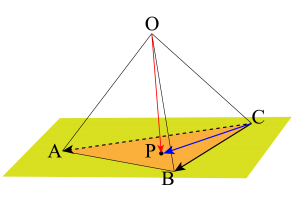
ここで点\(\small{ \ \mathrm{P} \ }\)が\(\small{ \ \triangle\mathrm{ABC} \ }\)内にある条件は
\(\small{ \ s\geqq0, \ t\geqq0, \ s+t\leqq1 \ }\)だったよね。
これは平面ベクトルの点の存在範囲で学習してるから、「?」ってなった人は復習しておこう。
\(\small{ \ s\geqq0, \ t\geqq0, \ s+t\leqq1 \ }\)は\(\small{ \ s\geqq0, \ t\geqq0, \ 1-s-t\geqq0 \ }\)
つまり\(\small{ \ s\geqq0, \ t\geqq0, \ u\geqq0 \ }\)になるんだ。
条件式s=0
次に\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)の係数のうち\(\small{ \ 1 \ }\)つが\(\small{ \ 0 \ }\)の場合について考えてみよう。
\(\small{ \ s=0 \ }\)のとき\(\small{ \ \overrightarrow{\mathrm{OP}}=t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)になるよね。
これは\(\small{ \ 2 \ }\)つのベクトルで作られる平面上に存在するベクトルになる。
だって平面ベクトルは\(\small{ \ 2 \ }\)つの基準のベクトルで表すことが出来たから、\(\small{ \ 2 \ }\)つの基準のベクトルが作る平面上に点\(\small{ \ \mathrm{P} \ }\)は存在することになるんだ。
つまり\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OC}} \ }\)の作る平面\(\small{ \ \mathrm{OBC} \ }\)上にあるってことね。
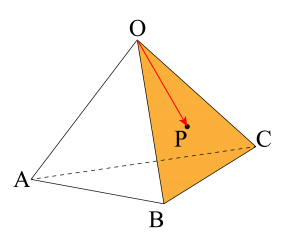
あとは平面\(\small{ \ \mathrm{OBC} \ }\)の平面ベクトルの問題として考えたらいいからね。
同じように考えると\(\small{ \ t=0 \ }\)のとき\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+u\overrightarrow{\mathrm{OC}} \ }\)になって、点\(\small{ \ \mathrm{P} \ }\)は平面\(\small{ \ \mathrm{OAC} \ }\)上に、\(\small{ \ u=0 \ }\)のとき\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)になって、点\(\small{ \ \mathrm{P} \ }\)は平面\(\small{ \ \mathrm{OAB} \ }\)上にあるって言えるよね。
「平面上にある」って条件から係数がどんな値や条件になるか考えて問題を解いていこう。
不等式と存在範囲
次に条件式が不等式の場合の存在範囲について考えてみよう。
まずは\(\small{ \ s+t+u=2, \ s\geqq0, \ t\geqq0, \ u\geqq0 \ }\)のとき\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)の点\(\small{ \ \mathrm{P} \ }\)の位置を考えてみよう。
平面ベクトルの点の存在範囲と同じように係数の和が\(\small{ \ 1 \ }\)になるように変形して
\(\small{ \ \displaystyle \frac{s}{2}+\displaystyle \frac{t}{2}+\displaystyle \frac{u}{2}=1 \ }\)
\(\small{ \ \overrightarrow{\mathrm{OP}}=\displaystyle \frac{s}{2}\cdot2\overrightarrow{\mathrm{OA}}+\displaystyle \frac{t}{2}\cdot2\overrightarrow{\mathrm{OB}}+\displaystyle \frac{u}{2}\cdot2\overrightarrow{\mathrm{OC}} \ }\)
\(\small{ \ \displaystyle \frac{s}{2}=s' \ }\)、\(\small{ \ \displaystyle \frac{t}{2}=t' \ }\)、\(\small{ \ \displaystyle \frac{u}{2}=u' \ }\)、\(\small{ \ 2\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{OA'}} \ }\)、\(\small{ \ 2\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB'}} \ }\)、\(\small{ \ 2\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{OC'}} \ }\)とすると
\(\small{ \ s'+t'+u'=1, \ s'\geqq0, \ t'\geqq0, \ u'\geqq0 \ }\)のとき\(\small{ \ \overrightarrow{\mathrm{OP}}=s'\overrightarrow{\mathrm{OA'}}+t'\overrightarrow{\mathrm{OB'}}+u'\overrightarrow{\mathrm{OC'}} \ }\)より
点\(\small{ \ \mathrm{P} \ }\)は平面\(\small{ \ \mathrm{A'B'C'} \ }\)上にあることになるよね。
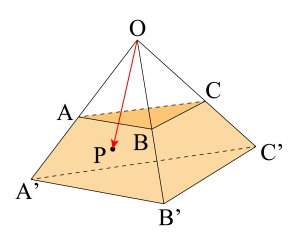
このことから\(\small{ \ 1\leqq s+t+u \leqq2, \ s\geqq0, \ t\geqq0, \ u\geqq0 \ }\)のとき\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)の点\(\small{ \ \mathrm{P} \ }\)の位置は図の色のついた位置にあるってことも言えるからね。
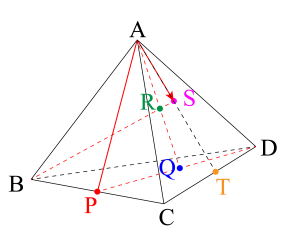
四面体\(\small{ \ \mathrm{ABCD} \ }\)の辺\(\small{ \ \mathrm{BC} \ }\)の中点を\(\small{ \ \mathrm{P} \ }\)、\(\small{ \ \mathrm{PD} \ }\)の中点を\(\small{ \ \mathrm{Q} \ }\)、\(\small{ \ \mathrm{AQ} \ }\)の中点を\(\small{ \ \mathrm{R} \ }\)とする。また、\(\small{ \ \mathrm{BR} \ }\)と平面\(\small{ \ \mathrm{ACD} \ }\)との交点を\(\small{ \ \mathrm{S} \ }\)とする。
\(\small{ \ \mathrm{AS} \ }\)を\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{AD}} \ }\)で表せ。
直線\(\small{ \ \mathrm{AS} \ }\)と\(\small{ \ \mathrm{CD} \ }\)の交点を\(\small{ \ \mathrm{T} \ }\)とするとき、\(\small{ \ \mathrm{CT:TD} \ }\)を求めよ。
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AP}}= \displaystyle\frac{1}{2 }\overrightarrow{\mathrm{AB}}+ \displaystyle\frac{1}{2 }\overrightarrow{\mathrm{AC}} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AQ}}&=&\displaystyle\frac{1}{2 }\overrightarrow{\mathrm{AP}}+ \displaystyle\frac{1}{2 }\overrightarrow{\mathrm{AD}}\\
&=&\displaystyle\frac{1}{4}\overrightarrow{\mathrm{AB}}+ \displaystyle\frac{1}{4}\overrightarrow{\mathrm{AC}}+ \displaystyle\frac{1}{2 }\overrightarrow{\mathrm{AD}} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AR}}&=&
\displaystyle\frac{1}{2 }\overrightarrow{\mathrm{AQ}}\\
&=&\displaystyle\frac{1}{8 }\overrightarrow{\mathrm{AB}}+ \displaystyle\frac{1}{8}\overrightarrow{\mathrm{AC}}+ \displaystyle\frac{1}{4 }\overrightarrow{\mathrm{AD}} \ \end{eqnarray}}\)
&=&\left(1- \displaystyle\frac{7}{8 }t\right) \overrightarrow{\mathrm{AB}}+\displaystyle\frac{1}{8 }t \overrightarrow{\mathrm{AC}}+ \displaystyle\frac{1}{4 }t \overrightarrow{\mathrm{AD}} \ \end{eqnarray}}\)
\(\small{ \ \mathrm{S} \ }\)は平面\(\small{ \ \mathrm{ACD} \ }\)上にあるので
\(\small{ \ 1- \displaystyle\frac{7}{8 }t=0 \ }\)
\(\small{ \ \therefore t= \displaystyle\frac{8}{7 } \ }\)
\(\small{ \ \overrightarrow{\mathrm{AS}}= \displaystyle\frac{1}{7 }\overrightarrow{\mathrm{AC}}+ \displaystyle\frac{2}{7} \overrightarrow{\mathrm{AD}} \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AS}}&=&\displaystyle\frac{\overrightarrow{\mathrm{AC}}+2 \overrightarrow{\mathrm{AD}}}{7}\\
&=&\displaystyle\frac{3}{7} \cdot \displaystyle\frac{ \overrightarrow{\mathrm{AC}}+2 \overrightarrow{\mathrm{AD}}}{3} \ \end{eqnarray}}\)
\(\small{ \ \overrightarrow{\mathrm{AT}}= \displaystyle\frac{ \overrightarrow{\mathrm{AC}}+2 \overrightarrow{\mathrm{AD}}}{3} \ }\)
\(\small{ \ \therefore \mathrm{CT:TD}=2:1 \ }\)

Point 空間ベクトルの点の存在範囲
①係数の条件から点の位置を考える
②特に平面上に点がある条件式は覚えておく
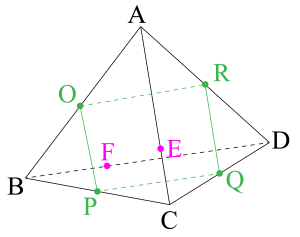
四面体\(\small{ \ \mathrm{ABCD} \ }\)において、辺\(\small{ \ \mathrm{AB, \ BC, \ CD, \ DA} \ }\)の中点をそれぞれ\(\small{ \ \mathrm{O, \ P, \ Q, \ R} \ }\)とする。このとき次の問いに答えよ。
(1)\(\small{ \ \overrightarrow{\mathrm{OQ}} \ }\)を\(\small{ \ \overrightarrow{\mathrm{OP}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OR}} \ }\)を用いて表せ。
(2)辺\(\small{ \ \mathrm{AC, \ BD} \ }\)上にそれぞれ任意の点\(\small{ \ \mathrm{E, \ F} \ }\)をとるとき、線分\(\small{ \ \mathrm{EF} \ }\)の中点は\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{O, \ P, \ Q, \ R} \ }\)を含む平面上にあることを示せ。
(1)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OQ}}&=&\overrightarrow{\mathrm{AQ}}-\overrightarrow{\mathrm{AO}}\\
&=&\displaystyle \frac{\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AD}}}{2}-\displaystyle \frac{1}{2}\overrightarrow{\mathrm{AB}}\\
&=&\displaystyle \frac{1}{2}\overrightarrow{\mathrm{AC}}+\displaystyle \frac{1}{2}\overrightarrow{\mathrm{AD}}-\displaystyle \frac{1}{2}\overrightarrow{\mathrm{AB}} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&\overrightarrow{\mathrm{AP}}-\overrightarrow{\mathrm{AO}}\\
&=&\displaystyle \frac{\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}}{2}-\displaystyle \frac{1}{2}\overrightarrow{\mathrm{AB}}\\
&=&\displaystyle \frac{1}{2}\overrightarrow{\mathrm{AC}} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OR}}&=&\overrightarrow{\mathrm{AR}}-\overrightarrow{\mathrm{AO}}\\
&=&\displaystyle \frac{1}{2}\overrightarrow{\mathrm{AD}}-\displaystyle \frac{1}{2}\overrightarrow{\mathrm{AB}} \ \end{eqnarray}}\)
\(\small{ \ \overrightarrow{\mathrm{OQ}}=\overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{OR}} \ }\)
(2)
\(\small{ \ \mathrm{E} \ }\)は辺\(\small{ \ \mathrm{AC} \ }\)上の点だから
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AE}}&=&s\overrightarrow{\mathrm{AC}} \ (0\leqq s\leqq1)\\
&=&2s\overrightarrow{\mathrm{OP}} \ \end{eqnarray}}\)
また、\(\small{ \ \mathrm{F} \ }\)は辺\(\small{ \ \mathrm{BD} \ }\)上の点だから
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{BF}}&=&t\overrightarrow{\mathrm{BD}} \ (0\leqq t\leqq1)\\
&=&2t\overrightarrow{\mathrm{OR}} \ \end{eqnarray}}\)
\(\small{ \ \mathrm{EF} \ }\)の中点を\(\small{ \ \mathrm{M} \ }\)とすると
\(\small{ \ \overrightarrow{\mathrm{OM}}\\
=\displaystyle \frac{\overrightarrow{\mathrm{OE}}+\overrightarrow{\mathrm{OF}}}{2}\\
=\displaystyle \frac{1}{2}\left\{\left(\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AE}}\right)+\left(\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{BF}}\right)\right\}\\
=\displaystyle \frac{1}{2}\left(\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{BF}}\right)\\
=\displaystyle \frac{1}{2}\left(2s\overrightarrow{\mathrm{OP}}+2t\overrightarrow{\mathrm{OR}}\right)\\
=s\overrightarrow{\mathrm{OP}}+t\overrightarrow{\mathrm{OR}} \ }\)
よって\(\small{ \ \mathrm{M} \ }\)は\(\small{ \ \mathrm{O, \ P, \ R} \ }\)で定まる平面上にある。
(1)より\(\small{ \ \mathrm{O, \ P, \ Q, \ R} \ }\)は同一平面上にあることがわかるから\(\small{ \ \mathrm{M} \ }\)は\(\small{ \ \mathrm{O, \ P, \ Q, \ R} \ }\)を含む平面にあることがわかる。


