こんにちは、リンス(@Lins016)です。
今回は二次関数のグラフの平行移動について学習していこう。
二次関数のグラフの平行移動と傾き
二次関数のグラフの平行移動は傾き、つまり\(\small{ \ x^2 \ }\)の係数が変化しないということが大前提。傾きが変化するとそれはもう平行移動じゃなくなるからね。
\(\small{ \ x \ }\)軸方向に\(\small{ \ +\alpha \ }\)
\(\small{ \ y \ }\)軸方向に\(\small{ \ +\beta \ }\)平行移動
・標準形
\(\small{ \ y=a(x-p)^2+q \ }\)を平行移動すると
\(\small{ \ y=a(x-p-\alpha)^2+q+\beta \ }\)
・一般形
\(\small{ \ y=ax^2+bx+c \ }\)を平行移動すると
\(\small{ \ y-\beta=a(x-\alpha)^2+b(x-\alpha)+c \ }\)
標準形は頂点を移動
\(\small{ \ y=a(x-p)^2+q \ }\)の標準形は頂点の座標が\(\small{ \ (p, \ q) \ }\)だから\(\small{ \ x \ }\)軸方向に\(\small{+\alpha \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{+\beta \ }\)移動させた場合、頂点の座標が\(\small{ \ (p+\alpha, \ q+\beta})\)になるよね。
傾きを変化させなかったら平行移動するから、平行移動させた関数は\(\small{ \ y=a(x-p-\alpha)^2+q+\beta \ }\)になる。つまり標準形は頂点を移動させるだけで平行移動できるんだ。
でも、この方法は二次関数特有の方法で、他の関数では利用できないから注意しよう。
一般形は\(\small{ \ x \ }\)を\(\small{ \ x-\alpha \ }\)に、\(\small{ \ y \ }\)を\(\small{ \ y-\beta \ }\)に変更
\(\small{ \ y=ax^2+bx+c \ }\)の一般形の場合は、\(\small{ \ x \ }\)を \(\small{ \ x-\alpha \ }\)に、\(\small{ \ y \ }\)を \(\small{ \ y-\beta \ }\)に書き換えることで \(\small{ \ x \ }\)軸方向に\(\small{ \ +\alpha \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ +\beta \ }\)移動させた関数の式になるんだ。
つまり平行移動した関数は、\(\small{ \ y-\beta=a(x-\alpha)^2+b(x-\alpha)+c \ }\)になる。
ちなみにこの \(\small{ \ x \ }\)を \(\small{ \ x-\alpha \ }\)に、\(\small{ \ y \ }\)を \(\small{ \ y-\beta \ }\)に書き換えて平行移動するというのは、二次関数以外の関数にも利用することが出来るからしっかりと覚えておこう。

\(\small{ \ y=x^2-2x+2 \ }\)を\(\small{ \ x \ }\)軸方向に\(\small{ \ +3 \ }\)平行移動させてみると\(\small{ \ y=x^2-2x+2 \ }\)上の点\(\small{ \ (2, \ 2) \ }\)が\(\small{ \ (5, \ 2) \ }\)に移動することになるよね。
つまり平行移動したグラフは\(\small{ \ x=5 \ }\)を代入した値が\(\small{ \ y=x^2-2x+2 \ }\)に\(\small{ \ x=2 \ }\)を代入した値と同じになればいいよね。ってことは\(\small{ \ x=5 \ }\)を代入したら\(\small{ \ x=2 \ }\)になるようにあらかじめ調整しておけばいいから、\(\small{ \ x \ }\)のところを\(\small{ \ x-3 \ }\)に書き換えることで\(\small{ \ x=5 \ }\)を代入したら\(\small{ \ x=2 \ }\)を代入したものと同じになるようにしたんだ。

\(\small{ \ y \ }\)軸方向に\(\small{+\beta \ }\)移動させる場合も同じようにすれば、\(\small{ \ y \ }\)を\(\small{ \ y-\beta \ }\)に書き換えることで平行移動させることができるよね。
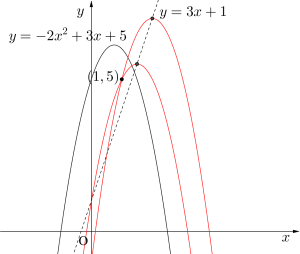
(1)放物線\(\small{ \ y=-2x^2+3x+5 \ }\)を平行移動した曲線で、頂点が直線\(\small{ \ y=3x+1 \ }\)上にあり、点\(\small{ \ (1,5) \ }\)を通る曲線の方程式を求めよ。
(2)\(\small{ \ (-3, \ 2)、(0, \ -4) \ }\)を通る放物線\(\small{ \ y=2x^2+ax+b \ }\)を\(\small{ \ x \ }\)軸方向に\(\small{ \ p \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ q \ }\)だけ移動したら\(\small{ \ y=2x^2+bx+a \ }\)になった。\(\small{ \ a,b,p,q \ }\)の値を求めなさい。
(1)傾きが\(\small{ \ -2 \ }\)、頂点を\(\small{ \ (t, \ 3t+1) \ }\)とおくと、求める放物線の方程式は\(\small{ \ y=-2(x-t)^2+3t+1 \ }\)とおける。
\(\small{ \ (1, \ 5) \ }\)を代入して、
\(\small{ \ -2(1-t)^2+3t+1=5 \ }\)
\(\small{ \ 2t^2-7t+6=0 \ }\)
\(\small{ \ (2t-3)(t-2)=0 \ }\)
\(\small{ \ t=\displaystyle \frac{3}{2}, \ 2 \ }\)
\(\small{ \ y=-2(x-2)^2+7 \ }\)
\(\small{ \ y=-2\left(x-\displaystyle \frac{3}{2}\right)^2+\displaystyle \frac{11}{2}}\)
(2)\(\small{ \ y=2x^2+ax+b \ }\)は\(\small{ \ (-3, \ 2) \ }\)、\(\small{ \ (0, \ -4) \ }\)を通るから代入して、
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
2=2\cdot(-3)^2-3a+b\\
-4=b
\end{array}
\right.
\end{eqnarray}}\)
これを解くと\(\small{ \ a=4, \ b=-4 \ }\)
\(\small{\begin{eqnarray}
y&=&2x^2+4x-4\\
&=&2(x+1)^2-6\end{eqnarray} }\)
平行移動したグラフは
\(\small{\begin{eqnarray}
y&=&2x^2-4x+4\\
&=&2(x-1)^2+2
\end{eqnarray}}\)
になるから頂点の座標を比較して、
\(\small{ \ p=2, \ q=8 \ }\)


Point 二次関数のグラフの平行移動
①平行移動は\(\small{ \ x^2 \ }\)の係数が変わらない移動のこと
②標準形は頂点の座標を移動する
③一般形は\(\small{ \ x \ }\)を\(\small{ \ x-\alpha \ }\)に、\(\small{ \ y \ }\)を\(\small{ \ y-\beta \ }\)に書き換える

