こんにちは、リンス(@Lins016)です。
今回は正弦定理について学習していこう。
正弦定理と外接円
正弦定理は\(\small{ \ \sin \ }\)(正弦)を利用した公式で三角形の辺と外接円の半径を利用した式で、角とその対辺の比が一定の値になるんだ。
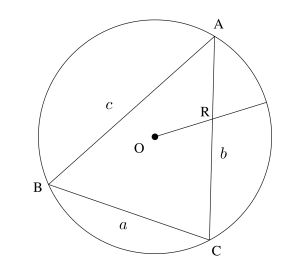
\(\normalsize{ \ \displaystyle \frac{a}{\sin\mathrm{A}}=\displaystyle \frac{b}{\sin\mathrm{B}}=\displaystyle \frac{c}{\sin\mathrm{C}}=2\mathrm{R} \ }\)
\(\small{ \ \mathrm{R} \ }\)は\(\small{ \ \triangle \mathrm{ABC} \ }\)の外接円の半径
正弦定理の証明も確認しておこう。
正弦と外接円
三角形の外接円が出てくる唯一の公式だから、外接円について問われたら正弦定理を考えよう。
また、外接円の半径を利用することで、\(\small{ \ \sin\mathrm{A}=\displaystyle \frac{a}{2R} \ }\)ってなるから、正弦を辺(長さ)だけで表すこともできるからね。
正弦と辺の長さの比
\(\small{ \ \displaystyle \frac{a}{\sin\mathrm{A}}=\displaystyle \frac{b}{\sin\mathrm{B}}=\displaystyle \frac{c}{\sin\mathrm{C}} \ }\)は、\(\small{ \ a:b:c=\sin\mathrm{A}:\sin\mathrm{B}:\sin\mathrm{C} \ }\)って書くこともできるよね。つまり正弦の比が辺の長さの比になってるんだ。
\(\small{ \ \sin\mathrm{A}:\sin\mathrm{B}:\sin\mathrm{C}=\displaystyle \frac{a}{2R}:\displaystyle \frac{b}{2R}:\displaystyle \frac{c}{2R} \ }\)とも書けるから辺の比になっているのがわかるよね。このことも頭に入れておこう。
三角形の外接円の半径が\(\small{ \ 4 \ }\)、辺 \(\small{ \ \mathrm{BC}=4 \ }\)のとき、\(\small{ \ \angle\mathrm{A} \ }\)を求めよ。
\(\small{\displaystyle \frac{\mathrm{BC}}{\sin\mathrm{A}}=2R \ }\)より
\(\small{ \ \sin\mathrm{A}=\displaystyle \frac{1}{2} \ }\)
\(\small{ \ \therefore \angle\mathrm{A}=30^{\circ}, \ 150^{\circ} \ }\)


ただし、他の辺の長さが与えられているときは他の辺の長さにも注意しよう。当然一番長い辺の対角が一番大きい角になるからね。
Point
①外接円の半径は正弦定理を利用しよう
②角とその対辺の比や外接円の半径から他の値を導こう
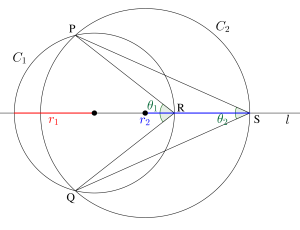
平面上で、半径\(\small{ \ r_1 \ }\)の円\(\small{ \ C_1 \ }\)と半径\(\small{ \ r_2 \ }\)の円\(\small{ \ C_2 \ }\)が異なる\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{P}}\)、\(\small{\mathrm{Q} \ }\)で交わっているとする。線分\(\small{ \ \mathrm{PQ} \ }\)の垂直二等分線を\(\small{ \ l \ }\)として、円\(\small{ \ C_1 \ }\)と\(\small{ \ l \ }\)の交点のうち円\(\small{ \ C_2 \ }\)の内部にある点を\(\small{ \ \mathrm{R} \ }\)、円\(\small{ \ C_2 \ }\)と\(\small{ \ l \ }\)の交点のうち円\(\small{ \ C_1 \ }\)の外部にある点を\(\small{ \ \mathrm{S} \ }\)とする。
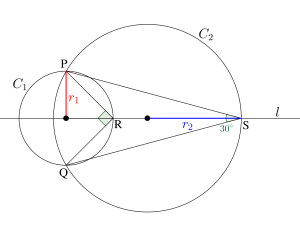
(1)\(\small{ \ \angle\mathrm{PRQ}=\displaystyle \frac{\pi}{2} \ }\)、\(\small{ \ \angle\mathrm{PSQ}=30^{\circ} \ }\)のとき、\(\small{ \ \displaystyle\frac{r_2}{r_1} \ }\)を求めよ。
(2)\(\small{ \ \angle\mathrm{PRQ}=60^{\circ} \ }\)、\(\small{ \ \angle\mathrm{PSQ}=45^{\circ} \ }\)のとき、\(\small{ \ \displaystyle\frac{r_2}{r_1} \ }\)を求めよ。
(3)\(\small{ \ \angle\mathrm{PRQ}=\theta_1 \ }\)、\(\small{ \ \angle\mathrm{PSQ}=\theta_2 \ }\)のとき、\(\small{ \ \displaystyle\frac{r_2}{r_1} \ }\)を\(\small{ \ \theta_1 \ }\)と\(\small{ \ \theta_2 \ }\)を用いて表せ。
(1)\(\small{ \ \angle\mathrm{PRQ}=90^{\circ} \ }\)より\(\small{ \ \mathrm{PQ} \ }\)は円\(\small{ \ C_1 \ }\)の直径である
\(\small{ \ \triangle \mathrm{PSQ} \ }\)で正弦定理を利用すると
\(\small{ \ \displaystyle\frac{\mathrm{PQ}}{\sin30^{\circ}}=2r_2 \ }\)
\(\small{ \ \mathrm{PQ}=2r_1 \ }\)を代入して
\(\small{ \ \therefore \displaystyle\frac{r_2}{r_1}=2 \ }\)
(2)\(\small{ \ \triangle \mathrm{PRQ} \ }\)で正弦定理を利用すると
\(\small{ \ \displaystyle\frac{\mathrm{PQ}}{\sin60^{\circ}}=2r_1 \ }\)
\(\small{ \ \therefore r_1=\displaystyle\frac{\sqrt{3}}{3}\mathrm{PQ} \ }\)
\(\small{ \ \triangle \mathrm{PSQ} \ }\)で正弦定理を利用すると
\(\small{ \ \displaystyle\frac{\mathrm{PQ}}{\sin45^{\circ}}=2r_2 \ }\)
\(\small{ \ \therefore r_2=\displaystyle\frac{\sqrt{2}}{2}\mathrm{PQ} \ }\)
\(\small{ \ \therefore \displaystyle\frac{r_2}{r_1}=\displaystyle\frac{\displaystyle\frac{\sqrt{2}}{2}\mathrm{PQ}}{\displaystyle\frac{\sqrt{3}}{3}\mathrm{PQ}}=\displaystyle\frac{\sqrt{6}}{2} \ }\)

(3)\(\small{ \ \triangle \mathrm{PRQ} \ }\)で正弦定理を利用すると
\(\small{ \ \displaystyle\frac{\mathrm{PQ}}{\sin \theta_1}=2r_1 \ }\)
\(\small{ \ \therefore r_1=\displaystyle\frac{\mathrm{PQ}}{2\sin\theta_1} \ }\)
\(\small{ \ \triangle \mathrm{PSQ} \ }\)で正弦定理を利用すると
\(\small{ \ \displaystyle\frac{\mathrm{PQ}}{\sin\theta_2}=2r_2 \ }\)
\(\small{ \ \therefore r_2=\displaystyle\frac{\mathrm{PQ}}{2\sin\theta_2} \ }\)
\(\small{ \ \therefore \displaystyle\frac{r_2}{r_1}=\displaystyle\frac{\displaystyle\frac{\mathrm{PQ}}{2\sin\theta_2}}{\displaystyle\frac{\mathrm{PQ}}{2\sin\theta_1}}=\displaystyle\frac{\sin\theta_1}{\sin\theta_2} \ }\)