こんにちは、リンス(@Lins016)です。
今回は三角関数のグラフ(1)\(\small{ \ y=\sin x \ }\)と\(\small{ \ y=\cos x \ }\)について学習していこう。
三角関数のグラフのポイント
三角関数のグラフを勉強する上で押さえるべきポイントがいくつかあるんだ。
それは波の周期、振幅、平行移動の三つ。この三つをきちんと理解していればグラフを書いたり、読み取ったりすることが簡単にできるから、今回の勉強でしっかりと押さえておこう。
ただ、\(\small{\sin \ }\)と\(\small{ \ \cos \ }\)のグラフは同じ形のグラフが平行移動したものだけど、\(\small{\tan \ }\)のグラフは、\(\small{\sin \ }\)や\(\small{ \ \cos \ }\)のグラフとは全く異なるグラフだから\(\small{\tan \ }\)のグラフは次の機会に学習していくからね。
\(\small{ \ y=\sin x \ }\)・\(\small{ \ y=\cos x \ }\)のグラフ

最終形を覚えておこう
今回学習するのは\(\small{y=\mathrm{A}\sin n(x-\alpha)+\beta}\)のグラフ。もちろん\(\small{ \ \sin \ }\)じゃなくても\(\small{ \ \cos \ }\)の\(\small{y=A\cos n(x-\alpha)+\beta}\)グラフでも考え方は同じだからね。
\(\small{ \ A, \ n, \ \alpha, \ \beta \ }\)の値によってグラフがどのように変化するのか考えていこう。
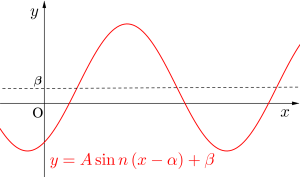
グラフ(波)の周期を理解しよう
三角関数のグラフでは\(\small{ \ x \ }\)の係数でグラフの\(\small{ \ x \ }\)軸方向の幅(波の周期)が決定するんだ。
図でも確認できるけど、\(\small{ \ n \ }\)が大きい値だと波の周期は短くなり、\(\small{ \ n \ }\)が小さい値だと波の周期は長くなってるよね。
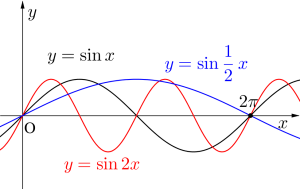
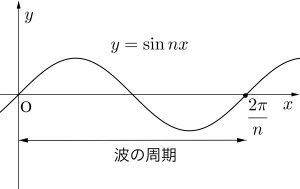
\(\small{ \ y=\sin nx \ }\)の波の周期は\(\small{ \ \displaystyle \frac{2\pi}{n} \ }\)になる。
三角関数のグラフは平行移動したりしていても波の周期は変化しないから、\(\small{ \ x \ }\)の係数で周期が決まることを覚えておこう。
グラフを答えに書く問題っていうのは定期試験ぐらいにしか出題されないけど、グラフから読み取る問題や、グラフを利用して解く問題っていうのは入試でも出題されるから、グラフは正確にかけるようになっておきたいよね。その一歩目がこの波の周期になるからね。
振幅を理解しよう
次に振幅について学習していこう。
三角関数のグラフは\(\small{ \ x \ }\)の係数の\(\small{ \ n \ }\)の値によって\(\small{ \ x \ }\)軸方向に拡大縮小したけど、振幅は\(\small{ \ \mathrm{A} \ }\)の値によって\(\small{ \ y \ }\)軸方向に拡大縮小する。
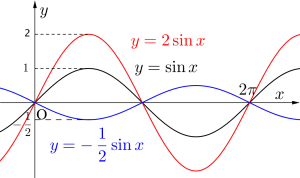
\(\small{ \ \mathrm{A} \ }\)が負のとき、グラフが\(\small{ \ x \ }\)軸に対して反転するから注意しておこう。
グラフの平行移動を理解しよう
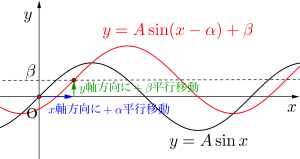
グラフの平行移動は、二次関数の平行移動で学習したように、\(\small{ \ x \ }\)を\(\small{ \ x-\alpha \ }\)に、\(\small{ \ y \ }\)を\(\small{ \ y-\beta \ }\)に書き換えることで\(\small{ \ x \ }\)軸方向に\(\small{ \ +\alpha \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ +\beta \ }\)平行移動したよね。
もちろん三角関数のグラフも同じ手順で平行移動することが出来るんだ。
つまり\(\small{ \ y= \mathrm{A}\sin x \ }\)のグラフを\(\small{ \ x \ }\)軸方向に\(\small{ \ +\alpha \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ +\beta \ }\)平行移動したグラフは\(\small{ \ y-\beta= \mathrm{A}\sin(x-\alpha) \ }\)になるんだ。
ただ、注意しておきたいのが、\(\small{ \ y=\sin\left(2x- \displaystyle \frac{\pi}{3}\right) \ }\)のグラフ。
これは\(\small{ \ y=\sin2x \ }\)のグラフを\(\small{ \ x \ }\)軸方向に \(\small{ \ \displaystyle \frac{\pi}{3} \ }\)平行移動したグラフって言いたくなるけど違うんだ。
\(\small{ \ y=\sin2\left(x- \displaystyle \frac{\pi}{6}\right) \ }\)って変形して、\(\small{ \ y=\sin2x \ }\)のグラフを\(\small{ \ x \ }\)軸方向に\(\small{ \ \displaystyle \frac{\pi}{6} \ }\)平行移動したグラフってことになるからね。
三角関数グラフの書き方まとめ
\(\small{y=\mathrm{A}\sin n(x-\alpha)+\beta}\)のとき、
・\(\small{ \ n \ }\)は\(\small{ \ x \ }\)軸に沿った拡大縮小、
・\(\small{ \ \mathrm{A} \ }\)は\(\small{ \ y \ }\)軸に沿った拡大縮小、
・\(\small{ \ \alpha、\beta \ }\)は平行移動
になるからね。

今回は\(\small{ \ \sin \ }\)のグラフで考えたけど、\(\small{ \ \cos \ }\)のグラフの場合も全く同じで、\(\small{y=\mathrm{A}\cos n(x-\alpha)+\beta}\)のとき、\(\small{ \ n \ }\)は\(\small{ \ x \ }\)軸に沿った拡大縮小、\(\small{ \ \mathrm{A} \ }\)は\(\small{ \ y \ }\)軸に沿った拡大縮小、\(\small{ \ \alpha、\beta \ }\)は平行移動になるから覚えておこう。
下図のグラフの\(\small{ \ \mathrm{A}, \ \mathrm{B}, \ a, \ b \ }\)の値を求めよ。
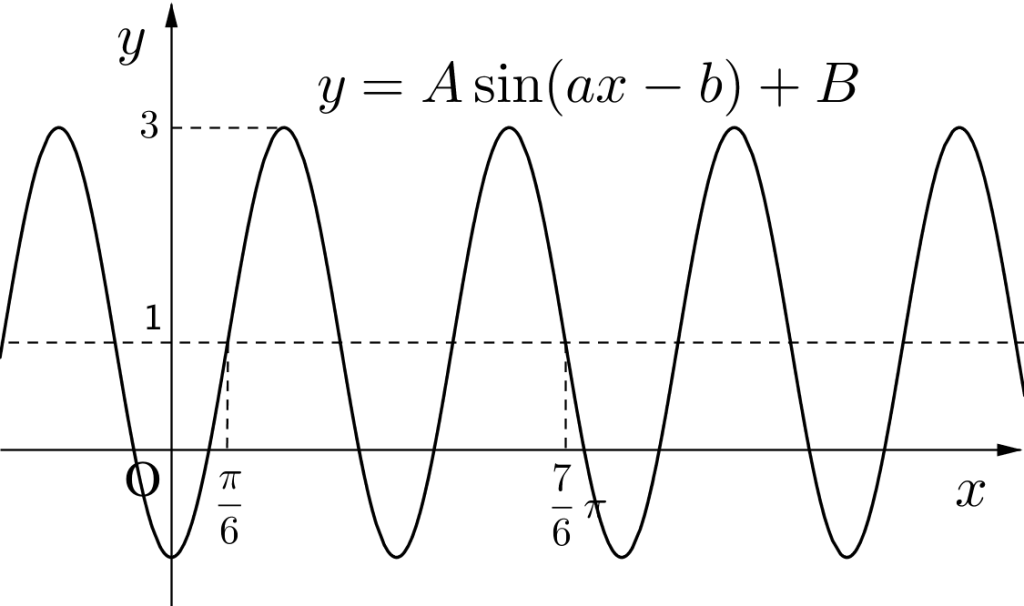
\(\small{ \ x \ }\)の係数が\(\small{ \ a \ }\)より、波の周期から
\(\small{ \ \displaystyle \frac{2\pi}{a}\cdot\displaystyle \frac{3}{2}=\displaystyle \frac{7}{6}\pi-\displaystyle \frac{\pi}{6} \ }\)
\(\small{ \ \therefore a=3 \ }\)
\(\small{ \ y=\mathrm{A}\sin3\left(x-\displaystyle \frac{b}{3}\right)+B \ }\)と変形すると、\(\small{ \ y=\mathrm{A}\sin3x+B \ }\)のグラフを\(\small{ \ x \ }\)軸方向に\(\small{ \ \displaystyle \frac{b}{3} \ }\)移動したグラフになる。
よって図のグラフより\(\small{ \ \displaystyle \frac{b}{3}=\displaystyle \frac{\pi}{6} \ }\)\(\small{ \ \therefore b=\displaystyle \frac{\pi}{2} \ }\)
また、図のグラフより\(\small{ \ y \ }\)軸方向に\(\small{ \ +1 \ }\)移動しているので\(\small{ \ \mathrm{B}=1 \ }\)
振幅から\(\small{ \ \mathrm{A}=3-1=2\ }\)

Point 三角関数のグラフ(1)
①グラフの式から波の周期・振幅・平行移動を見つけよう。
②\(\small{ \ x \ }\)の係数でくくって、平行移動を考えよう。
\(\small{ \ \sin\left(2x- \displaystyle \frac{\pi}{4}\right) = \displaystyle \frac{4}{5} (0\leqq x \leqq 2\pi) }\) を満たす角を小さい方から\(\small{ \ \alpha、\beta、\gamma、\omega \ }\)とするとき、 \(\small{ \ \alpha+\omega \ }\)の値を求めよ。
\(\small{ \ y=\sin\left(2x-\displaystyle \frac{\pi}{4}\right) \ }\)と\(\small{ \ y=\displaystyle \frac{4}{5} \ }\)のグラフの交点を考える。
\(\small{ \ y=\sin\left(2x-\displaystyle \frac{\pi}{4}\right)=\sin2\left(x-\displaystyle \frac{\pi}{8}\right) \ }\)より波の長さが\(\small{ \ \pi \ }\)の\(\small{ \ y=\sin 2x \ }\)のグラフを\(\small{ \ x \ }\)軸方向に\(\small{ \ \displaystyle \frac{\pi}{8} \ }\)平行移動したグラフになる。
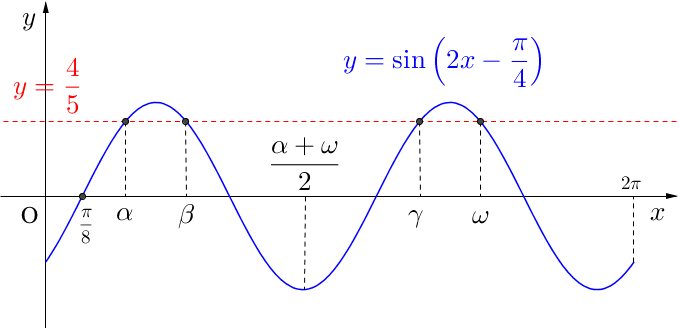
ここで\(\small{ \ \alpha \ }\)と\(\small{ \ \omega \ }\)の中点はグラフが対称になっているので、図のようにちょうどグラフの谷の部分になる。
よって\(\small{ \ \displaystyle \frac{\alpha+\omega}{2} =\displaystyle \frac{\pi}{8}+\displaystyle \frac{3}{4}\pi\ }\)
\(\small{ \ \therefore \alpha+\omega= \displaystyle \frac{7}{4}\pi \ }\)


