こんにちは、リンス(@Lins016)です。
今回は点と座標について学習していこう。
点に関する覚えるべき式
点ってきくと”ただの座標でしょ?”って思いがちだけど、意外に覚えないといけない式も多い。普段よく使っているものから、めったに使わない式まで、きちんと整理しておこう。
\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A}(x_1、y_1) \ }\)と\(\small{ \ \mathrm{B}(x_2、y_2) \ }\)、\(\small{ \ \mathrm{C}(x_3、y_3) \ }\)のとき
・\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{AB} \ }\)間の距離
\(\small{ \ \quad \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \ }\)
・\(\small{ \ \mathrm{AB} \ }\)を\(\small{ \ m:n \ }\)に内分する点
\(\small{ \ \quad \left(\displaystyle \frac{nx_1+mx_2}{m+n}、\displaystyle \frac{ny_1+my_2}{m+n}\right) \ }\)
・\(\small{ \ \mathrm{AB} \ }\)を\(\small{ \ m:n \ }\)に外分する点
\(\small{ \ \quad \left(\displaystyle \frac{-nx_1+mx_2}{m-n}、\displaystyle \frac{-ny_1+my_2}{m-n}\right) \ }\)
・三角形\(\small{ \ \mathrm{ABC} \ }\)の重心
\(\small{ \ \quad \left(\displaystyle \frac{x_1+x_2+x_3}{3}、\displaystyle \frac{y_1+y_2+y_3}{3}\right) \ }\)
今回は図形と方程式の単元で学習してるけど、座標はベクトルの成分表示にもなるから、内分点や外分点、重心ともにベクトルでも利用するから覚えておこう。
点の置き方を工夫しよう
座標を求めるためには、その点の\(\small{ \ x \ }\)座標、\(\small{ \ y \ }\)座標を文字でおいて方程式を解くというのが普通のやり方になる。
ただし、\(\small{ \ x \ }\)軸上の点を\(\small{ \ (x、0) \ }\)としたり、条件がある場合は、なるべく文字をなるべく少なくおくようにしよう。
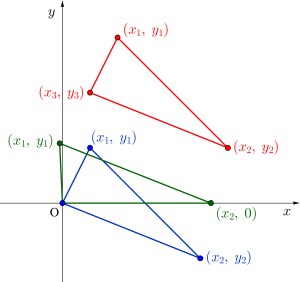
例えばある任意の三角形について考える場合、3点を\(\small{ \ (x_1、y_1)、(x_2、y_2)、(x_3、y_3) \ }\)とすると文字を6個使うことになるけど、このうち一つを原点すれば、\(\small{ \ (0、0)、(x_1、y_1)、(x_2、y_2) \ }\)となり文字が4個でいいよね。さらに工夫すると一つを原点、もう一つを\(\small{ \ x \ }\)軸上にすると、\(\small{ \ (0、0)、(x_1、y_1)、(x_2、0) \ }\)になるから文字が3個でいいよね。このように点の置き方を工夫することで計算量がかなり変わるからなるべく少ない計算量ですむように工夫しよう。
次の点の座標を求めよ。
(1)点\(\small{ \ (3、4) \ }\)に関して\(\small{ \ (-1、8) \ }\)と対称な点の座標
(2)\(\small{ \ (1、-3)、(3、2) \ }\)から等距離にある\(\small{ \ y=2x \ }\)上の点の座標
(1)対称な点\(\small{ \ (x、y) \ }\)と\(\small{ \ (-1、8) \ }\)の中点が\(\small{ \ (3、4) \ }\)になるので、
\(\small{ \ \displaystyle \frac{x-1}{2}=3 \quad \therefore x=7}\)
\(\small{ \ \displaystyle \frac{y+8}{2}= 4 \quad \therefore y=0 }\)
よって求める点の座標は\(\small{ \ (x、y)=(7、0) \ }\)
(2)\(\small{ \ y=2x \ }\)上の点を\(\small{ \ (t、2t) \ }\)とすると
これを解いて\(\small{ \ t=\displaystyle \frac{1}{8} \ }\)
よって求める点の座標は\(\small{ \ (x、y)=\left(\displaystyle \frac{1}{8}、\displaystyle \frac{1}{4}\right) \ }\)

Point
①点の座標を求めるときは、未知数をおいて、題意から方程式を作ろう。
②未知数が2つの場合は式を2つ、1つの場合は式を1つ作ろう
③直線上の点は\(\small{ \ x \ }\)座標、\(\small{ \ y \ }\)座標を一つの文字で表そう
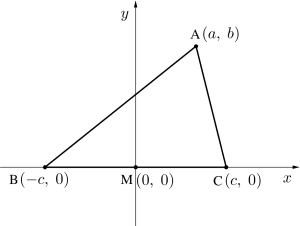
三角形\(\small{ \ \mathrm{ABC} \ }\)の辺\(\small{ \ \mathrm{BC} \ }\)の中点を\(\small{ \ \mathrm{M} \ }\)とするとき\(\small{ \ \mathrm{AB}^2+\mathrm{AC}^2=2\left(\mathrm{AM}^2+\mathrm{BM}^2\right) \ }\)が成り立つことを示せ。
\(\small{ \ \mathrm{M、A、B、C} \ }\)の座標を\(\small{ \ (0、0)、(a、b)、(-c、0)、(c、0) \ }\)とすると
左辺\(\small{=(a+c)^2+b^2+(c-a)^2+b^2\ }\)
\(\small{\hspace{ 17pt }=2(a^2+b^2+c^2)}\)
右辺\(\small{=2(a^2+b^2+c^2) \ }\)
よって左辺=右辺