こんにちは、リンス(@Lins016)です。
今回は\(\small{ \ 2 \ }\)つの直線の交点を通る直線の方程式について学習していこう。
直線の決定条件
直線はある\(\small{ \ 2 \ }\)点を結ぶことによって作成される図形だよね。つまり直線の方程式を求めるためには、直線上の\(\small{ \ 2 \ }\)点が与えられていると求めることができるってことになる。
今回学習するのは\(\small{ \ 2 \ }\)つの直線の交点とその点以外のもう\(\small{ \ 1 \ }\)点を通る直線の方程式の求め方なんだけど、\(\small{ \ 2 \ }\)つの直線の交点を求めてもいいけど、交点を求めずに\(\small{ \ 1 \ }\)つの式を\(\small{ \ k \ }\)倍して加えて方程式を導こう。
\(\small{ax+by+c=0 \ }\)と\(\small{ \ px+qy+r=0 \ }\)の交点を通る直線
\(\small{ax+by+c+k(px+qy+r)=0}\)
\(\small{ax+by+c=0 \ }\)と\(\small{ \ px+qy+r=0 \ }\)の交点を通る直線は、一つの式を\(\small{ \ k \ }\)倍して加えよう。
片方の式を\(\small{ \ k \ }\)倍して加える
\(\small{ \ 2 \ }\)つの直線のうち、どちらかの式を\(\small{ \ k \ }\)倍して加えよう。ただし、\(\small{ \ y=mx+n \ }\)の形じゃなく\(\small{ \ ax+by+c=0 \ }\)の形に変形して\(\small{ \ k \ }\)倍して加えるようにしよう。加えた式が\(\small{ \ 2 \ }\)つの直線の交点を通る直線になるんだ。
加えた方程式\(\small{ \ ax+by+c+k(px+qy+r)=0 \ }\)は\(\small{ \ x、y \ }\)ともに一次式だから直線の方程式って言える。
しかも\(\small{ \ 2 \ }\)つの直線の交点は\(\small{ \ ax+by+c=0 \ }\)も\(\small{ \ px+qy+r=0 \ }\)も満たす。
だから\(\small{ \ ax+by+c+k(px+qy+r)=0 \ }\)も満たすよね。
つまり\(\small{ \ ax+by+c+k(px+qy+r)=0 \ }\)は\(\small{ \ 2 \ }\)つの直線の交点を通る直線って言えるんだ。
\(\small{ \ y=2x+1 \ }\)と\(\small{ \ y=-3x+4 \ }\)の交点と\(\small{ \ (3,3) \ }\)を通る直線の方程式を求めよ。
\(\small{ \ y=2x+1 \ }\)と\(\small{ \ y=-3x+4 \ }\)の交点を通る直線の方程式は、
\(\small{ \ 2x-y+1+k(3x+y-4)=0 \ }\)とおける。
これが\(\small{ \ (3,3) \ }\)を通るので、代入すると
\(\small{2\cdot3-3+1+k(3\cdot3+3-4)}\)=0
\(\small{4-8k=0}\)
\(\small{\therefore \quad k=-\displaystyle \frac{1}{2}}\)
これを式に代入して\(\small{ \ 2x-y+1-\displaystyle \frac{1}{2}(3x+y-4)=0}\)
整理して\(\small{ \ x-3y+6=0 \ }\)となる。

Point 2つの直線の交点を通る直線の方程式
①\(\small{ \ 2 \ }\)つの直線の交点を通る直線は片方の式を\(\small{ \ k \ }\)倍して加えよう
②\(\small{ \ k \ }\)を定める場合は他の\(\small{ \ 1 \ }\)点を代入して定めよう
直線\(\small{ \ l:(x-2y+3)+k(x-y-1)=0 \ }\)と点\(\small{ \ \mathrm{P}(1、3)、\mathrm{Q}(5、1) \ }\)がある。
以下の問いに答えよ。
(1)\(\small{ \ k \ }\)にどのような値を与えても直線\(\small{ \ l \ }\)が通る定点を求めよ。
(2)線分\(\small{ \ \mathrm{PQ} \ }\)と直線\(\small{ \ l \ }\)が交わるような\(\small{ \ k \ }\)の値の範囲を求めよ。
(3)線分\(\small{ \ \mathrm{PQ} \ }\)の点で\(\small{ \ l \ }\)と交点となりえない点の座標を求めよ。
(1)任意の\(\small{ \ k \ }\)の値に対して\(\small{ \ x-2y+3+k(x-y-1)=0 \ }\)を満たす\(\small{ \ (x、y) \ }\)は\(\small{ \ x-2y+3+k(x-y-1)=0 \ }\)を\(\small{ \ k \ }\)についての恒等式と考えると
\(\small{ \ x-2y+3=0 \ }\)かつ\(\small{ \ x-y-1=0 \ }\)
これを解いて\(\small{ \ (x、y)=(5、4) \ }\)

(2)(i)\(\small{ \ k\neq -2 \ }\)のとき直線\(\small{ \ l \ }\)は\(\small{ \ (5、4) \ }\)を通り、傾き\(\small{ \ \displaystyle \frac{1+k}{2+k} \ }\)の直線だから線分\(\small{ \ \mathrm{PQ} \ }\) と交わる範囲は図より
傾き\(\small{ \ \displaystyle \frac{1+k}{2+k} \ }\)が\(\small{ \ \displaystyle \frac{1}{4} \ }\)以上であればよい。
\(\small{ \displaystyle \frac{1+k}{2+k} \geqq \displaystyle \frac{1}{4} \ }\)
(a)\(\small{ \ k\gt -2 \ }\)
\(\small{ \ 4(1+k)\geqq 2+k \ }\)
これを解いて\(\small{ \ k \geqq -\displaystyle \frac{2}{3} \ }\)
\(\small{ \ k\gt -2 \ }\)より\(\small{ \ k \geqq -\displaystyle \frac{2}{3} \ }\)
(b)\(\small{ \ k\lt -2 \ }\)
\(\small{ \ 4(1+k)\leqq 2+k \ }\)
これを解いて\(\small{ \ k \leqq -\displaystyle \frac{2}{3} \ }\)
\(\small{ \ k\lt -2 \ }\)より\(\small{ \ k \lt -2 \ }\)
(ii)\(\small{ \ k=-2 \ }\)のとき直線\(\small{ \ l \ }\)は\(\small{ \ x=5 \ }\)となり、線分\(\small{ \ \mathrm{PQ} \ }\)を通る
(i)(ii)より\(\small{ \ k \leqq -2、k\geqq -\displaystyle \frac{2}{3} \ }\)
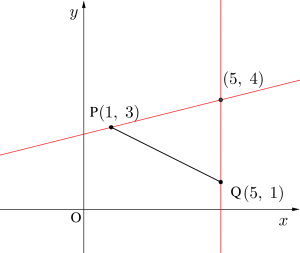
(3)直線\(\small{ \ l \ }\)の式は\(\small{ \ x-y-1=0 \ }\)かつ\(\small{ \ x-2y-3\neq0 \ }\)を満たす\(\small{ \ k \ }\)は存在しないから\(\small{ \ l \ }\)は直線\(\small{ \ x-y-1=0 \ }\)上にあって直線\(\small{ \ x-2y+3=0 \ }\)上にない点は通らない。よって線分\(\small{ \ \mathrm{PQ} \ }\)の方程式が\(\small{ \ x+2y-7=0(1\leqq x \leqq 5) \ }\)から線分\(\small{ \ \mathrm{PQ} \ }\)は直線\(\small{ \ x-y-1=0 \ }\) と点\(\small{ \ (3、2) \ }\)で交わるので、点\(\small{ \ (3、2) \ }\)は直線\(\small{ \ x-2y+3=0 \ }\)にはないから、求める点は\(\small{ \ (3、2) \ }\)


\(\small{\overbrace{ (x-2y+3)}^{ ① }+ k\overbrace{(x-y-1)}^{ ② }=0 \ }\)とすると
\(\small{①}\)と\(\small{②}\)上にない点\(\small{ \ \mathrm{A} \ }\)、\(\small{①}\)上の点\(\small{ \ \mathrm{B} \ }\)、\(\small{②}\)上の点\(\small{ \ \mathrm{C} \ }\)のいずれかと、\(\small{ \ x-2y-3=0 \ }\)と\(\small{ \ x-y-1=0 \ }\)の交点を通る直線について考えてみよう。
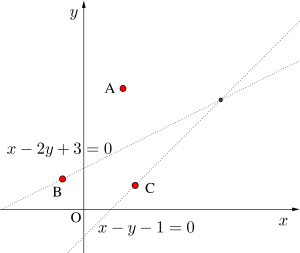
\(\small{ \ \mathrm{A} \ }\)の座標を式に代入すると、\(\small{①②}\)ともに\(\small{ \ 0 \ }\)にならないから与式が成り立つ\(\small{ \ k \ }\)が\(\small{ \ 1 \ }\)つ存在する。つまりその\(\small{ \ k \ }\)を式に代入すると\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ x-2y-3=0 \ }\)と\(\small{ \ x-y-1=0 \ }\)の交点を通る直線が求まる。
次に\(\small{ \ \mathrm{B} \ }\)の座標を式に代入すると、\(\small{①}\)は\(\small{ \ 0 \ }\)、\(\small{②}\)は\(\small{ \ 0 \ }\)にならないから\(\small{ \ k=0 \ }\)で与式は成り立つ。つまり\(\small{ \ \mathrm{B} \ }\)と\(\small{ \ x-2y-3=0 \ }\)と\(\small{ \ x-y-1=0 \ }\)の交点を通る直線は\(\small{ \ k=0 \ }\)のときで\(\small{ \ x-2y-3=0 \ }\)になる。
最後に\(\small{ \ \mathrm{C} \ }\)の座標を式に代入すると、\(\small{②}\)は\(\small{ \ 0 \ }\)、\(\small{①}\)は\(\small{ \ 0 \ }\)にならないから与式を成立させる\(\small{ \ k \ }\)は存在しない。つまり\(\small{ \ x-y-1=0 \ }\)だけはどんな\(\small{ \ k \ }\)の値を代入しても表すことができないんだ。

