こんにちは、リンス(@Lins016)です。
今回は三次関数のグラフと極大・極小について学習していこう。
三次関数のグラフ
三次関数のグラフを書く場合、まずは接線の傾き、つまり\(\small{ \ f'(x) \ }\)がどう変化するかを考えて増減表を書いてからグラフを書こう。
なんで接線の傾きの変化を考えるかというと、接線の傾きが正の場合、関数は増加することになるし、接線の傾きが負の場合、グラフは減少することになるから、接線の傾きの正負を考えることで、グラフがどんな形をしているか考えることができるんだ。
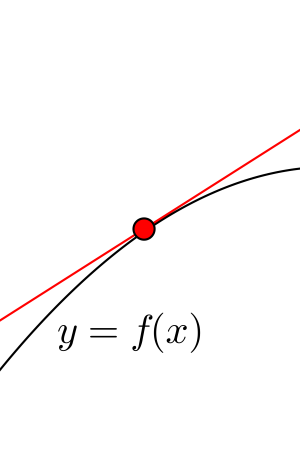
①接線の傾きが正の場合
下図のように接線が\(\small{ \ y=f(x) \ }\)より上側にある場合と下側にある場合の2パターンある。どちらも\(\small{ \ x \ }\)が増加すると\(\small{ \ y \ }\)も増加していることが確認できる。つまり接線の傾きが正の場合、関数は増加することが確認できる。

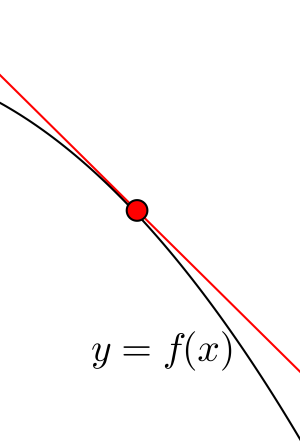
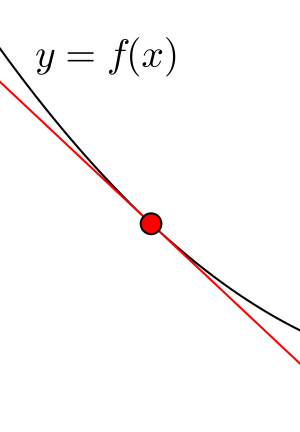
②接線の傾きが負の場合
下図のように接線が\(\small{ \ y=f(x) \ }\)より上側にある場合と下側にある場合の2パターンある。どちらも\(\small{ \ x \ }\)が増加すると\(\small{ \ y \ }\)も減少していることが確認できる。つまり接線の傾きが負の場合、関数は減少することが確認できる。
極大値・極小値とは
二次関数の場合は、平方完成して頂点を求めることでグラフを書くことが出来たよね。三次関数の場合も極値とよばれる点を求めることでグラフを書くことができる。
極値とは接線の傾きが\(\small{ \ 0 \ }\)となり、かつその前後で接線の傾きの符号が変化する点の\(\small{ \ y \ }\)座標の値のことで、特に接線の傾きが正から負に変化する点を極大値、負から正に変化する点を極小値っていうからね。
極値を求めるには\(\small{ \ f'(x)=0 \ }\)から接線の傾きが\(\small{ \ 0 \ }\)になる\(\small{ \ x \ }\)を求めて、\(\small{ \ y \ }\)座標の値を調べよう。
増減表とは
極値を求めたら、グラフを書く前に増減表を書こう。
増減表とは、\(\small{ \ x \ }\)の変化によって\(\small{ \ y \ }\)がどのように変化しているかを表にしたもので、
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 3 & \cdots \\
\hline
y’& + & 0 & - & 0 & + \\
\hline
y & \nearrow & 5 & \searrow & -27 & \nearrow
\end{array} \ }\)
のような表のこと。
これを書くことによって簡単にグラフを書くことができるんだ。
よく増減表を省略する人がいるけど、増減表を省略したら、その代わりに「\(\small{ \ x\lt-1, \ x\gt3 \ }\)で\(\small{ \ f(x) \ }\)は増加、\(\small{ \ -1\leqq x \leqq 3 \ }\)で\(\small{ \ f(x) \ }\)は減少」ってことを書かないといけないから、増減表を書いたほうが絶対楽だから、増減表を書くようにしよう。
三次関数のグラフの書き方
三次関数のグラフを書く手順は常に一緒だから、その方法をきちんとマスターして、常に正確にグラフをかけるようにしよう。
①\(\small{ \ y=f(x) \ }\)を微分して、\(\small{ \ f'(x) \ }\)を求めよう。
②\(\small{ \ f'(x)=0 \ }\)を満たす\(\small{ \ x \ }\)の値を求めよう。
③増減表の枠を作成しよう。
ただし、②で求めた\(\small{ \ x \ }\)の値の個数に注意して枠を作成すること。
④\(\small{ \ f'(x) \ }\)の欄に\(\small{ \ +, \ 0, \ - \ }\)を書き込もう。
このとき\(\small{ \ f'(x) \ }\)が2次関数になるから、\(\small{ \ x^2 \ }\)の係数の符号に注意して\(\small{ \ +, \ 0, \ - \ }\)を書き込むこと。
⑤\(\small{ \ f(x) \ }\)の欄に\(\small{ \ \nearrow, \ \searrow \ }\)を書き込もう。
ただし、\(\small{ \ f'(x) \ }\)の欄が\(\small{ \ + \ }\)の場合関数が増加するから\(\small{ \ \nearrow \ }\)を、\(\small{ \ - \ }\)の場合関数が減少するから\(\small{ \ \searrow \ }\)を書き込むこと。
⑥最後に②で求めた\(\small{ \ x \ }\)の値を代入した\(\small{ \ y \ }\)座標を求めよう。
ただし、②で\(\small{ \ f'(x)=0 \ }\)を満たす\(\small{ \ x \ }\)の値が存在しない場合や、解が1つしかなかった場合は極値を持たないので単調増加や単調減少のグラフになる。
次のグラフを書け。
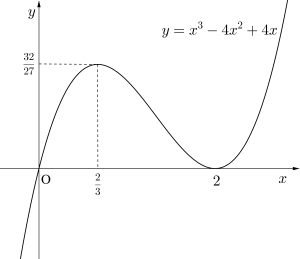
(1)\(\small{ \ y=x^3-4x^2+4x \ }\)
(2)\(\small{ \ y=-x^3+3x \ }\)
(3)\(\small{ \ y=x^3-3x^2+3x \ }\)
(1)\(\small{ \ y=x^3-4x^2+4x \ }\)
\(\small{ \ y'=3x^2-8x+4 \ }\)
\(\small{ \ y'=0 \ }\)とすると
\(\small{ \ 3x^2-8x+4=0 \ }\)
\(\small{ \ (3x-2)(x-2)=0 \ }\)
\(\small{ \ x=2, \displaystyle \frac{2}{3} \ }\)
増減表を書くと
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & \displaystyle \frac{2}{3} & \cdots & 2 & \cdots \\
\hline
y’& + & 0 & - & 0 & + \\
\hline
y & \nearrow & \displaystyle \frac{32}{27} & \searrow & 0 & \nearrow
\end{array} \ }\)
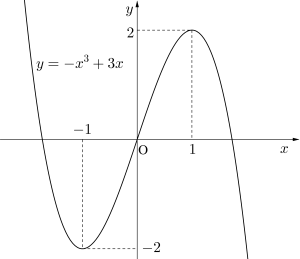
(2)\(\small{ \ y=-x^3+3x \ }\)
\(\small{ \ y'=-3x^2+3 \ }\)
\(\small{ \ y'=0 \ }\)とすると
\(\small{ \ -3x^2+3=0 \ }\)
\(\small{ \ (x+1)(x-1)=0 \ }\)
\(\small{ \ x=-1, 1 \ }\)
増減表を書くと
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 1 & \cdots \\
\hline
y’& - & 0 & + & 0 & - \\
\hline
y & \searrow & -2 & \nearrow & 2 & \searrow
\end{array} \ }\)
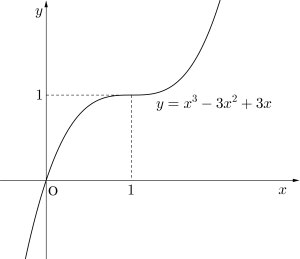
(3)\(\small{ \ y=x^3-3x^2+3x \ }\)
\(\small{ \ y'=3x^2-6x+3 \ }\)
\(\small{ \ y'=0 \ }\)とすると
\(\small{ \ 3x^2-6x+2=0 \ }\)
\(\small{ \ (x-1)^2=0 \ }\)
\(\small{ \ x=1 \ }\)
増減表を書くと
\(\small{ \ \begin{array}{c|ccc}
x & \cdots & 1 & \cdots\\
\hline
y’ & + & 0 & + \\
\hline
y & \nearrow & 1 & \nearrow
\end{array} \ }\)

Point 三次関数のグラフと極大・極小
①微分して\(\small{ \ f'(x)=0 \ }\)を満たす\(\small{ \ x \ }\)の値を求める
②増減表を書いてグラフを正確に書く
\(\small{ \ 2 \ }\)つの関数\(\small{ \ f(x)=2x^3-3x^2-12x \ }\),\(\small{ \ g(x)=-9x^2+6x+a \ }\)に対して次の問いに答えよ。ただし,\(\small{ \ a \ }\)は定数とする。
(1)\(\small{ \ f(x) \ }\)の極大値および極小値を与える\(\small{ \ x \ }\)の値をそれぞれ\(\small{ \ \alpha \ }\),\(\small{ \ \beta \ }\)とおく。\(\small{ \ \alpha \ }\)および\(\small{ \ \beta \ }\)を求めよ。
(2)任意の\(\small{ \ x \gt \alpha \ }\)に対して,\(\small{ \ f(x) \geqq g(x) \ }\)を満たす\(\small{ \ a \ }\)の値の範囲を求めよ。
(1)\(\small{ \ f(x)=2x^3-3x^2-12x \ }\)より
\(\small{ \ f'(x)=6x^2-6x-12\\
=6(x+1)(x-2) \ }\)
よって\(\small{ \ f(x)\ }\)の増減は次のようになる。
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 2 & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 7 & \searrow & -20 & \nearrow
\end{array} \ }\)
よって\(\small{ \ \alpha=-1, \ \beta=2 \ }\)
(2)\(\small{ \ f(x) \geqq g(x) \ }\)
\(\small{ \ 2x^3-3x^2-12x \geqq -9x^2+6x+a \ }\)
\(\small{ \ 2x^3+6x^2-18x \geqq a \cdots① \ }\)
\(\small{ \ ① \ }\)が\(\small{ \ x \gt -1 \ }\)で成り立つ条件は
\(\small{ \ h(x)=2x^3+6x^2-18x \ }\)とすると\(\small{ \ x \gt -1 \ }\)で\(\small{ \ h(x) \ }\)の最小値が\(\small{ \ a \ }\)以上になればよい。
\(\small{ \ h'(x)=6x^2+12x-18=6(x+3)(x-1) \ }\)より\(\small{ \ h(x) \ }\)の増減は次のようになる。
\(\small{ \ \begin{array}{c|ccccc}
x & -1 & \cdots & 1 & \cdots \\
\hline
f’(x) & & – & 0 & + \\
\hline
f(x) & & \searrow & -10 & \nearrow
\end{array} \ }\)
よって求める\(\small{ \ a \ }\)の範囲は\(\small{ \ a \leqq -10 \ }\)

