こんにちは、リンス(@Lins016)です。
今回は2つの曲線に共通な接線の方程式(共通接線)について学習していこう。
2つの曲線に共通な接線は、2つの曲線が接する場合と直線が別の点で2つの曲線に接する場合の2パターンある
2つの曲線が接する場合、その共有点の接線は両方の曲線に接するから、それを式にして接点を求めよう。また、2つの曲線上の異なる2点での接線が等しい場合は各曲線上の点を文字でおいて接線の方程式を出して、それが等しいって式を作って接点を求めよう。
①2つの曲線が接する
\(\small{ \ f(t)=g(t) \ }\)かつ\(\small{ \ f'(t)=g'(t) \ }\)
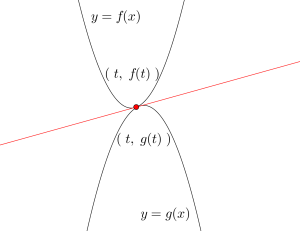
②直線が別の点で2つの曲線に接する
\(\small{ \ y=f'(t)(x-t)+f(t) \ }\)と\(\small{ \ y=g'(s)(x-s)+g(s) \ }\)が一致

曲線が接する問題の解き方
曲線が接する条件は、共有点での接線の傾きが等しいってことになるから、これを式にしていけばいいよね。つまり\(\small{ \ y=f(x) \ }\)と\(\small{ \ y=g(x) \ }\)が接するとき、\(\small{ \ f(t)=g(t) \ }\)かつ\(\small{ \ f'(t)=g'(t) \ }\)を満たす\(\small{ \ t \ }\)を求めよう。・・・・ってなんかこの2つの式だけ見ると\(\small{ \ t \ }\)の方程式だから共有点の式だけで解けそうな気がするけど、問題文には片方の曲線に\(\small{ \ a \ }\)とかの定数が含まれているから\(\small{ \ t \ }\)と\(\small{ \ a \ }\)の連立方程式を解くことになるんだ。
直線が別の点で2つの曲線に接する問題の解き方
この場合は各曲線上の接点を\(\small{ \ t \ }\)と\(\small{ \ s \ }\)などの2つの文字でおいて、その点における接線の方程式をそれぞれ出して、その接線の傾きと\(\small{ \ y \ }\)切片が等しいって式から連立方程式を解こう。2つの接線が全く同じ式だったときに共通接線って言えるよね。また、曲線の1つが2次関数だった場合は判別式も利用できることを覚えておこう。1つの曲線上の点をおいて接線を求め、それがもう1つの曲線(2次関数)に接するから判別式を利用って解法が問題集なんかを解いた時に利用してある場合もあるからね。
(1)\(\small{ \ 2 \ }\)つの曲線\(\small{ \ y=x^2 \ }\)と\(\small{ \ y=-x^2+ax-2 \ }\)が接するとき、\(\small{ \ a \ }\)の値を求めよ。
(2)\(\small{ \ xy \ }\)平面上に\(\small{ \ 2 \ }\)つの曲線\(\small{ \ y=x^3+3 \ }\)と\(\small{ \ y=x^3-1 \ }\)がある。
この\(\small{ \ 2 \ }\)つの曲線のどちらにも接する直線の方程式を求めよ。
(1)接する点の\(\small{ \ x \ }\)座標を\(\small{ \ t \ }\)とすると
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
2t=-2t+a \\
t^2=-t^2+at-2
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ t=\pm1、a=\pm4 \ }\)
(2)\(\small{ \ f(x)=x^3+3、 g(x)=x^3-1 \ }\)とすると
\(\small{ \ (t,f(t)) \ }\)における接線の方程式は
\(\small{ \ y=f'(t)(x-t)+f(t)=3t^2x-2t^3+3 \ }\)
\(\small{ \ (s,g(s)) \ }\)における接線の方程式は
\(\small{ \ y=g'(s)(x-s)+g(s)=3s^2x-2s^3-1 \ }\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
3t^2=3s^2\\
-2t^3+3=-2s^3-1
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ t=1、s=-1 \ }\)
よって求める直線の方程式は\(\small{ \ y=3x+1 \ }\)

Point
①曲線が接するときは共有点で接線の傾きが等しいことを利用
②別の2点で直線に接するときは、曲線上のそれぞれの接点を\(\normalsize{ \ (t,f(t))、(s,g(s)) \ }\)として接線の方程式を作成して、傾きと\(\normalsize{ \ y \ }\)切片が等しいことを利用
\(\small{ \ a \ }\)を正の定数とし、\(\small{ \ 2 \ }\)つの、曲線\(\small{ \ C_1 \ }\)、\(\small{ \ C_2 \ }\)を次のように定める。
\(\small{ \ C_1: \ y=x^3-3x \ }\)
\(\small{ \ C_2: \ y=x^3-3x+a \ }\)
(1) \(\small{ \ C_1 \ }\)と\(\small{ \ C_2 \ }\)の両方に接する直線はただ一つ存在することを示せ。
(2)\(\small{ \ C_1 \ }\)と\(\small{ \ C_2 \ }\)の両方に接する直線を\(\small{ \ l \ }\)とする。\(\small{ \ l \ }\)と \(\small{ \ C_1 \ }\)の\(\small{ \ 2 \ }\)つの共有点の\(\small{ \ x \ }\)座標の差が\(\small{ \ 1 \ }\)になるとき、\(\small{ \ a \ }\)の値を求めよ。
(1)\(\small{ \ C_1 \ }\)上の点 \(\small{ \ (t, \ t^3-3t) \ }\)における接線の方程式は
\(\small{ \ y=(3t^2-3)(x-t)+t^3-3t\\
=(3t^2-3)x-2t^3 \ }\)
\(\small{ \ C_2 \ }\)上の点 \(\small{ \ (s, \ s^3-3s+a) \ }\)における接線の方程式は
\(\small{ \ y=(3s^2-3)(x-s)+s^3-3s+a\\
=(3s^2-3)x-2s^3+a \ }\)
この\(\small{ \ 2 \ }\)つの接線が一致するとき
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
3t^2-3=3s^2-3\\
-2t^3=-2s^3+a
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ (t+s)(t-s)=0\\
a=2(s^3-t^3) \ }\)
\(\small{ \ t=s \ }\)のとき、\(\small{ \ a=0 \ }\)より不適
よって \(\small{ \ t=-s \ }\)
\(\small{ \ a=4s^3 \ }\)
\(\small{ \ s=\sqrt[3 \ ]{ \displaystyle \frac{a}{4} } \ }\)
よって直線の方程式は
\(\small{ \ y=\left(\displaystyle \frac{3}{2}\sqrt[3 ]{ \displaystyle \frac{a^2}{2} }-3\right)x+\displaystyle \frac{a}{2} \ }\)
となり、ただ一つ存在する
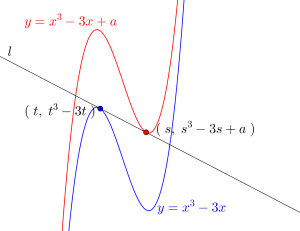
(2)曲線\(\small{ \ C_1 \ }\)と直線\(\small{ \ l \ }\)の交点の\(\small{ \ x \ }\)座標は
\(\small{ \ x^3-3x=(3t^2-3)x-2t^2 \ }\)
\(\small{ \ x^3-3t^2x+2t^2=0 \ }\)
\(\small{ \ (x-t)^2(x+2t)=0 \ }\)
\(\small{ \ x=t, \ -2t \ }\)
よってこの差が\(\small{ \ 1 \ }\)になればよいので
\(\small{ \ t-(-2t)=1 \ }\)
\(\small{ \ t=-\displaystyle \frac{1}{3} \ }\)
(1)より \(\small{ \ t=-s=-\sqrt[3 ]{ \displaystyle \frac{a}{4} } \ }\)
よって \(\small{ \ a=\displaystyle\frac{4}{27} \ }\)

