こんにちは、リンス(@Lins016)です。
今回は3次方程式の解の個数の求め方(基本)について学習していこう。
3次方程式の解の個数は極値で決定
3次方程式の解の個数はグラフと\(\small{ \ x \ }\)軸との交点の個数を調べればいいから、増減表からグラフを書いて\(\small{ \ x \ }\)軸との交点の数を調べよう。
異なる3つの解を持つ場合
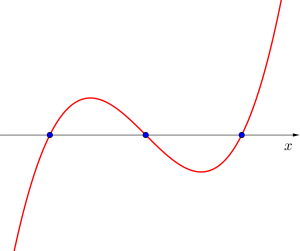
異なる実数解を2つ持つ場合
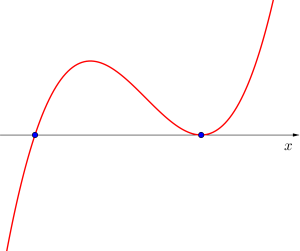
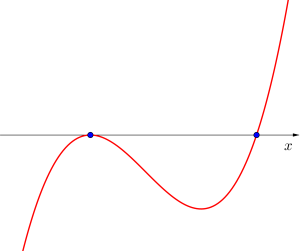
異なる実数解を1つ持つ場合
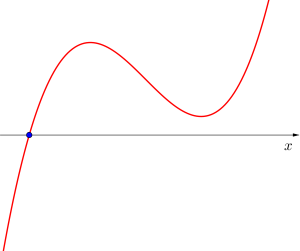
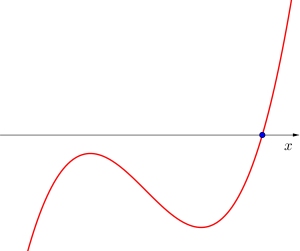
グラフを見てわかる通り解の個数は極大値と極小値の値によって変化してることがわかるよね。極大値と極小値が同符号なら解は1個、極大値と極小値が異符号なら解は3個、極大値と極小値のどちらかが0なら解は2個になる。
3次方程式の解
3次方程式の解の公式って学校では教わらないけどカルダノの公式って呼ばれるものがあるんだ。でも実際それを使って問題を解くことはないから覚える必要はない。しかもめちゃくちゃ長い公式で覚えるのも大変だからね。まず3次方程式を解く場合は高次方程式の解き方を利用して定数項の約数を代入して0になる約数を求めるっていうのがセオリーなんだけど、それはあくまで約数が解になっているものにしか使えないから、それ以外の3次方程式を解けって問題は出てこない。だから3次方程式は解を求めるより、解の個数を求める問題が多いんだ。
次の方程式の異なる実数解の個数を求めよ。
(1)\(\small{ \ x^3-6x^2+9x=0 \ }\)
(2)\(\small{ \ x^3-3x+1=0 \ }\)
(1)\(\small{ \ x^3-6x^2+9x=0 \ }\)
\(\small{ \ x(x-3)^2=0 \ }\)
\(\small{ \ \therefore x=0, \ 3 \ }\)
よって異なる解は\(\small{ \ 2 \ }\)個
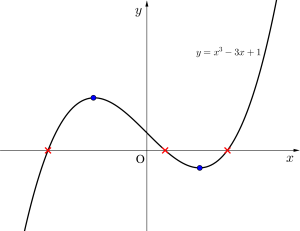
(2)\(\small{ \ f(x)=x^3-3x+1 \ }\)とすると
\(\small{ \ f'(x)=3x^2-3=3(x-1)(x+1) \ }\)より
増減表は
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 1 & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 3 & \searrow & -1 & \nearrow
\end{array} \ }\)
グラフより異なる実数解の個数は\(\small{ \ 3 \ }\)個
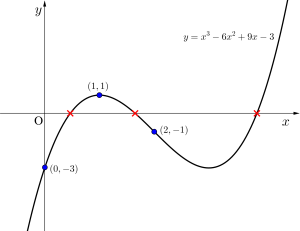
次の方程式が与えられた区間で実数解を持つことを示せ。
\(\small{ \ x^3-6x^2+9x-3=0 \ }\) \(\small{ \ 0\leqq x \leqq 1, \ 1 \leqq x \leqq 2 \ }\)
\(\small{ \ f(x)=x^3-6x^2+9x-1 \ }\)とすると
\(\small{ \ f(0)=-3, \ f(1)=1, \ f(2)=-1 \ }\)より
\(\small{ \ f(x) \ }\)は連続な関数で\(\small{ \ f(1)\lt0, \ f(1) \gt 0, \ f(2)\lt 0 \ }\)より
\(\small{ \ 0\leqq x \leqq 1, \ 1 \leqq x \leqq 2 \ }\)で\(\small{ \ x^3-6x^2+9x-3=0 \ }\)は解を持つ。

Point
①3次方程式の解の個数はグラフと\(\small{ \ x \ }\)軸の交点の数を調べる
②極大値・極小値の値が重要

