共分散と相関係数

こんにちは、リンス(@Lins016)です。
今回は共分散と相関係数について学習していこう。

データの相関関係を調べよう

二つの変量のデータの一方が増えるともう片方も増える(または滅る)傾向が認められるとき、二つの変量の間に正の(負の)相関関係があるってことになる。
今回はこの相関関係を考えてみよう。

共分散とは

二つの変量\(\small{ \ x \ }\)、\(\small{ \ y \ }\)を持つ\(\small{ \ n \ }\)個のデータがあって、\(\small{ \ (x_1,y_1), \ (x_2,y_2), \ \cdots, \ (x_n,y_n) \ }\)とする。
このデータの相関関係を調べるときは、まず\(\small{ \ x \ }\)、\(\small{ \ y \ }\)のデータの平均値をそれぞれ求めよう。

その平均を\(\small{ \ \overline{x} \ }\)、\(\small{ \ \overline{y} \ }\)とすると、\(\small{ \ x \ }\)の偏差と\(\small{ \ y \ }\)の偏差の積\(\small{ \ (x-\overline{x})(y-\overline{y}) \ }\)を各データ計算することで相関関係を調べることができるんだ。

まずは次の三つの散布図を確認してみよう。

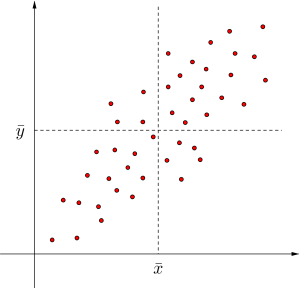
偏差の積が正の値になるのは、\(\small{ \ x \ }\)、\(\small{ \ y \ }\)が「ともに平均より大きい場合」か「ともに平均より小さい場合」になるよね。

偏差の積が負の値になるのは、\(\small{ \ x \ }\)、\(\small{ \ y \ }\)が「片方が平均より大きくてもう片方は平均より小さい場合」になるよね。

つまり散布図が右肩上がりだと共分散が正、右肩下がりだと共分散が負ってことになるんだ。

だからこの偏差の積を全てのデータ調べて、その平均値を求めることで相関関係が求められそうだよね。

この偏差の積の平均値を共分散といい、\(\small{ \ s_{xy} \ }\)で表すから覚えておこう。多分試験に出題される重要な計算式だからね。

共分散の計算

共分散は\(\small{ \ x \ }\)の偏差と\(\small{ \ y \ }\)の偏差の積\(\small{ \ (x-\overline{x})(y-\overline{y}) \ }\)の平均値だからそれ計算すればいいんだけど、与えられたデータの数値によっては次の計算式でも求めることができるから、計算の方法を覚えておこう。

この式は次の式変形から証明することができる。
\(\small{ \ (x_k- \overline{x})(y_k- \overline{y})\\
=x_ky_k- \overline{y}x_k- \overline{x}y_k+ \overline{x}\hspace{ 0.7pt }\overline{y} \ }\)

この\(\small{ \ k \ }\)に\(\small{ \ 1 \ }\)から\(\small{ \ n \ }\)まで代入した式をそれぞれ足すと

ここで、
\(\small{ \ x_1+x_2+\cdots+x_n=n \overline{x} \ }\)
\(\small{ \ y_1+y_2+\cdots+y_n=n \overline{y} \ }\)より、
\(\small{ \ \overline{y}(x_1+x_2+\cdots+x_n)=n\overline{x}\hspace{ 0.7pt }\overline{y} \ }\)
\(\small{ \ \overline{x}(y_1+y_2+\cdots+y_n)=n\overline{x}\hspace{ 0.7pt }\overline{y} \ }\)

分散を求める計算と同じで、与えられたデータによってどちらの式を使うかうまく考えていこう。

相関関係の強さ

例えば、テストの点数について考えてみよう。
テストの点数と勉強時間の相関だと、勉強時間が多いとテストの点数も良さそうじゃない？

中にはたくさん勉強しても点数が取れない人もいると思うけど、たくさんのデータをとるとテストの点数が良いと勉強時間が長いっていう正の相関関係がありそうだよね。

しかも勉強時間はテストの点数に直結するだろうから、かなり強い相関ってことになりそう。

逆にテストの点数とゲームをする時間の相関を考えると、ゲームの時間が長いとテストの点数が悪そうだから負の相関がありそうだよね。

でも、ゲームをしなかったとしても勉強しないとテストで高得点をとれないよね。

だから、テストの点数とゲームをする時間は負の相関があったとしてもそれほど強い相関ではなさそうだよね。

つまりこの例のように相関関係があったとして、それがどれくらいの強さの相関関係になっているのかってことも調べる必要があるんだ。

何となく相関関係がありそうだなぁ〜じゃダメだからね。
それじゃ相関関係の強さを求める式を確認していこう。

相関係数

共分散は、テストの点数と勉強時間のように単位が違う変数を比較する場合、二変数の大きさを測る尺度としてあまりおすすめできないんだよね。だって二変数の単位が違うから、共分散の単位はめちゃくちゃになるしね。

さらに「テストの点数と勉強時間の相関」と「テストの点数とゲームをする時間の相関」を比較する場合、勉強時間の散らばり具合とゲームをする時間の散らばり具合も違うから、共分散を計算してもそれだけで比較するのは難しそうだよね。

だから二つのデータの散らばり具合を同じ尺度にするために、それぞれのデータの標準偏差を求めて、共分散をその積で割ればいいんだ。

そうすることで散らばり具合が同じになるし、標準偏差の単位と偏差の単位は同じだから、共分散の単位がなくなって、複数の相関関係の強さを比較することができるんだ。

この共分散を二変数のそれぞれの標準偏差の積で割った値を相関係数というから覚えておこう。

相関係数は
\(\small{ \ r=\displaystyle \frac{s_{xy}}{s_xy_x} \ }\)
\(\small{ \ s_x \ }\)は\(\small{ \ x \ }\)の標準偏差、\(\small{ \ s_y \ }\)は\(\small{ \ y \ }\)の標準偏差
の式で表され、正の相関関係があるとき\(\small{ \ r\gt0 \ }\)、負の相関関係があるとき\(\small{ \ r\lt0 \ }\)になる。
ただ\(\small{ \ -0.2 \lt r \lt 0.2 \ }\)ぐらいだと相関関係はほとんどないと言えるからね。

あと相関係数は\(\small{ \ -1 \leqq r \leqq 1 \ }\)の範囲になるから\(\small{ \ r \ }\)がこの範囲の値にならなかったら計算ミスしているからもう一度計算し直そう。

相関係数は二つの変数の平均値、標準偏差に加えて共分散を求める必要があるから、計算量がかなり多くなって大変だけど丁寧に計算しよう。
平均値とか何か一つの値が間違ってると全ての値が変わっちゃうから気をつけよう。

また、この例題のように表を利用する問題の場合、平均値を求めたら表に偏差を書き込もう。
この解答のようにわざわざ行を作らなくても小さく横に書けばいいから、まずは偏差の和が\(\small{ \ 0 \ }\)になるか確認しよう。\(\small{ \ 0 \ }\)になったら平均値があってるって確認にもなるからね。

それに偏差は標準偏差や共分散を求める計算にも使うから、この問題のように偏差が整数になる場合は、書いて残しておく方がいいよね。

少しでも計算を簡単にできるように工夫しよう。

Point

①相関の関係は相関係数で求めよう。
②相関係数は共分散、二つの変数の標準偏差を正確に求めて計算しよう。