こんにちは、リンス(@Lins016)です。
今回は二次方程式と判別式について学習していこう。
複素数範囲での二次方程式と判別式
数学Iで判別式を教わったけど、あの時ってまだ虚数のことを知らなかったよね。
今回は複素数範囲まで考えた二次方程式の判別式について考えていこう。
-

判別式とその利用
判別式について学習してます。解の個数や、グラフとx軸の共有点の数の求め方、不等式の作成について解説しています。
続きを見る
\(\small{ \ ax^2+bx+c=0 \ }\)
解の公式より\(\small{ \ x=\displaystyle\frac{-b\pm\sqrt{b^2-4ac}}{2a} \ }\)
この二次方程式の判別式を\(\small{ \ D \ }\)とすると
\(\small{ \ D=b^2-4ac \ }\)より
\(\small{ \ x=\displaystyle\frac{-b\pm\sqrt{D}}{2a} \ }\)
よって
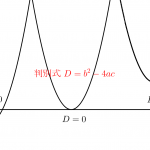
\(\small{ \ D\gt0 \ }\)で異なる二つの実数解
\(\small{ \ D=0 \ }\)で重解(実数解)
\(\small{ \ D\lt0 \ }\)で異なる二つの虚数解
判別式
数学Iで教わった二次方程式\(\small{ \ ax^2+bx+c=0 \ }\)の判別式\(\small{ \ D=b^2-4ac \ }\)は
\(\small{ \ D\gt0 \ }\)で異なる二つの解
\(\small{ \ D=0 \ }\)で重解
\(\small{ \ D\lt0 \ }\)で解なし
ってことになってたよね。
\(\small{ \ ax^2+bx+c=0 \ }\)の解は\(\small{ \ x=\displaystyle\frac{-b\pm\sqrt{D}}{2a} \ }\)だから、実数の範囲だとルートの中がマイナスになる数は存在しないから、\(\small{ \ D\lt0 \ }\)は解なしになるよね。
でも実数の範囲ならこれでいいんだけど、複素数の範囲まで考えると、
\(\small{ \ D\gt0 \ }\)で異なる二つの実数解
\(\small{ \ D=0 \ }\)で重解(実数解)
\(\small{ \ D\lt0 \ }\)で異なる二つの虚数解
になる。
複素数には虚数\(\small{ \ \sqrt{-1}=i \ }\)が存在するから、ルートの中がマイナスになってもいいんだよね。
つまり複素数の範囲まで考えると二次方程式は必ず解をもつってことになる。
ただ、あくまでも複素数の範囲まで考えた場合ね。
前も話したように高校数学ではほとんどの単元で実数の範囲までしか考えない。
だから今回学習している「複素数と方程式」や数学Ⅲの「複素数平面」では複素数の範囲まで考えるけど、それ以外の単元では虚数解は解なしになるから気をつけよう。
\(\small{ \ k \ }\)は実数の定数とする。次の方程式の解の種類を判別せよ。
\(\small{ \ (k-1)x^2+4x+2k=0 \ }\)
\(\small{ \ k-1\neq 0 \ }\)のときこの方程式は二次方程式だから
判別式を\(\small{ \ D \ }\)とすると
\(\small{\begin{eqnarray} \ D&=&4^2-4(k-1)\cdot2k\\
&=&-8k^2+8k+16\\
&=&-8(k+1)(k-2) \ \end{eqnarray}}\)
\(\small{ \ D\gt0 \ }\)のとき
\(\small{ \ \therefore -1\lt k \lt1, \ 1 \lt k \lt 2 \ }\)のとき実数解\(\small{ \ 2 \ }\)個
\(\small{ \ D=0 \ }\)のとき
\(\small{ \ \therefore k=-1, \ 2 \ }\)のとき重解
\(\small{ \ D\lt0 \ }\)のとき
\(\small{ \ \therefore k\lt-1, k\gt 2 \ }\)のとき虚数解\(\small{ \ 2 \ }\)個
\(\small{ \ k=1 \ }\)のとき\(\small{ \ 4x+2=0 \ }\)より実数解\(\small{ \ 1 \ }\)個

問題文に「二次方程式\(\small{ \ ax^2+bx+c=0 \ }\)」って書いてあれば\(\small{ \ a\neq0 \ }\)ってことになるけど、「方程式\(\small{ \ ax^2+bx+c=0 \ }\)」って書いてあれば\(\small{ \ a=0 \ }\)と\(\small{ \ a\neq0 \ }\)の場合わけが必要になるからね。
\(\small{ \ a=0 \ }\)の場合は二次方程式じゃなくて一次方程式になるから注意しよう。
複素数係数の方程式が実数解をもつ条件
複素数係数の方程式では判別式が使えない。
だから複素数係数の方程式の問題で「次の二次方程式が実数解をもつような\(\small{ \ k \ }\)の値を求めよ」っていうのに判別式を利用したらだめだからね。
複素数係数の方程式のほとんどの問題で「実数解をもつ」ってヒントが与えられてるから、実数解をもつってところをきちんと考えてみよう。
複素数係数の方程式が実数解をもつってことは、この方程式は\(\small{ \ (x-2)(x-3+i)=0 \ }\)のような形をしていることがほとんどなんだ。
これを展開すると\(\small{ \ x^2-(5-i)x+6-2i=0 \ }\)になって係数が複素数(実数と虚数)になってるよね。
これに対して、実数解が二つの方程式や虚数解二つ(共役)の解を持つ方程式は
\(\small{ \ (x-2)(x+4)=0 \ }\)や\(\small{ \ (x-1+i)(x-1-i)=0 \ }\)のような形になって、これを展開するとその方程式は、
\(\small{ \ x^2+2x-8=0 \ }\)と\(\small{ \ x^2-2x+2=0 \ }\)になって複素数係数ではなく、実数係数になってしまうからね。
つまり複素数係数の方程式は
\(\small{ \ (x-r)(x-p-qi)=0 \ }\)(\(\small{ \ p, \ q, \ r \ }\)は実数)の形だから、まずは実数解\(\small{ \ x=r \ }\)を求めるようにしよう。
そのためには\(\small{ \ a, \ b \ }\)が実数のとき\(\small{ \ a+bi=0 \ }\)なら\(\small{ \ a=b=0 \ }\)を利用して実数解を求めよう。
二次方程式\(\small{ \ x^2+(a+i)x-2(1+i)=0 \ }\)(\(\small{ \ i \ }\)は虚数単位)が実数解を持つとき実数\(\small{ \ a \ }\)とこの二次方程式の解を求めよ。
\(\small{ \ x^2+(a+i)x-2(1+i)=0 \ }\)
この方程式の実数解を\(\small{ \ m \ }\)とすると
\(\small{ \ m^2+(a+i)m-2(1+i)=0 \ }\)
\(\small{ \ m^2+am-2+(m-2)i=0 \ }\)
\(\small{ \ a, \ m \ }\)ともに実数より
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
m^2+am-2=0 \\
m-2=0
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ m=2, \ a=-1 \ }\)
これを\(\small{ \ x^2+(a+i)x-2(1+i)=0 \ }\)に代入すると
\(\small{ \ x^2+(-1+i)x-2(1+i)=0 \ }\)
\(\small{ \ (x-2)(x+1+i)=0 \ }\)
\(\small{ \ \therefore x=2, \ -1-i \ }\)
よって\(\small{ \ a=-1 \ \ x=2, \ -1-i \ }\)

「\(\small{ \ a, \ b \ }\)が有理数のとき\(\small{ \ a+b\sqrt{3}=0 \ }\)なら\(\small{ \ a=b=0 \ }\)」が成り立つっていうのもあるから合わせて覚えておこう。
Point 二次方程式と判別式
①複素数の範囲まで考える場合の判別式は、実数解か虚数解を必ずもつ
②複素数係数の方程式が実数解をもつ問題は判別式じゃなくて\(\small{ \ a, \ b \ }\)が実数のとき\(\small{ \ a+bi=0 \ }\)なら\(\small{ \ a=b=0 \ }\)を利用しよう