こんにちは、リンス(@Lins016)です。
今回は1/6公式を利用した面積の問題について学習していきましょう。
1/6公式を利用した様々な問題とその解き方
\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式を利用した様々な問題について学習していく前に、どんな形で\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式が使えるのか確認しておこう。
-

面積と1/6公式
1/6公式が利用できるパターンについて詳しく解説しています。
続きを見る
今回は定期試験対策としてどんな問題があって、その解き方はどうするのかを確実に押さえていこう。
\(\small{ \ \displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=-\displaystyle\frac{1}{6}(\beta-\alpha)^3 \ }\)
\(\small{ \ \displaystyle\int_{\alpha}^{\beta}a(x-\alpha)(x-\beta)dx=-\displaystyle\frac{a}{6}(\beta-\alpha)^3 \ }\)

放物線とx軸で囲まれた面積を二等分する問題
まずは「放物線と\(\small{ \ x \ }\)軸で囲まれた面積を二等分する直線を求める問題」について考えていこう。
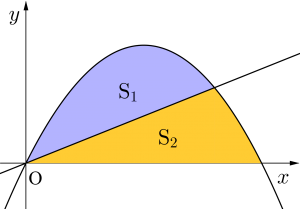
図のように放物線と\(\small{ \ x \ }\)軸で囲まれた面積を\(\small{ \ \mathrm{S} \ }\)とすると、まず\(\small{ \ \mathrm{S} \ }\)に\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式が使えるよね。
次に二等分する直線と放物線で囲まれた面積を\(\small{ \ \mathrm{S}_1 \ }\)っておくと\(\small{ \ \mathrm{S}_1 \ }\)にも\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式が使えるよね。
二等分された面積は\(\small{ \ \mathrm{S}_1 \ }\)も\(\small{ \ \mathrm{S}_2 \ }\)も同じ面積だから\(\small{ \ \mathrm{S}_2 \ }\)を求めてもいいけど、\(\small{ \ \mathrm{S}_2 \ }\)は三本で囲まれた面積だから\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式も使えないし、面積を求めるためには図を二つに分割して求めないといけないから大変だよね。

\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式が使える簡単な方の面積を求めるようにしよう。
\(\small{ \ y=-x^2+2x \ }\)と\(\small{ \ x \ }\)軸で囲まれた面積を\(\small{ \ y=mx \ }\)が二等分するとき\(\small{ \ m \ }\)の値を求めよ。
\(\small{ \ y=-x^2+2x \ }\)と\(\small{ \ x \ }\)軸の共有点は
\(\small{ \ -x^2+2x=0 \ }\)
\(\small{ \ x(x-2)=0 \ }\)
\(\small{ \ x=0, \ 2 \ }\)
\(\small{ \ y=-x^2+2x \ }\)と\(\small{ \ x \ }\)軸で囲まれた面積\(\small{ \ \mathrm{S} \ }\)は
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\int_{0}^{2}(-x^2+2x)dx\\
&=&\displaystyle\int_{0}^{2}-x(x-2)dx\\
&=&\displaystyle\frac{1}{6}\cdot2^3=\displaystyle\frac{4}{3} \ \end{eqnarray}}\)
\(\small{ \ y=-x^2+2x \ }\)と\(\small{ \ y=mx \ }\)の共有点は
\(\small{ \ -x^2+2x=mx \ }\)
\(\small{ \ x(x-2+m)=0 \ }\)
\(\small{ \ x=0, \ 2-m \ }\)
ただし図形を二等分するためには
\(\small{ \ 0\lt 2-m \lt 2 \ }\)
\(\small{ \ \therefore 0 \lt m \lt 2 \ }\)
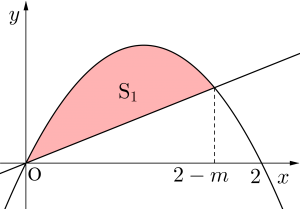
\(\small{ \ y=-x^2+2x \ }\)と\(\small{ \ y=mx \ }\)で囲まれた面積\(\small{ \ \mathrm{S}_1 \ }\)は
\(\small{\begin{eqnarray} \ \mathrm{S}_1&=&\displaystyle\int_{0}^{2-m}(-x^2+2x-mx)dx\\
&=&\displaystyle\int_{0}^{2-m}-x(x-2+m)dx\\
&=&\displaystyle\frac{1}{6}\cdot(2-m)^3 \ \end{eqnarray}}\)
\(\small{ \ \mathrm{S}_1=\displaystyle\frac{1}{2}\mathrm{S} \ }\)より
\(\small{ \ \displaystyle\frac{1}{6}(2-m)^3=\displaystyle\frac{2}{3} \ }\)
\(\small{ \ 2-m=\sqrt[3]{4} \ }\)
\(\small{ \ m=2-\sqrt[3]{4} \ }\)
これは\(\small{ \ 0\lt m \lt 2 \ }\)を満たす

定点を通る直線と放物線の囲む面積の最小値の問題
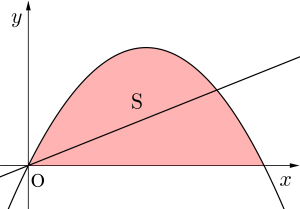
次に「ある定点を通る直線と放物線の囲む面積の最小値を求める問題」について考えていこう。
図の赤い点(定点)を通る二つの直線(赤い直線と青い直線)が放物線と囲むそれぞれの面積は大きさが異なることがわかるよね。
定点と放物線が与えられていて、その定点を通る直線の傾きが変化すると直線と放物線で囲まれた面積も変化するんだ。

ってことは面積は傾きを変数とする関数で表すことができそうだよね。関数ってことは最大最小問題になるってこと。
今回はこの面積の最小値を求めるんだけど、この面積も直線と放物線の二本で囲まれてるから\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式が使えるよね。
ただ今回注意しないといけないのは積分区間も直線の傾きによって変化するから、積分区間にも直線の傾きの定数が入るんだ。
そのことに注意しながら例題を解いていこう。
放物線\(\small{ \ y=x^2+x \ }\)と\(\small{ \ (0, \ 1) \ }\)を通る傾き\(\small{ \ a \ }\)の直線とで囲まれた面積\(\small{ \ \mathrm{S} \ }\)の最小値とそのときの\(\small{ \ a \ }\)の値を求めよ。
\(\small{ \ (0, \ 1) \ }\)を通る傾き\(\small{ \ a \ }\)の直線の方程式は\(\small{ \ y=ax+1 \ }\)
放物線と直線の共有点は
\(\small{ \ x^2+x=ax+1 \ }\)
\(\small{ \ x^2+(1-a)x-1=0 \ }\)

ここでこの方程式の解を\(\small{ \ x=\alpha, \ \beta(\alpha \lt \beta) \ }\)とすると
求める面積は
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\int_{\alpha}^{\beta}\left\{(ax+1)-(x^2+x)\right\}dx\\
&=&\displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx\\
&=&\displaystyle\frac{1}{6}(\beta-\alpha)^3 \ \end{eqnarray}}\)
ここで\(\small{ \ \alpha, \ \beta \ }\)は解と係数の関係より
\(\small{ \ \alpha+\beta=a-1 \ }\)
\(\small{ \ \alpha\beta=-1 \ }\)
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\frac{1}{6}(\beta-\alpha)^3\\
&=&\displaystyle\frac{1}{6}\left\{(\beta-\alpha)^2\right\}^{\displaystyle\frac{3}{2}}\\
&=&\displaystyle\frac{1}{6}\left\{(\beta+\alpha)^2-4\alpha\beta\right\}^{\displaystyle\frac{3}{2}}\\
&=&\displaystyle\frac{1}{6}\left\{(a-1)^2+4\right\}^{\displaystyle\frac{3}{2}} \ \end{eqnarray}}\)
よって面積が最小になるのは\(\small{ \ a=1 \ }\)のとき
最小値\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{6}4^{\displaystyle\frac{3}{2}}=\displaystyle\frac{4}{3} \ }\)

それにこんな文字を含んだ二次方程式の解を\(\small{ \ \alpha, \ \beta \ }\)っておいて、解と係数の関係を利用するのは入試の鉄則だからね。
二次方程式に定数を含む場合は\(\small{ \ \alpha, \ \beta \ }\)とおくようにしよう。
-

解と係数の関係
解と係数の関係を利用した問題や解と係数の関係の利用について詳しく解説しています。
続きを見る
Point 1/6公式を利用した面積の問題
①放物線と直線で囲まれた面積は\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式を利用する
②積分区間が複雑な値の問題は解と係数の関係を利用する
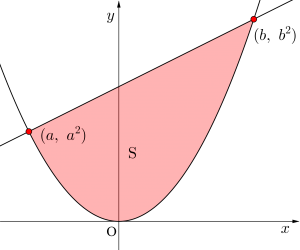
\(\small{ \ a, \ b \ }\)は\(\small{ \ a\lt b \ }\)を満たす実数とし、放物線\(\small{ \ C: y=x^2 \ }\)上の二点\(\small{ \ \mathrm{A}(a, \ a^2) \ }\)、\(\small{ \ \mathrm{B}(b, \ b^2) \ }\)を考える。
(1)直線\(\small{ \ \mathrm{AB} \ }\)の方程式を\(\small{ \ a \ }\)と\(\small{ \ b \ }\)を用いて表せ。
(2)放物線\(\small{ \ C \ }\)と直線\(\small{ \ \mathrm{AB} \ }\)で囲まれた面積\(\small{ \ \mathrm{S} \ }\)を\(\small{ \ a \ }\)と\(\small{ \ b \ }\)を用いて表せ。
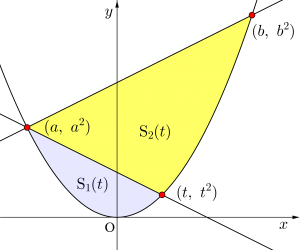
(3)\(\small{ \ a\lt t \lt b \ }\)の範囲で点\(\small{ \ \mathrm{P}(t, \ t^2) \ }\)が動くとき、放物線\(\small{ \ C \ }\)と直線\(\small{ \ \mathrm{AP} \ }\)で囲まれた図形の面積を\(\small{ \ \mathrm{S}_1(t) \ }\)、放物線\(\small{ \ C \ }\)と二直線\(\small{ \ \mathrm{AB}, \ \mathrm{AP} \ }\)で囲まれた図形の面積を\(\small{ \ \mathrm{S}_2(t) \ }\)とする。
このとき\(\small{ \ \mathrm{S}_2(t)=7\mathrm{S}_1(t) \ }\)を満たす\(\small{ \ t \ }\)を\(\small{ \ a \ }\)と\(\small{ \ b \ }\)を用いて表せ。
(1)直線\(\small{ \ \mathrm{AB} \ }\)の方程式は\(\small{ \ \mathrm{A}(a, \ a^2) \ }\)、\(\small{ \ \mathrm{B}(b, \ b^2) \ }\)を通るので
\(\small{ \ y=\displaystyle\frac{b^2-a^2}{b-a}(x-a)+a^2 \ }\)
\(\small{ \ y=(a+b)x-ab \ }\)
(2)求める面積\(\small{ \ \mathrm{S} \ }\)は
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\int_{a}^{b}\left\{(a+b)x-ab-x^2\right\}dx\\
&=&-\displaystyle\int_{a}^{b}(x-a)(x-b)dx\\
&=&\displaystyle\frac{1}{6}(b-a)^3 \ \end{eqnarray}}\)
(3)直線\(\small{ \ \mathrm{AP} \ }\)の方程式は\(\small{ \ \mathrm{A}(a, \ a^2) \ }\)、\(\small{ \ \mathrm{P}(t, \ t^2) \ }\)を通るので
\(\small{ \ y=\displaystyle\frac{t^2-a^2}{t-a}(x-a)+a^2 \ }\)
\(\small{ \ y=(a+t)x-at \ }\)
よって\(\small{ \ \mathrm{S}_1(t) \ }\)は
\(\small{\begin{eqnarray} \ \mathrm{S}_1(t)&=&\displaystyle\int_{a}^{t}\left\{(a+t)x-at-x^2\right\}dx\\
&=&-\displaystyle\int_{a}^{t}(x-a)(x-t)dx\\
&=&\displaystyle\frac{1}{6}(t-a)^3 \ \end{eqnarray}}\)
\(\small{ \ \mathrm{S}_2(t)=\mathrm{S}-\mathrm{S}_1(t) \ }\)より
\(\small{ \ \mathrm{S}_2(t)=\displaystyle\frac{1}{6}(b-a)^3-\displaystyle\frac{1}{6}(t-a)^3 \ }\)
\(\small{ \ \mathrm{S}_2(t)=7\mathrm{S}_1(t) \ }\)より
\(\small{ \ \displaystyle\frac{1}{6}(b-a)^3-\displaystyle\frac{1}{6}(t-a)^3=\displaystyle\frac{7}{6}(t-a)^3 \ }\)
\(\small{ \ 8(t-a)^3=(b-a)^3 \ }\)
\(\small{ \ 2(t-a)=b-a \ }\)
よって\(\small{ \ t=\displaystyle\frac{a+b}{2} \ }\)