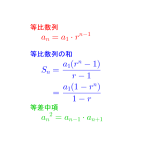こんにちは、リンス(@Lins016)です。
今回は無限等比数列について学習していこう。
無限等比数列
無限等比数列って無限に続く等比数列のこと。
だから等比数列の一般項の極限を考える問題になるんだけど、このとき重要なのは等比数列の公比。
公比の大きさによって無限大に発散したり、収束したりするからね。今回はそのことをしっかりと考えながら、無限等比数列について考えていこう。
その前に等比数列について復習しておこう。
-

等比数列と等比数列の和
公式の確認から等比数列の一般項の求め方について詳しく解説しています。
続きを見る
無限等比数列\(\small{ \ \left\{r^n\right\} \ }\)の極限
・\(\small{ \ r\gt1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=\infty \ }\)
\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{r^n}=0 \ }\)
・\(\small{ \ r=1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=1 \ }\)
・\(\small{ \ -1\lt r \lt 1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=0 \ }\)
・\(\small{ \ r=-1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n \ }\)はない
・\(\small{ \ r\lt-1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n \ }\)はない
\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{r^n}=0 \ }\)
公比によって極限値が異なる
無限等比数列の極限は公比によって異なる。なぜそうなるかということについて考えてみよう。
①\(\small{ \ r\gt1 \ }\)のとき
\(\small{ \ r=1+h \ (h\gt0) \ }\)とすると二項定理を使って
\(\small{\begin{eqnarray} \ r^n&=&(1+h)^n\\[3pt]
&=&_n\mathrm{C}_0+_n\mathrm{C}_1h+_n\mathrm{C}_2h^2+\cdots+_n\mathrm{C}_nh^n\\[3pt]
&=&1+nh+\displaystyle\frac{n(n-1)}{2}h^2+\cdots\\[3pt]
&\geqq&1+nh \ (\because h\gt 0) \ \end{eqnarray}}\)
\(\small{ \ r^n\geqq1+nh \ }\)
\(\small{ \ \displaystyle\lim_{n\to \infty}(1+nh)=\infty \ }\)だから\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=\infty \ }\)
二項定理について忘れている人は確認しておこう。
-

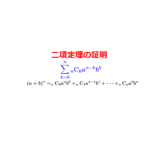
二項定理の証明
数学的帰納法を用いた二項定理の証明について詳しく解説しています。
続きを見る
②\(\small{ \ r=1 \ }\)のとき
\(\small{ \ 1 \ }\)を何度かけても\(\small{ \ 1 \ }\)だから\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=1 \ }\)になるよね。
③\(\small{ \ 0\lt r \lt1 \ }\)のとき
\(\small{ \ r=\displaystyle\frac{1}{t} \ }\)とすると\(\small{ \ t\gt1 \ }\)になるから\(\small{ \ r^n=\displaystyle\frac{1}{t^n} \ }\)
①を利用すると\(\small{ \ \displaystyle\lim_{n\to \infty}t^n=\infty \ }\)だから\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=\displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{t^n}=0 \ }\)
④\(\small{ \ r=0 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=0 \ }\)
これはもういいよね。
⑤\(\small{ \ -1\lt r\lt0 \ }\)のとき
\(\small{ \ r=-t \ }\)とすると\(\small{ \ 0\lt t \lt1 \ }\)、\(\small{ \ \left|r^n\right|=t^n \ }\)
③を利用すると\(\small{ \ \displaystyle\lim_{n\to \infty}t^n=0 \ }\)だから\(\small{ \ \displaystyle\lim_{n\to \infty}\left|r^n\right|=0 \ }\)
このとき\(\small{ \ -\left|r^n\right|\leqq r^n \leqq \left|r^n\right| \ }\)が言えるから
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=0 \ }\)
⑥\(\small{ \ r=-1 \ }\)のとき
数列\(\small{ \ \left\{r^n\right\} \ }\)は\(\small{ \ -1, \ 1, \ -1,\cdots \ }\)と\(\small{ \ -1 \ }\)と\(\small{ \ 1 \ }\)を繰り返すから振動ってことになって極限はなしになる。
⑦\(\small{ \ r\lt -1 \ }\)のとき
\(\small{ \ r=-t \ }\)とすると\(\small{ \ t\gt1 \ }\)、\(\small{ \ r^n=(-1)^nt^n \ }\)、
\(\small{ \ \displaystyle\lim_{n\to \infty}\left|r^n\right|=\displaystyle\lim_{n\to \infty}t^n=\infty \ }\)になるから、数列\(\small{ \ \left\{r^n\right\} \ }\)の項の符号は交互に変わるから、これも振動になって極限はなしになる。
①〜⑦をまとめると
公比と極限値の関係
・\(\small{ \ r\gt1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=\infty \ }\)(発散)
・\(\small{ \ r=1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=1 \ }\)(収束)
・\(\small{ \ -1\lt r \lt 1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=0 \ }\)(収束)
・\(\small{ \ r=-1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n \ }\)はない(振動)
\(\small{ \ r\lt-1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n \ }\)はない(振動)
公比によって極限が異なるから確実に覚えておこう。
数列\(\small{ \ \left\{(x^2-x-1)^n\right\} \ }\)が収束するような\(\small{ \ x \ }\)の範囲を求めよ。
\(\small{ \ \left\{(x^2-x-1)^n\right\} \ }\)が収束するのは
\(\small{ \ -1\lt x^2-x-1\leqq1 \ }\)のとき
\(\small{ \ x^2-x-1\gt-1 \ }\)
\(\small{ \ x(x-1)\gt0 \ }\)
\(\small{ \ x\lt0, \ x\gt1\cdots① \ }\)
\(\small{ \ x^2-x-1\leqq1 \ }\)
\(\small{ \ x-2-x-2\leqq0 \ }\)
\(\small{ \ (x-2)(x+1)\leqq0 \ }\)
\(\small{ \ -1\leqq x\leqq2\cdots② \ }\)
\(\small{ \ ①,② \ }\)より
\(\small{ \ -1\leqq x \lt0, \ 1 \lt x \leqq2 \ }\)
数列の極限と収束
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n \ }\)は極限が異なるから\(\small{ \ r \ }\)の場合分けをする必要があることがわかったけど、これと合わせてもう一つ覚えておいて欲しいことがある。
数列の極限の考え方でも勉強したけど、数列の極限って\(\small{ \ \displaystyle\frac{\infty}{\infty} \ }\)のような場合、分母を収束させると極限が求めやすくなったよね。
発散するよりも収束する方がわかりやすいから、できれば収束するような形に変形をさせたいんだ。
無限大に発散するものは、発散するってことだけ覚えてるんだじゃなくて、分母に持ってくると\(\small{ \ 0 \ }\)に収束するってことまで覚えておこう。
つまり\(\small{ \ r\gt1 \ }\)のとき、\(\small{ \ \displaystyle\lim_{n\to \infty}r^n=\infty \ }\)だったけど、一緒に\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{r^n}=0 \ }\)まで覚えていてほしいってこと。
さらに\(\small{ \ r\lt-1 \ }\)のときも\(\small{ \ \displaystyle\lim_{n\to \infty}r^n \ }\)の極限はなかったけど、分母に持ってくると\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{r^n}=0 \ }\)になるからね。
この形まで確実におさえておこう。
公比と絶対値
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n \ }\)の極限は\(\small{ \ r\gt1 \ }\)、\(\small{ \ r=1 \ }\)、\(\small{ \ -1\lt r\lt1 \ }\)、\(\small{ \ r=-1 \ }\)、\(\small{ \ r\lt-1 \ }\)の\(\small{ \ 5 \ }\)つの場合分けが基本だけど、問題集なんか解いていると、公比\(\small{ \ r \ }\)が\(\small{ \ \left|r\right|\lt1 \ }\)、\(\small{ \ \left|r\right|=1 \ }\)、\(\small{ \ \left|r\right|\gt1 \ }\)の\(\small{ \ 3 \ }\)つの場合分けになってることがある。
\(\small{ \ \left|r\right|\lt1 \ }\)は\(\small{ \ -1\lt r\lt1 \ }\)、\(\small{ \ \left|r\right|=1 \ }\)は\(\small{ \ r=\pm1 \ }\)、\(\small{ \ \left|r\right|\gt1 \ }\)は\(\small{ \ r\gt1, \ r\lt-1 \ }\)を表してるよね。
\(\small{ \ \displaystyle\lim_{n\to \infty}r^n \ }\)の極限を考えると\(\small{ \ r\gt1 \ }\)と\(\small{ \ r\lt-1 \ }\)の極限は異なるんだけど、問題として与えられた式だと\(\small{ \ r\gt1 \ }\)と\(\small{ \ r\lt-1 \ }\)の極限は同じになることがほとんどなんだ。
だってどちらも\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{r^n}=0 \ }\)になるからね。
\(\small{ \ \left|r\right|\lt1 \ }\)は\(\small{ \ -1\lt r\lt1 \ }\)で\(\small{ \ 5 \ }\)つの場合分けと\(\small{ \ 3 \ }\)つの場合分けで同じだからいいけどだけど、\(\small{ \ \left|r\right|=1 \ }\)は\(\small{ \ r=\pm1 \ }\)だから、これは問題によって、きちんと考えないといけない。
\(\small{ \ r=1 \ }\)のときと\(\small{ \ r=-1 \ }\)のときが同じ極限値になるなら\(\small{ \ \left|r\right|=1 \ }\)ってまとめても問題ないし、問題にあらかじめ\(\small{ \ r\neq1 \ }\)って書いてあったら、\(\small{ \ 3 \ }\)つの場合分けでやった方が楽ってこともあるけど、\(\small{ \ r=1 \ }\)のときと\(\small{ \ r=-1 \ }\)のときが同じ極限じゃないならきちんとわけないといけないからね。
まあここで何が言いたかったかというと、\(\small{ \ r\gt1 \ }\)、\(\small{ \ r=1 \ }\)、\(\small{ \ -1\lt r\lt1 \ }\)、\(\small{ \ r=-1 \ }\)、\(\small{ \ r\lt-1 \ }\)の\(\small{ \ 5 \ }\)つの場合分けと\(\small{ \ \left|r\right|\lt1 \ }\)、\(\small{ \ \left|r\right|=1 \ }\)、\(\small{ \ \left|r\right|\gt1 \ }\)の\(\small{ \ 3 \ }\)つの場合で大きく異なるわけじゃないってこと。
問題集の答えが\(\small{ \ 3 \ }\)つの場合分けになっているから、\(\small{ \ 5 \ }\)つの場合分けで解いたらだめってことじゃないからね。
当然\(\small{ \ 5 \ }\)つの場合分けの方が丁寧に分けてるんだから、それで問題ない。だから心配だったら常に\(\small{ \ r\gt1 \ }\)、\(\small{ \ r=1 \ }\)、\(\small{ \ -1\lt r\lt1 \ }\)、\(\small{ \ r=-1 \ }\)、\(\small{ \ r\lt-1 \ }\)の\(\small{ \ 5 \ }\)つの場合分けを使えばいいんだ。
次の極限を調べよ。
(1)\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{2^n-3^n}{2^n+3^n} \ }\)
(2)\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{r^{n+2}+r^{n+1}+1}{r^{n+1}+r-1} \ }\)
(1)\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{2^n-3^n}{2^n+3^n}\\[3pt] =\displaystyle\lim_{n\to \infty}\displaystyle\frac{\left(\textstyle\frac{2}{3}\right)^n-1}{\left(\textstyle\frac{2}{3}\right)^n+1}\\[3pt] =-1 \ }\)
(2)\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{r^{n+2}+r^{n+1}+1}{r^{n+1}+r-1} \ }\)
(i)\(\small{ \ r\gt1, \ r\lt-1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{r^{n+2}+r^{n+1}+1}{r^{n+1}+r-1}\\[3pt]
=\displaystyle\frac{r+1+\textstyle\frac{1}{r^{n+1}}}{1+\textstyle\frac{1}{r^{n}}-\textstyle\frac{1}{r^{n+1}}}\\[3pt]
=r+1 \ }\)
(ii)\(\small{ \ r=1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1^{n+2}+1^{n+1}+1}{1^{n+1}+1-1}\\[3pt]
=3 \ }\)
(iii)\(\small{ \ -1\lt r\lt1 \ }\)のとき
\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{r^{n+2}+r^{n+1}+1}{r^{n+1}+r-1}\\[3pt]
=\displaystyle\frac{1}{r-1} \ }\)
(iv)\(\small{ \ r=-1 \ }\)のとき
\(\small{ \ \displaystyle\frac{(-1)^{n+2}+(-1)^{n+1}+1}{(-1)^{n+1}-1-1}\\[3pt]
\ }\)
よって極限なし
(i)〜(iv)より
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
r+1 \left(r\gt1, \ r\lt-1\right)\\
3 \left(r=1\right)\\
\displaystyle\frac{1}{r-1}\left(-1\lt r\lt1\right)\\
なし(r=-1)
\end{array}
\right.
\end{eqnarray} \ }\)

それに対して\(\small{ \ r=1 \ }\)や\(\small{ \ -1\lt t \lt 1 \ }\)は\(\small{ \ r^n \ }\)が収束するからそのまま変形せずに代入してる。
等比数列の極限だけど結局は数列の極限と同じで、収束する形にしてから極限を求めてることに気付くよね。
極限の問題はこのことを意識して問題を解こう。
Point 無限等比数列
①公比の大きさで極限を考える
②公比が文字なら場合分けする
\(\small{ \ f_n(x)=\displaystyle\frac{\tan^{2n+1}x-\tan^nx+1}{\tan^{2n+2}x+\tan^{2n}x+1} \ }\)\(\small{ \ \left(0\leqq x\lt \displaystyle\frac{\pi}{2}\right) \ }\)とする。
\(\small{ \ f(x)=\displaystyle\lim_{n\to \infty}f_n(x) \ }\)を求めよ。
(i)\(\small{ \ \tan x\lt1 \ }\)
\(\small{ \ \therefore 0 \leqq x \lt \displaystyle\frac{\pi}{4} \ }\)のとき
\(\small{ \ f(x)=\displaystyle\lim_{n\to \infty}f_n(x)\\[3pt]
=\displaystyle\lim_{n\to \infty}\displaystyle\frac{\tan^{2n+1}x-\tan^nx+1}{\tan^{2n+2}x+\tan^{2n}x+1}\\[3pt]
=\displaystyle\frac{0-0+1}{0+0+1}\\[3pt]
=1 \ }\)
(ii)\(\small{ \ \tan x=1 \ }\)
\(\small{ \ \therefore x=\displaystyle\frac{\pi}{4} \ }\)のとき
\(\small{ \ f(x)=\displaystyle\lim_{n\to \infty}f_n(x)\\[3pt]
=\displaystyle\lim_{n\to \infty}\displaystyle\frac{\tan^{2n+1}\textstyle\frac{\pi}{4}-\tan^n\textstyle\frac{\pi}{4}+1}{\tan^{2n+2}\textstyle\frac{\pi}{4}+\tan^{2n}\textstyle\frac{\pi}{4}+1}\\[3pt]
=\displaystyle\frac{1-1+1}{1+1+1}\\[3pt]
=\displaystyle\frac{1}{3} \ }\)
(iii)\(\small{ \ \tan x\gt1 \ }\)
\(\small{ \ \therefore\displaystyle\frac{\pi}{4} \lt x \lt \displaystyle\frac{\pi}{2} \ }\)のとき
\(\small{ \ f(x)=\displaystyle\lim_{n\to \infty}f_n(x)\\[3pt]
=\displaystyle\lim_{n\to \infty}\displaystyle\frac{\tan^{2n+1}x-\tan^nx+1}{\tan^{2n+2}x+\tan^{2n}x+1}\\[3pt]
=\displaystyle\lim_{n\to \infty}\displaystyle\frac{\textstyle\frac{1}{\tan x}-\textstyle\frac{1}{\tan^{n+2}x }+\textstyle\frac{1}{\tan^{2n+2}x } }{1+\textstyle\frac{1}{\tan^2x }+\textstyle\frac{1}{\tan^{2n+2}x}}\\[3pt]
=\displaystyle\frac{\textstyle\frac{1}{\tan x}}{1+\textstyle\frac{1}{\tan^2x }}\\[3pt]
=\tan x \cos^2x \\[3pt]
=\displaystyle\frac{1}{2}\sin 2x \ }\)
(i)〜(iii)より
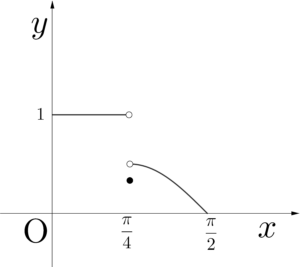
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
1\left(0\leqq x \lt \displaystyle\frac{\pi}{4}\right)\\
\displaystyle\frac{1}{3}\left(x=\displaystyle\frac{\pi}{4}\right)\\
\displaystyle\frac{1}{2}\sin 2x\left(\displaystyle\frac{\pi}{4}\lt x \lt \displaystyle\frac{\pi}{2}\right)
\end{array}
\right.
\end{eqnarray} \ }\)

この問題の\(\small{ \ y=f(x) \ }\)のグラフは図の形になるから、グラフを書くところまでマスターしよう。