確率漸化式のテクニック（前編）

こんにちは、リンス(@Lins016)です。
今回は確率漸化式のテクニックについて学習していこう。

確率漸化式の解き方

確率漸化式の基本については前回の記事で学習したけど、今回はもう少し難しい確率漸化式の問題を学習していこう。

記事の内容が長くなったから、前編と後編の二つの記事に分けたからどちらの記事も確認してほしい。

まずは確率漸化式を利用する問題では、確率漸化式を使う問題が見分ける必要があるよね。その辺りについては前の記事を確認しておこう。

CHECK

: 確率漸化式の基本
確率漸化式を利用する場合の見分け方や、その解き方について解説しています。
続きを見る

確率漸化式のテクニック

①与えられていない確率も文字で置いてみる。
②\(\small{ \ n \ }\)における確率の和が\(\small{ \ 1 \ }\)になることを利用する。
③対称性がある問題は対称性を利用する。

確率漸化式のテクニック

今回は確率漸化式の問題の解説をポイントをおさえながら考えていこう。
まずはこの問題を確認しよう。

問題

正四面体\(\small{ \ \mathrm{ABCD} \ }\)の頂点を移動する点\(\small{ \ \mathrm{P} \ }\)がある。点\(\small{ \ \mathrm{P} \ }\)は、\(\small{ \ 1 \ }\)秒ごとに、隣の\(\small{ \ 3 \ }\)頂点のいずれかに等しい確率\(\small{ \ \displaystyle\frac{a}{3} \ }\)で移るか、もとの頂点に確率\(\small{ \ 1-a \ }\)で留まる。初め頂点\(\small{ \ \mathrm{A} \ }\)にいた点\(\small{ \ \mathrm{P} \ }\)が、\(\small{ \ n \ }\)秒後に頂点\(\small{ \ \mathrm{A} \ }\)にいる確率を\(\small{ \ p_n \ }\)とする。ただし、\(\small{ \ 0\lt a\lt1 \ }\)とし、\(\small{ \ n \ }\)は自然数とする。
(1)数列\(\small{ \ \left\{p_n\right\} \ }\)の漸化式を求めよ。
(2)確率\(\small{ \ p_n \ }\)を求めよ。

確率漸化式の基本で学習した「\(\small{ \ 1 \ }\)秒ごとに変化して\(\small{ \ n \ }\)秒後にある状態になっている確率」の問題だから\(\small{ \ n+1 \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)にいる確率を\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)にいる確率を使って表すことができたらいいよね。

\(\small{ \ n+1 \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)にいるのは
「\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)にいて、\(\small{ \ n+1 \ }\)秒後も\(\small{ \ \mathrm{A} \ }\)いる」
「\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{B} \ }\)にいて、\(\small{ \ n+1 \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)いる」
「\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{C} \ }\)にいて、\(\small{ \ n+1 \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)いる」
「\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{D} \ }\)にいて、\(\small{ \ n+1 \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)いる」
\(\small{ \ 4 \ }\)つの場合で、これらは排反だよね。

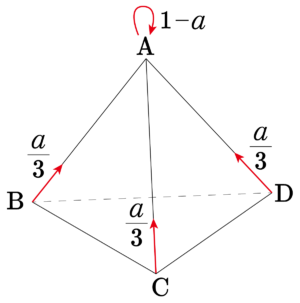
問題は\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)にいる確率だけ\(\small{ \ p_n \ }\)になっているけど、\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{B、C、D} \ }\)にいる確率をそれぞれ\(\small{ \ b_n,c_n,d_n \ }\)っておくと、漸化式は

\(\small{ \begin{eqnarray}
p_{n+1}&=&(1-a)p_n+\displaystyle\frac{a}{3}b_n+\displaystyle\frac{a}{3}c_n+\displaystyle\frac{a}{3}d_n\\
&=&(1-a)p_n+\displaystyle\frac{a}{3}(b_n+c_n+d_n)
\end{eqnarray} \ }\)

まずここが一つ目のポイントね。問題文には与えられていないけど、\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{B、C、D} \ }\)にいる確率もおいてみよう。そのほうが見通しがいい。

文字が多くなって複雑になった気がするけど、\(\small{ \ \mathrm{B、C、D} \ }\)は初めにいる\(\small{ \ \mathrm{A} \ }\)じゃない点ってことで、対称性があるよね。だから\(\small{ \ 2 \ }\)行目を見ると\(\small{ \ (b_n+c_n+d_n) \ }\)ってまとめられるからね。

次に大切なことが\(\small{ \ n \ }\)秒後の確率の和は\(\small{ \ 1 \ }\)になること。\(\small{ \ n \ }\)秒後は\(\small{ \ \mathrm{A、B、C、D} \ }\)のどこかにいるわけだから、\(\small{ \ p_n+b_n+c_n+d_n=1 \ }\)が成り立つよね。

だから、\(\small{ \ 2 \ }\)行目の\(\small{ \ b_n+c_n+d_n=1-p_n \ }\)になるんだ。これって、\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{A} \ }\)にいない確率だよね。

漸化式は

\(\small{ \begin{eqnarray}
p_{n+1}&=&(1-a)p_n+\displaystyle\frac{a}{3}(b_n+c_n+d_n)\\
&=&(1-a)p_n+\displaystyle\frac{a}{3}(1-p_n)
\end{eqnarray} \ }\)

になる。

結局、\(\small{ \ n \ }\)秒後に\(\small{ \ \mathrm{B、C、D} \ }\)にいる確率も文字でおいたけど、「対称性」や「n秒後の確率の和が1」を使うことでおいた文字を消すことができるんだ。

対称性がわかって、最初から\(\small{ \ \mathrm{B、C、D} \ }\)のいずれかにいる確率を\(\small{ \ 1-p_n \ }\)っておくことができる人は\(\small{ \ b_n,c_n,d_n \ }\)は使わなくてもいいけど、見通しが立たない人は問題文になくても自分で確率をおいて漸化式を立てるようにしよう。

漸化式が作れてしまえば、あとは漸化式を解くだけだからね。

問題の解答を確認

問題解答

\(\small{ \
\begin{eqnarray}
p_{n+1}&=&(1-a)p_n+\displaystyle\frac{a}{3}b_n+\displaystyle\frac{a}{3}c_n+\displaystyle\frac{a}{3}d_n\\
&=&(1-a)p_n+\displaystyle\frac{a}{3}(b_n+c_n+d_n)
\end{eqnarray} \ }\)

\(\small{ \ p_n+b_n+c_n+d_n=1 \ }\)であるから
\(\small{ \ p_{n+1}=(1-a)p_n+\displaystyle\frac{a}{3}(1-p_n) \ }\)
\(\small{ \ p_{n+1}=\left(1- \displaystyle\frac{4}{3}a\right)p_n+ \displaystyle\frac{a}{3} \ }\)

(2)(1)の漸化式を変形すると
\(\small{ \ p_{n+1}- \displaystyle\frac{1}{4}= \left(1- \displaystyle\frac{4}{3}a\right)\left(p_n- \displaystyle\frac{1}{4}\right) \ }\)
\(\small{ \ \mathrm{P} \ }\)ははじめ(\(\small{ \ 0 \ }\)秒のとき)、\(\small{ \ \mathrm{A} \ }\)にいるから\(\small{ \ p_0=1 \ }\)である。
よって\(\small{ \ \left\{p_n- \displaystyle\frac{1}{4}\right\} \ }\)は初項\(\small{ \ p_0- \displaystyle\frac{1}{4}= \displaystyle\frac{3}{4} \ }\)、公比\(\small{ \ 1- \displaystyle\frac{4}{3}a \ }\)の等比数列
\(\small{ \ p_n- \displaystyle\frac{1}{4}= \displaystyle\frac{3}{4}\left(1- \displaystyle\frac{4}{3}a\right)^n \ }\)
\(\small{ \ \therefore p_n= \displaystyle\frac{3}{4}\left(1- \displaystyle\frac{4}{3}a\right)^n+ \displaystyle\frac{1}{4} \ }\)

Point 確率漸化式のテクニック

①問題に与えられていない場合の確率も文字でおく。
②図形の対称性を考える。
③\(\small{ \ n \ }\)秒の確率の和が\(\small{ \ 1 \ }\)になることを利用する。

次は入試レベルの問題にチャレンジ！

入試レベルにチャレンジ

問題解答

最初\(\small{\mathrm{A}}\)、\(\small{\mathrm{B}}\)、\(\small{\mathrm{C}}\)の\(\small{ \ 3 \ }\)人が、\(\small{ \ \mathrm{A} \ }\)を先頭に\(\small{\mathrm{A}}\)、\(\small{\mathrm{B}}\)、\(\small{\mathrm{C}}\)の順で一列に並んでいる。さいころを投げるたびに、以下の操作を行う。
・\(\small{ \ 1 \ }\)の目が出たら、先頭の人と\(\small{ \ 2 \ }\)番目の人を入れ替える。
・\(\small{ \ 2 \ }\)の目が出たら、\(\small{ \ 2 \ }\)番目の人と\(\small{ \ 3 \ }\)番目の人を入れ替える。
・\(\small{ \ 1}\)、\(\small{ \ 2 \ }\)以外の目が出たら、入れ替えを行わない。
\(\small{ \ n \ }\)を自然数とする。\(\small{ \ n \ }\)回さいころを投げた後に\(\small{ \ \mathrm{A} \ }\)が先頭にいる確率を\(\small{ \ p_n \ }\)、\(\small{ \ \mathrm{A} \ }\)が\(\small{ \ 2 \ }\)番目にいる確率を\(\small{ \ q_n \ }\)とする。
(1)\(\small{ \ p_1}\)、\(\small{q_1 \ }\)を求めよ。
(2)\(\small{ \ p_{n+1}}\)、\(\small{ \ q_{n+1} \ }\)を\(\small{ \ p_{n}}\)、\(\small{ \ q_{n} \ }\)を用いてそれぞれ表せ。
(3)\(\small{ \ q_n \ }\)を求めよ。
(4) \(\small{ \ a_n=2^n\left(p_n-\displaystyle\frac{1}{3}\right) \ }\)とおき、\(\small{ \ a_{n+1} \ }\)と\(\small{ \ a_n \ }\)の関係式を求めよ。さらに、\(\small{ \ p_n \ }\)を求めよ。

(1)\(\small{ \ 1 \ }\)回のさいころを投げた後に\(\small{ \ \mathrm{A} \ }\)が先頭にいるのは、\(\small{ \ 1 \ }\)の目が出る以外だから
\(\small{ \ p_1=1-\displaystyle\frac{1}{6}=\displaystyle\frac{5}{6} \ }\)
\(\small{ \ 2 \ }\)番目にいるのは\(\small{ \ 1 \ }\)の目が出るときだから
\(\small{ \ q_1=\displaystyle\frac{1}{6} \ }\)

(2)\(\small{ \ n \ }\)回さいころを投げた後に\(\small{ \ \mathrm{A} \ }\)が\(\small{ \ 3 \ }\)番目にいる確率を\(\small{ \ r_n \ }\)とする。
順番が入れ替わる確率は次のようになる。

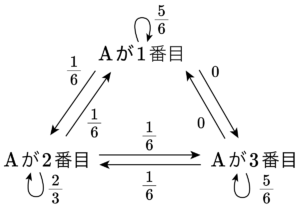
図より

\(\small{ \begin{aligned}
p_{n+1}&=\displaystyle\frac{5}{6}\times p_n+\displaystyle\frac{1}{6}\times q_n+0\times r_n\\
&=\displaystyle\frac{5}{6}p_n+\displaystyle\frac{1}{6}q_n
\end{aligned} \ }\)

同様に図から

\(\small{ \begin{aligned}
q_{n+1}&=\displaystyle\frac{1}{6}\times p_n+ \displaystyle\frac{2}{3}\times q_n+ \displaystyle\frac{1}{6} \times r_n\\
&=\displaystyle\frac{1}{6}p_n+\displaystyle\frac{2}{3}q_n+\displaystyle\frac{1}{6}r_n\\
&=\displaystyle\frac{1}{6}p_n+\displaystyle\frac{2}{3}q_n+\displaystyle\frac{1}{6}(1-p_n-q_n)\\
&=\displaystyle\frac{1}{2}p_n+ \displaystyle\frac{1}{6} \end{aligned} }\)

(3) \(\small{ \ q_{n+1}=\displaystyle\frac{1}{2}q_{n}+\displaystyle\frac{1}{6} \ }\)
これを変形して
\(\small{ \ q_{n+1}-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{2}\left(q_n-\displaystyle\frac{1}{3}\right) \ }\)
\(\small{ \ \left\{q_n-\displaystyle\frac{1}{3}\right\} \ }\)は初項\(\small{ \ q_1-\displaystyle\frac{1}{3}=-\displaystyle\frac{1}{6} \ }\)、公比\(\small{ \ \displaystyle\frac{1}{2} \ }\)の等比数列
\(\small{ \ q_n-\displaystyle\frac{1}{3}=-\displaystyle\frac{1}{6}\left(\displaystyle\frac{1}{2}\right)^{n-1} \ }\)
\(\small{ \begin{aligned}
q_n&=\displaystyle\frac{1}{3}-\displaystyle\frac{1}{6}\left(\displaystyle\frac{1}{2}\right)^{n-1}\\
&=\displaystyle\frac{1}{3}-\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{2}\right)^n \end{aligned} }\)

(4)\(\small{ \ p_{n+1}=\displaystyle\frac{5}{6}p_n+\displaystyle\frac{1}{6}q_n \ }\)
(3)より

\(\small{ \begin{aligned}
p_{n+1}&=\displaystyle\frac{5}{6}p_n+\displaystyle\frac{1}{6}\left\{\displaystyle\frac{1}{3}-\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{2}\right)^n\right\}\\
&=\displaystyle\frac{5}{6}p_n-\displaystyle\frac{1}{18}\left(\displaystyle\frac{1}{2}\right)^n+\displaystyle\frac{1}{18}
\end{aligned} }\)

両辺から\(\small{ \ \displaystyle\frac{1}{3} \ }\)ひくと

\(\small{ \begin{aligned}
p_{n+1}-\displaystyle\frac{1}{3}&=\displaystyle\frac{5}{6}p_n-\displaystyle\frac{1}{18}\left(\displaystyle\frac{1}{2}\right)^n-\displaystyle\frac{5}{18}\\
&=\displaystyle\frac{5}{6}\left(p_n-\displaystyle\frac{1}{3}\right)-\displaystyle\frac{1}{18}\left(\displaystyle\frac{1}{2}\right)^n
\end{aligned} \ }\)

両辺に\(\small{ \ 2^{n+1} \ }\)かけると

\(\small{ \ 2^{n+1}\left(p_{n+1}-\displaystyle\frac{1}{3}\right)=\displaystyle\frac{5}{3}\left(p_n-\displaystyle\frac{1}{3}\right)-\displaystyle\frac{1}{9} \ }\)

\(\small{ \ 2^n\left(a_n-\displaystyle\frac{1}{3}\right) \ }\)より
\(\small{ \ a_{n+1}=\displaystyle\frac{5}{3}p_n-\displaystyle\frac{1}{9} \ }\)
これを変形して
\(\small{ \ a_{n+1}-\displaystyle\frac{1}{6}=\displaystyle\frac{5}{3}\left(a_n-\displaystyle\frac{1}{6}\right) \ }\)
数列\(\small{ \ \left\{a_n-\displaystyle\frac{1}{6}\right\} \ }\)は初項\(\small{ \ a_1-\displaystyle\frac{1}{3}=2\left(p_1-\displaystyle\frac{1}{3}\right)-\displaystyle\frac{1}{6}=\displaystyle\frac{5}{6} \ }\)、公比\(\small{ \ \displaystyle\frac{5}{3} \ }\)の等比数列
\(\small{ \ a_{n}-\displaystyle\frac{1}{6}=\displaystyle\frac{5}{6}\left(\displaystyle\frac{5}{3}\right)^{n-1} \ }\)
\(\small{ \ a_n=\displaystyle\frac{1}{2}\left(\displaystyle\frac{5}{3}\right)^n+\displaystyle\frac{1}{6} \ }\)
\(\small{ \ 2^n\left(p_n-\displaystyle\frac{1}{3}\right)=\displaystyle\frac{1}{2}\left(\displaystyle\frac{5}{3}\right)^n+\displaystyle\frac{1}{6} \ }\)
\(\small{ \ p_n-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{5}{6}\right)^n+\displaystyle\frac{1}{6}\left(\displaystyle\frac{1}{2}\right)^n \ }\)
\(\small{ \ p_n=\displaystyle\frac{1}{2}\left(\displaystyle\frac{5}{6}\right)^n+\displaystyle\frac{1}{6}\left(\displaystyle\frac{1}{2}\right)^n+\displaystyle\frac{1}{3} \ }\)

確率漸化式は漸化式を立てられたら、あとは解くだけにしたい。だから漸化式は確実に全パターン解けるようにしておこう。この問題みたいに問題文が数列を与えていたら、その形に合わせて変形しよう。

確率漸化式の後編は下のリンクから！

CHECK

: 確率漸化式のテクニック（後編）
確率漸化式の解き方について、覚えておきたいテクニックについて解説しています。
続きを見る

確率漸化式のテクニック（前編）

確率漸化式の解き方

確率漸化式の基本

確率漸化式のテクニック

Point 確率漸化式のテクニック

確率漸化式のテクニック（後編）