こんにちは、リンス(@Lins016)です。
今回は確率漸化式について学習していこう。
確率漸化式とは
確率漸化式とはその名前の通り、確率の漸化式のこと。漸化式は数列の単元で、数列の一般項を求めるものだった。
確率漸化式はこれを確率に応用したもので、難関大学の入試によく出題されるイメージだったけど、最近では色々な大学でもわりと出題されてる。
「確率」+「漸化式」で難しく感じるけど、しっかりと理解できたら難しいことはないから、この記事を読んで、まずは確率漸化式の基本を理解しよう。
\(\small{ \ n \ }\)回目に状態\(\small{ \ \mathrm{A} \ }\)である確率を\(\small{ \ p_n \ }\)とすると
\(\small{ \ p_{n+1}=\alpha p_n + \beta(1-p_n) \ }\)
確率漸化式を使う問題の見分け方
もちろん問題に「確率漸化式を求めよ」なんて問題はない。定期試験等の易しい問題だったら小問(1)で「\(\small{ \ p_{n+1} \ }\)と\(\small{ \ p_n \ }\)の関係式を求めよ。」って問題から確率漸化式だって気づくかもしれないけど、入試ではなかなかそういう問題はない。
だから問題を読んで自分で漸化式を使うって判断しないといけない。じゃあ、どうやって判断するのかってなるんだけど、まずは『\(\small{ \ n \ }\)を含む確率の問題』を見たら確率漸化式を頭に浮かべていいと思う。
漸化式はある数列の\(\small{ \ n \ }\)番目と\(\small{ \ n+1 \ }\)番目の関係式(問題によっては\(\small{ \ n+2 \ }\)番目も)だから、問題に\(\small{ \ n \ }\)が出てくる必要があるよね。
だから\(\small{ \ n \ }\) を含む確率の問題では確率漸化式を考えてみることが大切なんだ。
実際よく出題されているのは次の\(\small{ \ 2 \ }\)つ。
①ある操作を繰り返して\(\small{ \ n \ }\)回目にある状態になっている確率
②\(\small{ \ 1 \ }\)秒ごとに変化して\(\small{ \ n \ }\)秒後にある状態になっている確率
もちろん、これ以外にも確率漸化式の問題はあるけど、上の形になっていることが多い。
ただ、注意しないといけないのが、\(\small{ \ n \ }\)を含む確率の問題には、確率漸化式を立てる問題以外にも、直接確率を求める問題もある。
例えば、「サイコロを\(\small{ \ 10 \ }\)回投げて\(\small{ \ n \ }\)回\(\small{ \ 3 \ }\)の倍数が出る確率を\(\small{ \ p_n \ }\)とする」のような問題もあるから、\(\small{ \ n \ }\)を含むから必ず確率漸化式になるってことはないんだけど、\(\small{ \ n \ }\)を含んで確率を直接求めることができなかったら、漸化式を立てられないかなって考えてほしい。
入試では\(\small{ \ n \ }\)を含む確率は色々な大学で出題されるから、確率漸化式以外の問題も記事にしていきたいと思っているけど、まずは確率漸化式から始めていく。

-

反復試行の確率
2つの事象の反復試行の確率や3つの事象の反復試行の確率について詳しく解説しています。
続きを見る
確率漸化式の解き方
それじゃ確率漸化式の具体的な解き方を見ていこう。
まずは具体例となる問題を見てみよう。
問題
\(\small{ \ n \ }\)個の袋の中に、それぞれ赤球が\(\small{ \ 1 \ }\)個、白球が\(\small{ \ 9 \ }\)個入っている。これら\(\small{ \ n \ }\)個の袋から、それぞれ\(\small{ \ 1 \ }\)個ずつ球を取り出したとき、赤球が奇数個取り出される確率を\(\small{ \ p_n \ }\)とする。\(\small{ \ p_n \ }\)を求めよ。
\(\small{ \ n \ }\)個の袋から、それぞれ\(\small{ \ 1 \ }\)個ずつ球を取り出すんだから、合計\(\small{ \ n \ }\)個球を取り出すことになる。このとき赤球が奇数個取り出される確率が\(\small{ \ p_n \ }\)だから、赤球が\(\small{ \ k \ }\)個だけ取り出される確率を\(\small{ \ q_k \ }\)とすると、求める確率は
\(\small{ \ p_n=q_1+q_3+q_5+q_7+ \cdots \ }\)ってなるよね。
これ直接求めるのは難しい。
確かに\(\small{ \ q_1 \ }\)は\(\small{ \ n \ }\)個の袋の中から\(\small{ \ 1 \ }\)袋は赤球、残りの\(\small{ \ n-1 \ }\)袋は白球を取り出す確率だから、
\(\small{ \ q_1={}_n\mathrm{C}_1\left(\displaystyle\frac{1}{10}\right)\left(\displaystyle\frac{9}{10}\right)^{n-1} \ }\)って求めることができる。
同様に考えれば、\(\small{ \ q_3={}_n \mathrm{C}_3\left(\displaystyle\frac{1}{10}\right)^3\left(\displaystyle\frac{9}{10}\right)^{n-3} \ }\)、\(\small{ \ q_5={}_n\mathrm{C}_1\left(\displaystyle\frac{1}{10}\right)^5\left(\displaystyle\frac{9}{10}\right)^{n-5} \ }\)、・・・って一つ一つ求めることはできるけど、これらを足すのは難しいし、\(\small{ \ n \ }\)が奇数か偶数かで、場合分けが必要になるよね。
つまり直接\(\small{ \ p_n \ }\)を求めるのは難しいから、確率漸化式を立ててみようって考えることから始まるんだ。
しかも、これはさっき話した①の「ある操作を繰り返して\(\small{ \ n \ }\)回目にある状態になっている確率」だよね。
\(\small{ \ n \ }\)回目にある状態になっている場合となっていない場合は排反であることに注意して漸化式を立てていこう。
確率漸化式は\(\small{ \ p_{n+1} \ }\)と\(\small{ \ p_n \ }\)の関係式(問題によっては\(\small{ \ p_{n+2} \ }\))を求めればいい。この問題では、\(\small{ \ n+1 \ }\)個の袋から赤球が奇数個取り出される確率\(\small{ \ p_{n+1} \ }\)と\(\small{ \ n \ }\)個の袋から赤球が奇数個取り出される確率\(\small{ \ p_{n} \ }\)の関係を求める。
\(\small{ \ n+1 \ }\)個の袋から赤球が奇数個取り出される(確率\(\small{ \ p_{n+1} \ }\))のは、
「\(\small{ \ n \ }\)個の袋から赤球が奇数個取り出されて(確率\(\small{ \ p_n \ }\))、次の袋から白球が取り出されるとき」と
「\(\small{ \ n \ }\)個の袋から赤球が偶数個取り出されて(確率\(\small{ \ 1-p_n \ }\))、次の袋から赤球が取り出されるとき」になる。(くどいけど、この2つは排反だからね。)
遷移図で表すと図のようになる。
確率漸化式では式を立てる前に一度遷移図書いてあげるとわかりやすい。簡単な遷移図を書いて問題を解くようにしよう。
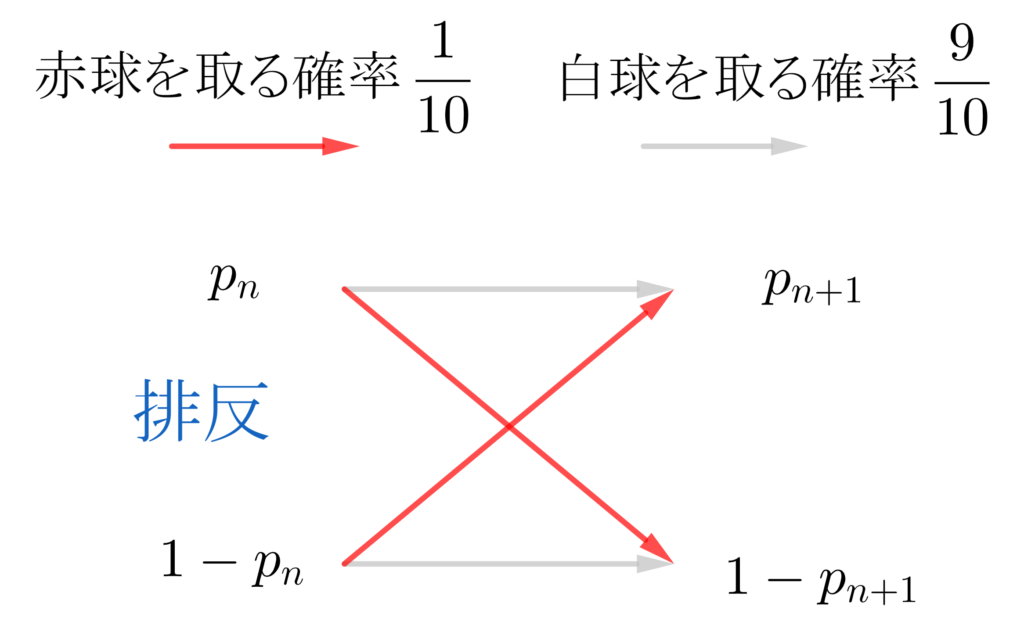
これを式にすると
\(\small{ \ p_{n+1}= \displaystyle\frac{9}{10}p_n+ \displaystyle\frac{1}{10}(1-p_n) \ }\)
\(\small{ \ \therefore p_{n+1}= \displaystyle\frac{4}{5}p_n+ \displaystyle\frac{1}{10} \ }\)
これで\(\small{ \ p_{n+1} \ }\)と\(\small{ \ p_n \ }\)の関係式が求まったよね。
あとは隣接二項間漸化式を解くことになるから、初項に注意して一般項求めればいい。
初項は自分で確率\(\small{ \ p_1 \ }\)を求める必要があるからね。
この漸化式を解く前に、漸化式を立てるところをもう一度確認しておこう。
\(\small{ \ n \ }\)個の袋から球を取った時点で、赤球の数は奇数個か偶数個だから、奇数個取る確率が\(\small{ \ p_n \ }\)なら、偶数個取る確率は\(\small{ \ 1-p_n \ }\)だよね。だって奇数個取るか偶数個取るかは排反だからね。ここが一番重要なところになるからね。
この問題の場合、\(\small{ \ n \ }\)個の袋から球を取り出して、その後\(\small{ \ n+1 \ }\)個目の袋から球を取り出すから、\(\small{ \ n+1 \ }\)個の袋から球を取り出したとき赤球を奇数個取るのは、\(\small{ \ n \ }\)個の袋から球を取り出したとき赤球が奇数個あるか偶数個あるかで次に取る球が変わってくるよね。
漸化式が作れたら、あとは漸化式を解けばいいよね。これは隣接二項間漸化式の特性方程式を利用する形だから、式を次のように等比数列の形に変形して答えを出そう。
\(\small{ \ p_{n+1}= \displaystyle\frac{4}{5}p_n+ \displaystyle\frac{1}{10}, \ p_1=\displaystyle\frac{1}{10} \ }\)
これを変形すると
\(\small{ \ p_{n+1}- \displaystyle\frac{1}{2}= \displaystyle\frac{4}{5}\left(p_n-\displaystyle\frac{1}{2}\right) \ }\)
\(\small{ \ \left\{p_n-\displaystyle\frac{1}{2}\right\} \ }\)は、初項\(\small{ \ p_1-\displaystyle\frac{1}{2}=-\displaystyle\frac{2}{5} \ }\)、公比\(\small{ \ \displaystyle\frac{4}{5} \ }\)の等比数列だから
\(\small{ \ p_n-\displaystyle\frac{1}{2}=-\dfrac{2}{5}\cdot \left(\displaystyle\frac{4}{5}\right)^{n-1} \ }\)
\(\small{ \ \therefore p_n=\displaystyle\frac{1}{2}-\dfrac{2}{5}\cdot \left(\displaystyle\frac{4}{5}\right)^{n-1} \ }\)
これが答えになるんだ。漸化式の解き方を忘れている人がいたら、漸化式の解き方を復習しておこう。
-

等比数列と特性方程式を利用する隣接二項間漸化式
特性方程式がなぜ成り立つのかなどの疑問について詳しく解説しています。
続きを見る
確率漸化式の立て方
上の問題を一般化して考えてみよう。
「ある操作を繰り返して\(\small{ \ n \ }\)回目に状態\(\small{ \ \mathrm{A} \ }\)になっている確率\(\small{ \ p_n \ }\)」を求めるとき、\(\small{ \ n \ }\)回目に状態\(\small{ \ \mathrm{A} \ }\)になっている場合となっていない場合は排反であることが重要なんだ。
\(\small{ \ n \ }\)回目に状態\(\small{ \ \mathrm{A} \ }\)になっている確率が\(\small{ \ p_n \ }\)のとき、状態\(\small{ \ \mathrm{A} \ }\)になっていない確率は\(\small{ \ 1-p_n \ }\)になるからね。
\(\small{ \ n \ }\)回目に状態\(\small{ \ \mathrm{A} \ }\)になっていて、\(\small{ \ n+1 \ }\)回目にある状態\(\small{ \ \mathrm{A} \ }\)になる場合と、\(\small{ \ n \ }\)回目に状態\(\small{ \ \overline{\mathrm{A}} \ }\)になっていて、\(\small{ \ n+1 \ }\)回目に状態\(\small{ \ \mathrm{A} \ }\)になる場合を考えればいい。この遷移図を書こう。
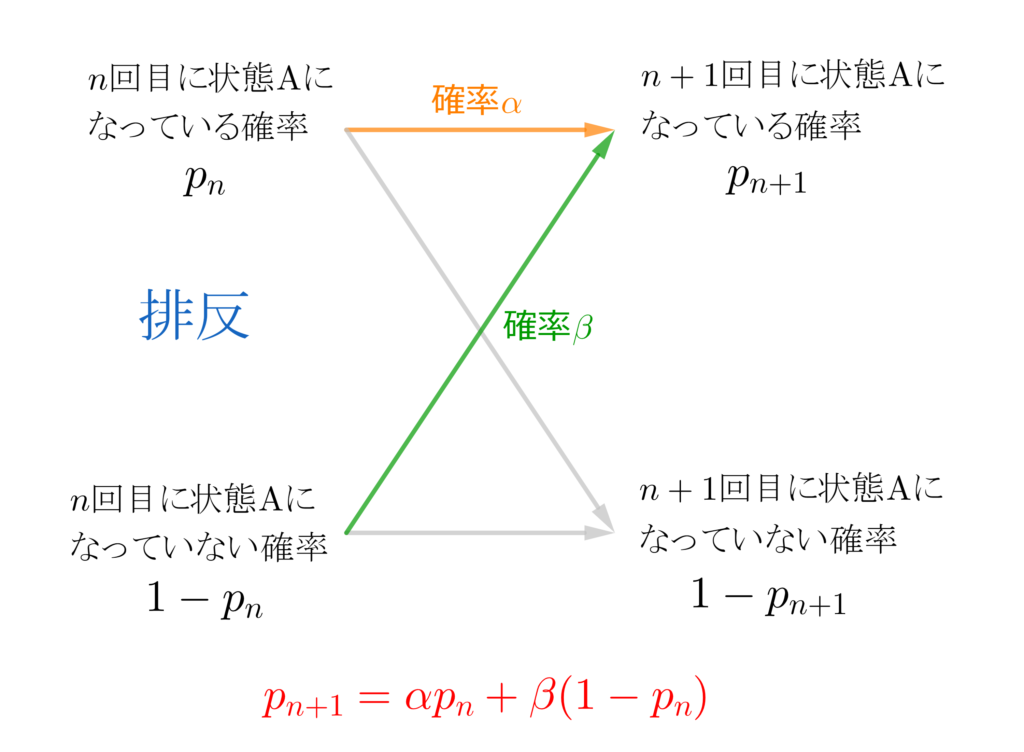
遷移図を書けば、遷移図の通り式を立てて、漸化式を解けばいいんだ。
Point 確率漸化式の基本
①\(\small{ \ n \ }\)を含む確率の問題で、直接確率を求めることができないときは漸化式を考えてみる。
②\(\small{ \ p_{n+1} \ }\)を\(\small{ \ p_n \ }\)と\(\small{ \ 1-p_n \ }\)の状態から考える。
③遷移図を書く。
\(\small{ \ 2 \ }\)つの粒子が時刻\(\small{ \ 0 \ }\)において、\(\small{ \ \triangle \mathrm{ABC} \ }\)の頂点\(\small{ \ \mathrm{A} \ }\)に位置している。これらの粒子は独立に運動し、それぞれ\(\small{ \ 1 \ }\)秒ごとに隣の頂点に等確率で移動していくとする。たとえば、ある時刻で点\(\small{ \ \mathrm{C} \ }\)にいる粒子は、その\(\small{ \ 1 \ }\)秒後には点\(\small{ \ \mathrm{A} \ }\)または点\(\small{ \ \mathrm{B} \ }\)にそれぞれ\(\small{ \ \displaystyle\frac{1}{2} \ }\)の確率で移動する。この\(\small{ \ 2 \ }\)つの粒子が、時刻\(\small{ \ 0 \ }\)の\(\small{ \ n \ }\)秒後に同じ点にいる確率\(\small{ \ p(n) \ }\)を求めよ。
\(\small{ \ n+1 \ }\)秒後に\(\small{ \ 2 \ }\)つの粒子が同じ位置にいるのは、
(i)\(\small{ \ n \ }\)秒後に同じ点にいて、その\(\small{ \ 1 \ }\)秒後に同じ点に移動する場合
(ii)\(\small{ \ n \ }\)秒後に異なる点にいて、その\(\small{ \ 1 \ }\)秒後に\(\small{ \ 2 \ }\)つの粒子がいなかった残りの点に移動する場合
の\(\small{ \ 2 \ }\)通りである。
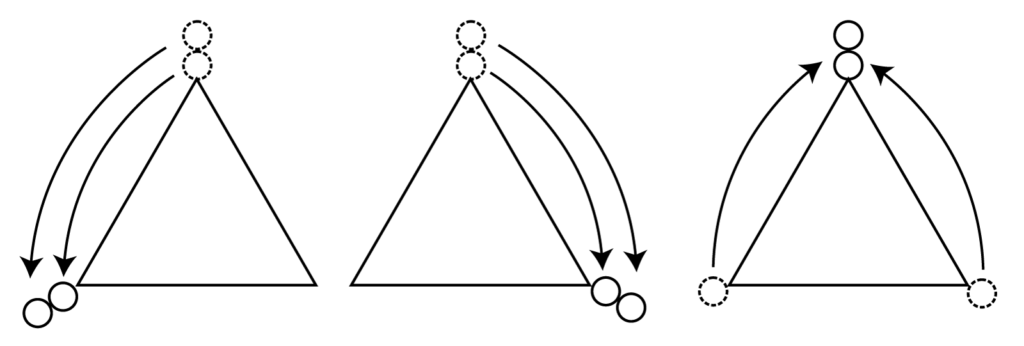
(i)\(\small{ \ n \ }\)秒後に同じ点にいて、その\(\small{ \ 1 \ }\)秒後に同じ点に移動する場合
\(\small{ \ p(n)\times\left(\displaystyle\frac{1}{2}\right)^2\times2=\displaystyle\frac{1}{2}p(n) \ }\)
(ii)\(\small{ \ n \ }\)秒後に異なる点にいて、その\(\small{ \ 1 \ }\)秒後に\(\small{ \ 2 \ }\)つの粒子がいなかった残りの点に移動する場合
\(\small{ \ \left(1-p(n)\right)\times\left(\displaystyle\frac{1}{2}\right)^2=\displaystyle\frac{1}{4}-\displaystyle\frac{1}{4}p(n) \ }\)
(i)(ii)は排反だから
\(\small{ \ p(n+1)=\displaystyle\frac{1}{2}p(n)+\displaystyle\frac{1}{4}-\displaystyle\frac{1}{4}p(n)\\
=\displaystyle\frac{1}{4}p(n)+ \displaystyle\frac{1}{4} \ }\)
これを変形すると
\(\small{ \ p(n+1)-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{4}\left\{p(n)-\displaystyle\frac{1}{3}\right\} \ }\)
\(\small{ \ p(0)=1 \ }\)より、\(\small{ \ \left\{p(n)-\displaystyle\frac{1}{3}\right\} \ }\)は初項\(\small{ \ \displaystyle\frac{2}{3} \ }\)、公比\(\small{ \ \displaystyle\frac{1}{4} \ }\)の等比数列であるから
\(\small{ \ p(n)-\displaystyle\frac{1}{3}=\displaystyle\frac{2}{3}\cdot\left(\displaystyle\frac{1}{4}\right)^n \ }\)
よって、\(\small{ \ p(n)=\displaystyle\frac{2}{3}\cdot\left(\displaystyle\frac{1}{4}\right)^n+\displaystyle\frac{1}{3} \ }\)



