確率漸化式のテクニック（後編）

こんにちは、リンス(@Lins016)です。
今回は確率漸化式のテクニックについて学習していこう。

目次[表示]

確率漸化式のテクニック

漸化式のテクニックは二つの記事に分けていて、前編を見てない人は、先に前編から見てほしい。

CHECK

: 確率漸化式のテクニック（前編）
確率漸化式の解き方について、覚えておきたいテクニックについて解説しています。
続きを見る

それと確率漸化式を使う問題か見分ける方法については下の記事を確認しておこう。

CHECK

: 確率漸化式の基本
確率漸化式を利用する場合の見分け方や、その解き方について解説しています。
続きを見る

確率漸化式のテクニック

①与えられていない確率も文字で置いてみる。
②対称性がある問題は対称性を利用する。
③ $\small{ \ n \ }$ における確率の和が $\small{ \ 1 \ }$ になることを利用する。
④問題によっては偶奇分けなど、ある数で割った余りで分類する。

確率漸化式のテクニック②

確率漸化式の問題でよく出題されるのが偶奇分けや $\small{ \ 3 \ }$ で割った余りで分類する問題。
次はそんな問題を確認していこう。

問題

図のように正三角形を $\small{ \ 9 \ }$ つの部屋に辺で区切り、部屋 $\small{ \ \mathrm{P、Q} \ }$ を定める。 $\small{ \ 1 \ }$ つの球が部屋 $\small{ \ \mathrm{P} \ }$ を出発し、 $\small{ \ 1 \ }$ 秒ごとに、そのまま部屋にとどまることなく、辺を共有する隣の部屋に等しい確率で移動する。球が $\small{ \ n \ }$ 秒後に部屋 $\small{ \ \mathrm{Q} \ }$ にある確率を求めよ。

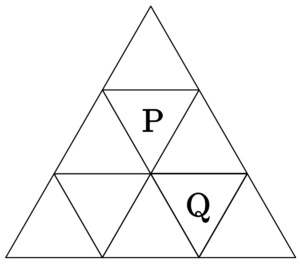
まず、この問題を見たときに図形の対称性を考えたい。図形の対称性を利用することで、 $\small{ \ 9 \ }$ つの部屋は次の $\small{ \ 3 \ }$ つのグループ（色）に分かれるんだ。

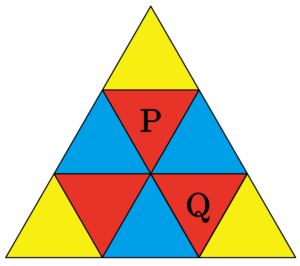
赤の部屋は $\small{ \ 3 \ }$ つの部屋と隣り合っているから、隣の部屋に移動する確率は $\small{ \ \displaystyle\frac{1}{3} \ }$ 。

青の部屋は $\small{ \ 2 \ }$ つの部屋と隣り合ってるから、隣の部屋に移動する確率は $\small{ \ \displaystyle\frac{1}{2} \ }$ 。

緑の部屋は $\small{ \ 1 \ }$ つの部屋と隣り合っているから、隣の部屋に移動する確率は $\small{ \ 1 \ }$ 。

この対称性は三角形を右に回転させて

$\small{ \ \mathrm{P} \ }$ が

$\small{ \ \mathrm{Q} \ }$ の位置にくるようしても図形は同じだから、対称が利用できるってことに気づいてほしい｡

下図のように各部屋に名前をつけて、 $\small{ \ n \ }$ 秒後にそれぞれの部屋にいる確率を部屋の名前の小文字で表しておこう。

$\small{ \ a_n、b_n、c_n、d_n、e_n、f_n、p_n、q_n、r_n \ }$

そして、 $\small{ \ n \ }$ 秒と $\small{ \ n+1 \ }$ 秒後の関係式を立てると次の関係式が成り立つよね。

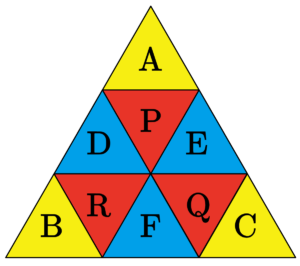
$\small{ \ a_{n+1}=\displaystyle\frac{1}{3}p_n\\[7pt] \ b_{n+1}=\displaystyle\frac{1}{3}r_n\\[7pt] \ c_{n+1}=\displaystyle\frac{1}{3}q_n\\[7pt] \ d_{n+1}=\displaystyle\frac{1}{3}p_n+\displaystyle\frac{1}{3}r_n\\[7pt] \ e_{n+1}=\displaystyle\frac{1}{3}p_n+\displaystyle\frac{1}{3}q_n\\[7pt] \ f_{n+1}=\displaystyle\frac{1}{3}q_n+\displaystyle\frac{1}{3}r_n\\[7pt] \ p_{n+1}=a_n+ \displaystyle\frac{1}{2}d_n+\displaystyle\frac{1}{2}e_n\\[7pt] \ q_{n+1}=c_n+ \displaystyle\frac{1}{2}e_n+\displaystyle\frac{1}{2}f_n \\[7pt] \ r_{n+1}=b_n+ \displaystyle\frac{1}{2}d_n+\displaystyle\frac{1}{2}f_n \ }$

文字がたくさんで大変だけど、求めたいのは $\small{ \ q_n \ }$ だから、まずはそれを頭に入れておこう。

つまり、 $\small{ \ q_n \ }$ と $\small{ \ q_{n+1} \ }$ の関係式を求めたいってことだからね。

$\small{ \ q_{n+1} \ }$ の式に他の式を代入すると

$\small{\begin{aligned} \ q_{n+1}&=c_n+\displaystyle\frac{1}{2}e_n+\dfrac{1}{2}f_n\\ &=\dfrac{1}{3}q_{n-1}+ \dfrac{1}{2}\left(\displaystyle\frac{1}{3}p_{n-1}+\displaystyle\frac{1}{3}q_{n-1} \right)+ \displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{3}q_{n-1}+ \displaystyle\frac{1}{3}r_{n-1}\right)\\ &=\displaystyle\frac{2}{3}q_{n-1} +\displaystyle\frac{1}{6}p_{n-1}+\displaystyle\frac{1}{6}r_{n-1}\end{aligned} \ }$

になる。この式を見ると何か気がつかないかな。

$\small{ \ n+1 \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいるのは $\small{ \ n−1 \ }$ 秒後に赤い部分にいるときだけなんだ。

当然 $\small{ \ n \ }$ 秒後に赤い部分にいて、 $\small{ \ n+1 \ }$ 秒後に赤い部分にいることは不可能だよね。

遅くともここでに気づかないといけない。最初 $\small{ \ \mathrm{P} \ }$ (赤い部分)から始まるから、奇数秒後は青か黄色の部分に、偶数秒後は赤い部分にいることになる。これは下の遷移図を見ても明らかだよね。

この矢印と数字は次に移動する確率を表しているんだけど、単純に部屋を色だけの区別にすると括弧内の確率になる。この問題では色だけの区別じゃ意味ないけど、問題によっては色だけの区別を利用することもあるから、問題によって遷移図を上のように書き換えたりしてあげよう。

このことから奇数秒後に $\small{ \ \mathrm{Q} \ }$ にいることはないから、偶数秒後だけ考えればいいんだ。

ここで、 $\small{ \ q_{n+1}=\displaystyle\frac{2}{3}q_{n-1} +\displaystyle\frac{1}{6}p_{n-1}+\displaystyle\frac{1}{6}r_{n-1} \ }$ を $\small{ \ q_{n+2}=\displaystyle\frac{2}{3}q_{n} +\displaystyle\frac{1}{6}p_{n}+\displaystyle\frac{1}{6}r_{n} \ }$ にしておこう。

意味としては同じだけど、一般に数列では $\small{ \ n \ }$ は自然数だから、 $\small{ \ n-1 \ }$ が出てきたら $\small{ \ n \geqq 2 \ }$ 以上って言わないといけなくなるよね。そうならないようにはじめから $\small{ \ n-1 \ }$ を使わないように設定しておきたい。

だからはじめから

$\small{\begin{aligned} \ q_{n+2}&=c_{n+1}+\displaystyle\frac{1}{2}e_{n+1}+\dfrac{1}{2}f_{n+1}\\ &=\dfrac{1}{3}q_{n}+ \dfrac{1}{2}\left(\displaystyle\frac{1}{3}p_n+\displaystyle\frac{1}{3}q_n \right)+ \displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{3}q_{n}+ \displaystyle\frac{1}{3}r_{n}\right)\\ &=\displaystyle\frac{2}{3}q_{n} +\displaystyle\frac{1}{6}p_{n}+\displaystyle\frac{1}{6}r_{n} \end{aligned} }$

って式にしたほうがいいね。

この問題は $\small{ \ 0 \ }$ 秒のとき $\small{ \ \mathrm{P} \ }$ にいるから $\small{ \ n=0 \ }$ も大丈夫だけど、結局 $\small{ \ n-1 \ }$ が出てきたら、 $\small{ \ n \geqq 1 \ }$ ってしないといけないからね。

そして、赤い部分にいるのは $\small{ \ n \ }$ は偶数のときだから $\small{ \ n=2m \ }$ として
$\small{ \ q_{2(m+1)}=\displaystyle\frac{2}{3}q_{2m} +\displaystyle\frac{1}{6}p_{2m}+\displaystyle\frac{1}{6}r_{2m} \ }$

また、偶数秒後は必ず赤い部分にいるから
$\small{ \ p_{2m}+q_{2m}+r_{2m}=1 \ }$

$\small{\begin{aligned} \ q_{2(m+1)}&=\displaystyle\frac{2}{3}q_{2m}+\displaystyle\frac{1}{6}(p_{2m}+r_{2m})\\ &=\displaystyle\frac{2}{3}q_{2m} +\displaystyle\frac{1}{6}(1-q_{2m})\\ &=\displaystyle\frac{1}{2}q_{2m}+\displaystyle\frac{1}{6} \end{aligned} }$

つまり、 $\small{ \ 2(m+1) \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ いるのは、 $\small{ \ 2m \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいて $\small{ \ 2(m+1) \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいる場合と $\small{ \ 2m \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ 以外にいて $\small{ \ 2(m+1) \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいる場合になるんだ。

これで $\small{ \ q_{2m} \ }$ の漸化式ができたよね。漸化式が作れてしまえば、あとは漸化式を解くだけだからね。それじゃ解答を確認しておこう。

問題の解答を確認

問題解答

図のように正三角形を $\small{ \ 9 \ }$ つの部屋に辺で区切り、部屋 $\small{ \ \mathrm{P,Q} \ }$ を定める。 $\small{ \ 1 \ }$ つの球が部屋 $\small{ \ \mathrm{P} \ }$ を出発し、 $\small{ \ 1 \ }$ 秒ごとに、そのまま部屋にとどまることなく、辺を共有する隣の部屋に等しい確率で移動する。球が $\small{ \ n \ }$ 秒後に部屋 $\small{ \ \mathrm{Q} \ }$ にある確率を求めよ。

部屋 $\small{ \ \mathrm{R} \ }$ を図のように定め、球が $\small{ \ n \ }$ 秒後に $\small{ \ \mathrm{P} \ }$ 、 $\small{ \ \mathrm{Q} \ }$ 、 $\small{ \ \mathrm{R} \ }$ にいる確率をそれぞれ、 $\small{ \ p_n \ }$ 、 $\small{ \ q_n \ }$ 、 $\small{ \ r_n \ }$ とする。
球ははじめ $\small{ \ \mathrm{P} \ }$ にあり、 $\small{ \ 1 \ }$ 秒毎に隣の部屋に移動することから、奇数秒後は $\small{ \ \mathrm{P} \ }$ 、 $\small{ \ \mathrm{Q} \ }$ 、 $\small{ \ \mathrm{R} \ }$ 以外の部屋に移動し、偶数秒後に $\small{ \ \mathrm{P} \ }$ 、 $\small{ \ \mathrm{Q} \ }$ 、 $\small{ \ \mathrm{R} \ }$ に移動する。

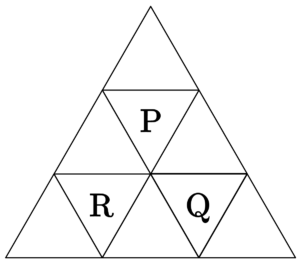
よって、 $\small{ \ m \ }$ を $\small{ \ 0 \ }$ 以上の整数とすると
$\small{ \ p_{2m+1}+q_{2m+1}+r_{2m+1}=0 \ }$
$\small{ \ p_{2m}+q_{2m}+r_{2m}=1 \ }$
$\small{ \ 2(m+1) \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいるのは
①「 $\small{ \ 2m \ }$ 秒後に $\small{ \ \mathrm{P} \ }$ にいて $\small{ \ 2(m+1) \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいる」
②「 $\small{ \ 2m \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいて $\small{ \ 2(m+1) \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいる」
③「 $\small{ \ 2m \ }$ 秒後に $\small{ \ \mathrm{R} \ }$ にいて $\small{ \ 2(m+1) \ }$ 秒後に $\small{ \ \mathrm{Q} \ }$ にいる」
場合である。
①の場合　 $\small{ \ \displaystyle\frac{1}{3}\times\displaystyle\frac{1}{2}=\displaystyle\frac{1}{6} \ }$
②の場合　 $\small{ \ \displaystyle\frac{1}{3}\times\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}\times1+ \displaystyle\frac{1}{3} \times \displaystyle\frac{1}{2}=\displaystyle\frac{2}{3} \ }$
③の場合　 $\small{ \ \displaystyle\frac{1}{3}\times\displaystyle\frac{1}{2}=\displaystyle\frac{1}{6} \ }$
よって
$\small{\begin{aligned} \ q_{2(m+1)}&= \displaystyle\frac{1}{6}q_{2m}+\displaystyle\frac{2}{3}q_{2m}+\displaystyle\frac{1}{6}r_{2m}\\ &=\displaystyle\frac{2}{3}q_{2m}+\displaystyle\frac{1}{6}(p_{2m}+r_{2m})\\ &=\displaystyle\frac{2}{3}q_{2m}+\displaystyle\frac{1}{6}(1-q_{2m})\\ &=\displaystyle\frac{1}{2}q_{2m}+\displaystyle\frac{1}{6} \end{aligned} }$
これを変形して
$\small{ \ q_{2m}-\displaystyle\frac{1}{3}= \displaystyle\frac{1}{2}(q_{2m}-\displaystyle\frac{1}{3}) \ }$
$\small{ \ \left\{q_{2m}-\dfrac{1}{3}\right\} \ }$ は、初項 $\small{ \ q_0-\displaystyle\frac{1}{3}=-\displaystyle\frac{1}{3} \ }$ 、公比 $\small{ \ \displaystyle\frac{1}{2} \ }$ の等比数列だから
$\small{ \ q_{2m}-\displaystyle\frac{1}{3}=-\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{2}\right)^m \ }$
$\small{ \ \therefore q_{2m}=\displaystyle\frac{1}{3}-\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{2}\right)^m \ }$
$\small{ \ n=2m \ }$ より
$\small{ \ n \ }$ が奇数のとき $\small{ \ q_n=0 \ }$
$\small{ \ n \ }$ が偶数のとき $\small{ \ q_n=\displaystyle\frac{1}{3}-\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{2}\right)^{\tiny{\displaystyle\frac{n}{2}}} \ }$

はじめ

$\small{ \ \mathrm{P} \ }$ に球があることと、図形的に

$\small{ \ \mathrm{Q} \ }$ と

$\small{ \ \mathrm{R} \ }$ は対称だから、

$\small{ \ n \ }$ 秒後に

$\small{ \ \mathrm{Q} \ }$ にいる確率

$\small{ \ q_n \ }$ と

$\small{ \ n \ }$ 秒後に

$\small{ \ \mathrm{R} \ }$ にいる確率

$\small{ \ r_n \ }$ は同じになるのもわかるよね。

つまり $\small{ \ r_n=\displaystyle\frac{1}{3}-\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{2}\right)^{\tiny{\displaystyle\frac{n}{2}}} \ }$
$\small{ \ p_n+q_n+r_n=1 \ }$ から
$\small{\begin{aligned} \ p_n&=1-q_n-r_n\\ &=\displaystyle\frac{1}{3}-\displaystyle\frac{2}{3}\left(\displaystyle\frac{1}{2}\right)^{\tiny{\displaystyle\frac{n}{2}}} \end{aligned} }$

さらに極限の考え方になるけど、 $\small{ \ n \ }$ を限りなく大きくすると
$\small{ \ \displaystyle\lim_{n\to \infty}p_n=\displaystyle\frac{1}{3} \ }$
$\small{ \ \displaystyle\lim_{n\to \infty}q_n=\displaystyle\frac{1}{3} \ }$
$\small{ \ \displaystyle\lim_{n\to \infty}r_n=\displaystyle\frac{1}{3} \ }$
になって、 $\small{ \ \mathrm{P、Q、R} \ }$ にいる確率は同じになることもわかるよね。
はじめに $\small{ \ \mathrm{P} \ }$ にいるから $\small{ \ p_n \ }$ だけ少し式は違うけど、 $\small{ \ n \ }$ が大きくなると $\small{ \ \mathrm{P、Q、R} \ }$ にいる確率は変わらないってことなんだ。

Point 確率漸化式のテクニック

①問題に与えられていない場合の確率も文字でおく。
②図形の対称性を考える。
③ $\small{ \ n \ }$ 秒の確率の和が $\small{ \ 1 \ }$ になることを利用する。
④問題によっては偶奇分けなど、ある数で割った余りで分類する。

次は入試レベルの問題にチャレンジ！

入試レベルにチャレンジ

問題解答

立方体のある頂点にマウスがいて $\small{ \ 1 \ }$ 回ごとに頂点からの頂点へ辺に沿って移動する。頂点に立つごとに、どの方向に進むかは(今来た辺を含めて)等確率であるとする。
$\small{ \ n \ }$ 回目の移動で最初の頂点に戻っている確率を $\small{ \ p_n \ }$ とする。 $\small{ \ p_n \ }$ を求めよ。

立方体の頂点を $\small{ \ \mathrm{ABCDEFGH} \ }$ とし、最初マウスが $\small{ \ \mathrm{A} \ }$ にいるとする。

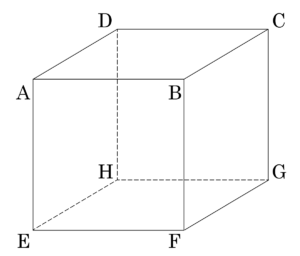
$\small{ \ 8 \ }$ 個の頂点を $\small{ \ A=\left\{\mathrm{A}\right\} \ }$ 、 $\small{ \ P=\left\{\mathrm{B,D,E}\right\} \ }$ 、 $\small{ \ Q=\left\{\mathrm{C,F,H}\right\} \ }$ 、 $\small{ \ R=\left\{\mathrm{G}\right\} \ }$ の組にわけると、遷移図は次のようになる。

このことからはじめの点 $\small{ \ \mathrm{A} \ }$ に戻るのは偶数回目の移動であることがわかる。よって $\small{ \ n \ }$ が奇数のとき $\small{ \ p_n=0 \ }$ である。
$\small{ \ n=2m \ }$ を考える。
$\small{ \ 2m \ }$ 回の移動でマウスは $\small{ \ A \ }$ の点か $\small{ \ Q \ }$ の点にいるから、 $\small{ \ 2(m+1) \ }$ 回の移動で $\small{ \ A \ }$ の点にいるのは、「 $\small{ \ 2m \ }$ 回の移動で $\small{ \ A \ }$ の点にいて $\small{ \ 2(m+1) \ }$ 回の移動で $\small{ \ A \ }$ にいる」場合と、「 $\small{ \ 2m \ }$ 回の移動で $\small{ \ A \ }$ の点にいて $\small{ \ 2(m+1) \ }$ 回の移動で $\small{ \ Q \ }$ にいる」場合である。 $\small{ \ n \ }$ 回の移動で $\small{ \ Q \ }$ の点にいる確率を $\small{ \ q_n \ }$ とすると、
$\small{ \ \begin{aligned} p_{2(m+1)}&=1\times\displaystyle\frac{1}{3}p_{2m} +\displaystyle\frac{2}{3}\times\displaystyle\frac{1}{3}q_{2m} \\ &=\displaystyle\frac{1}{3}p_{2m} +\displaystyle\frac{2}{9}q_{2m} \end{aligned} \ }$
偶数回では必ず $\small{ \ A \ }$ の点か $\small{ \ Q \ }$ の点にいるから、 $\small{ \ p_{2m}+q_{2m}=1 \ }$
$\small{ \ \begin{aligned} p_{2(m+1)}&=\displaystyle\frac{1}{3}p_{2m} +\displaystyle\frac{2}{9}(1-p_{2m})\\ &=\displaystyle\frac{1}{9}p_{2m}+\displaystyle\frac{2}{9} \end{aligned} \ }$
これを変形して
$\small{ \ p_{2(m+1)}-\displaystyle\frac{1}{4}=\displaystyle\frac{1}{9}\left(p_{2m}-\displaystyle\frac{1}{4}\right) \ }$
数列 $\small{ \ \left\{p_{2m}-\displaystyle\frac{1}{4}\right\} \ }$ は初項 $\small{ \ p_0-\displaystyle\frac{1}{4}=\displaystyle\frac{3}{4} \ }$ 、公比 $\small{ \ \displaystyle\frac{1}{9} \ }$ の等比数列
$\small{ \ p_{2m}-\displaystyle\frac{1}{4}=\displaystyle\frac{3}{4}\left(\displaystyle\frac{1}{9}\right)^{m} \ }$
$\small{ \ p_{2m}=\displaystyle\frac{3}{4}\left(\displaystyle\frac{1}{3}\right)^{2m}+\displaystyle\frac{1}{4} \ }$

よって求める確率は
$\small{ \ n \ }$ が奇数のとき　 $\small{ \ p_{n}=0 \ }$
$\small{ \ n \ }$ が偶数のとき　 $\small{ \ p_{n}=\displaystyle\frac{3}{4}\left(\displaystyle\frac{1}{3}\right)^{n}+\displaystyle\frac{1}{4} \ }$

$\small{ \ 8 \ }$ 個の頂点を

$\small{ \ S=\left\{\mathrm{A,C,F,H}\right\} \ }$ 、

$\small{ \ T=\left\{\mathrm{B,D,E,G}\right\} \ }$ の組にわけると、

$\small{ \ 1 \ }$ 回の移動で「

$\small{ \ S \ }$ から

$\small{ \ T \ }$ に移動する」か、「

$\small{ \ T \ }$ から

$\small{ \ S \ }$ に移動する」しかないこともわかるよね。

確率漸化式のテクニック（後編）

確率漸化式のテクニック

確率漸化式のテクニック（前編）

確率漸化式の基本

確率漸化式のテクニック②

Point 確率漸化式のテクニック