ベクトルを用いた三角形の面積の公式

こんにちは、リンス(@Lins016)です。
今回はベクトルを用いた三角形の面積の公式を学習していこう。

ベクトルを利用した三角形の面積の求め方

三角形の面積は、数学Iの図形と計量で三角比を使った面積の求め方を覚えたと思うけど、それを応用してベクトルでも三角形の面積を簡単に求められるように次の公式を覚えておこう。

この公式は空間ベクトルでも利用することができる、ホントに便利な式だからね。

三角形の面積

三角形の面積
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2} \ }\)

成分表示の場合
\(\small{ \ \overrightarrow{a}=(a_1, \ a_2), \ \overrightarrow{b}=(b_1, \ b_2) \ }\)とすると
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}|a_1b_2-a_2b_1| \ }\)

三角形の面積の公式

中学で教わった三角形の面積の公式というと底辺×高さ÷2だったよね。

高校数学では、数学Iの図形と計量で三角比を教わって、
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}ab\sin \mathrm{C} \ }\)だった。

実はこの式も底辺×高さ÷2の応用なんだけどね。この事については次の記事をチェックしておこう。

それじゃあ、この公式をベクトルにも応用させて考えていこう。

ベクトルを用いた三角形の面積

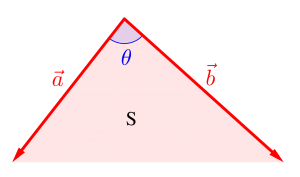
\(\small{ \ \triangle \mathrm{OAB} \ }\)の面積\(\small{ \ \mathrm{S} \ }\)は\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\mathrm{OA\cdot OB}\sin \angle \mathrm{AOB} \ }\)

これをベクトル表記にして
\(\small{ \ \mathrm{OA}=|\overrightarrow{a}| \ }\)、\(\small{ \ \mathrm{OB}=|\overrightarrow{b}| \ }\)、\(\small{ \ \angle \mathrm{AOB}=\theta \ }\)

\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|\sin\theta \\
&=&\displaystyle\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|\sqrt{1-\cos^2\theta}\\
&=&\displaystyle\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|\sqrt{1-\left(\displaystyle\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}\right)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2} \ \end{eqnarray}}\)

よって\(\small{ \ \triangle \mathrm{OAB} \ }\)の面積\(\small{ \ \mathrm{S} \ }\)はベクトルで表すと
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2} \ }\)
大文字表記で
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{\left|\overrightarrow{\mathrm{OA}}\right|^2\left|\overrightarrow{\mathrm{OB}}\right|^2-\left(\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}\right)^2} \ }\)
になる。

この式は空間ベクトルでも利用するから、しっかりと覚えておこう。

成分表示の三角形の面積

次に三角形の面積を成分表示で表してみよう。

\(\small{ \ \overrightarrow{a}=(a_1, \ a_2), \ \overrightarrow{b}=(b_1, \ b_2) \ }\)とすると

\(\small{ \ |\overrightarrow{a}|=\sqrt{a_1^2+a_2^2} \ }\)
\(\small{ \ |\overrightarrow{b}|=\sqrt{b_1^2+b_2^2} \ }\)
\(\small{ \ \overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2 \ }\)

上のベクトルを用いた三角形の面積にこの成分表示を代入すると

つまり\(\small{ \ \overrightarrow{a}=(a_1, \ a_2), \ \overrightarrow{b}=(b_1, \ b_2) \ }\)で作られる三角形の面積\(\small{ \ \mathrm{S} \ }\)は成分表示で
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}|a_1b_2-a_2b_1| \ }\)になる。

合わせて覚えておきたい面積の公式

成分表示の面積の式って実はベクトルを利用しなくても求めることができる。それは座標を利用した方法なんだ。

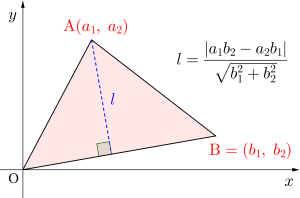
\(\small{ \ 3 \ }\)点\(\small{ \ (0, \ 0)、(a_1, \ a_2)、(b_1, \ b_2) \ }\)を頂点とする三角形の面積を\(\small{ \ \mathrm{S} \ }\)とすると、

\(\small{ \ (0, \ 0)、(b_1, \ b_2) \ }\)を通る直線の方程式は\(\small{ \ y=\displaystyle \frac{b_2}{b_1}x \ }\)

分母をはらって\(\small{ \ \therefore b_2x-b_1y=0 \ }\)
\(\small{ \ b_2x-b_1y=0 \ }\)と\(\small{ \ (a_1, \ a_2) \ }\)の距離\(\small{ \ l \ }\)は
\(\small{ \ l=\displaystyle \frac{|a_1b_2-a_2b_1|}{\sqrt{b_1^2+b_2^2}} \ }\)
よって求める三角形の面積\(\small{ \ \mathrm{S} \ }\)は
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle \frac{1}{2}\sqrt{b_1^2+b_2^2}\cdot l\\
&=&\displaystyle \frac{1}{2}|a_1b_2-a_2b_1| \ \end{eqnarray}}\)

この面積の求め方は数学IIの図形と方程式で教わる方法になるんだ。座標とベクトルの成分表示って同じように扱えるよね。

定期試験だと単元が決まってるけど、入試問題だとどの単元か分からないからベクトルで解くか座標として解くか迷ったりすることもあるから、どっちの方法も覚えておこう。