こんにちは、リンス(@Lins016)です。
今回は角の二等分線のベクトルについて学習していこう。
内分のベクトルと角の二等分線
三角形の角の二等分線と言われたら、二等分線の性質を必ず思い出そう。これに合わせて内分の公式を利用したらいいからね。
・内分を利用した角の二等分線
・単位ベクトルを利用した角の二等分線
\(\small{ \ \overrightarrow{\mathrm{OP}}=k\left(\displaystyle\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|}+\displaystyle\frac{\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OB}}|}\right) \ }\)
内分を利用した角の二等分線のベクトル
\(\small{ \ \triangle\mathrm{OAB} \ }\)の\(\small{ \ \angle \mathrm{AOB} \ }\)の角の二等分線について考えていこう。
\(\small{ \ \angle \mathrm{AOB} \ }\)の角の二等分線と線分\(\small{ \ \mathrm{AB} \ }\)の交点を\(\small{ \ \mathrm{P} \ }\)とすると、角の二等分線の性質から\(\small{ \ \mathrm{AP:PB=OA:OB} \ }\)になるよね。

ベクトルの内分の式を利用すると
だからこれを実数倍すれば直線を表すことになるから、任意の定数\(\small{ \ k \ }\)を利用して角の二等分線を表すことができるからね。
単位ベクトル
単位ベクトルとは「大きさが\(\small{ \ 1 \ }\)のベクトル」のこと。
だから\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と同じ向きの単位ベクトルは\(\small{ \ \displaystyle\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|} \ }\)って書くことができる。
\(\small{ \ |\overrightarrow{\mathrm{OA}}|=5 \ }\)なら\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と同じ向きの単位ベクトルは\(\small{ \ \displaystyle\frac{1}{5}\overrightarrow{\mathrm{OA}} \ }\)になるからね。
成分表示の場合\(\small{ \ \overrightarrow{\mathrm{OA}}=(3, \ 4) \ }\)なら\(\small{ \ |\overrightarrow{\mathrm{OA}}|=\sqrt{3^2+4^2}=5 \ }\)になるから同じ向きの単位ベクトルは\(\small{ \ \displaystyle\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|} \ }\)に代入して\(\small{ \ \left(\displaystyle\frac{3}{5}, \ \displaystyle\frac{4}{5}\right) \ }\)になるからね。
単位ベクトルと角の二等分線のベクトル
この単位ベクトルを利用して\(\small{ \ \angle\mathrm{OAB} \ }\)の角の二等分線を考えてみよう。
\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)と同じ向きの単位ベクトルは、それぞれ\(\small{ \ \displaystyle\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|} \ }\)と\(\small{ \ \displaystyle\frac{\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OB}}|} \ }\)になるよね。
\(\small{ \ \displaystyle\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|}+\displaystyle\frac{\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OB}}|} \ }\)は図のようになる。
\(\small{ \ \mathrm{OA'PB'} \ }\)はひし形になるから\(\small{ \ \mathrm{OP} \ }\)は\(\small{ \ \angle \mathrm{OA'B'}\ }\)を二等分するよね。
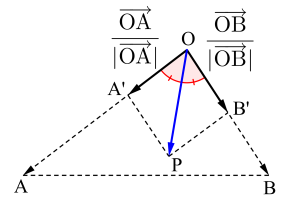
ってことは\(\small{ \ \displaystyle\frac{\overrightarrow{\mathrm{OA}}}{|\overrightarrow{\mathrm{OA}}|}+\displaystyle\frac{\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OB}}|} \ }\)の\(\small{ \ k \ }\)倍が角の二等分線になる。
ちなみに
=\displaystyle\frac{|\overrightarrow{\mathrm{OB}}|\overrightarrow{\mathrm{OA}}+|\overrightarrow{\mathrm{OA}}|\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|}\\
=\displaystyle\frac{|\overrightarrow{\mathrm{OA}}|+|\overrightarrow{\mathrm{OB}}|}{|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|}\left(\displaystyle\frac{|\overrightarrow{\mathrm{OB}}|}{|\overrightarrow{\mathrm{OA}}|+|\overrightarrow{\mathrm{OB}}|}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{|\overrightarrow{\mathrm{OA}}|}{|\overrightarrow{\mathrm{OA}}|+|\overrightarrow{\mathrm{OB}}|}\overrightarrow{\mathrm{OB}}\right) \ }\)
ってなるから内分の公式を利用した式の実数倍になっているのがわかるよね。
Point 角の二等分線のベクトル
①角の二等分線の性質を利用する
②単位ベクトルは大きさ\(\small{ \ 1 \ }\)のベクトル

