こんにちは、リンス(@Lins016)です。
今回は微分係数と導関数について学習していこう。
平均変化率と微分係数と導関数
関数\(\small{ \ y=f(x) \ }\)において\(\small{ \ \displaystyle \frac{f(b)-f(a)}{b-a} \ }\)を\(\small{ \ x \ }\)が\(\small{ \ a \ }\)から\(\small{ \ b \ }\)まで変化するときの平均変化率っていうから覚えておこう。
要するにある区間における変化の割合のことになるから、区間によって値は変わってくるからね。
この平均変化率の値は区間を定める二点の直線の傾きでもある。
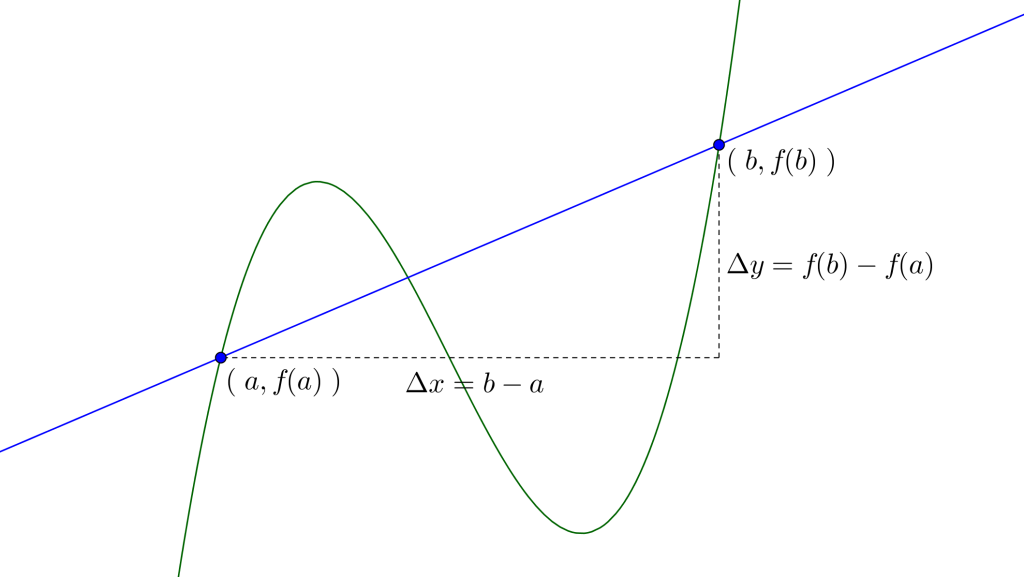
さらにこの\(\small{ \ b \ }\)を\(\small{ \ a+h \ }\)に書き換えて\(\small{ \ a \ }\)から\(\small{ \ a+h \ }\)までの平均変化率を考えてみよう。
\(\small{ \ h \ }\)が\(\small{ \ 0 \ }\)じゃない値から\(\small{ \ 0 \ }\)に限りなく近づくとき、この平均変化率の値の極限値を\(\small{ \ \displaystyle \lim_{ h \to 0 } \displaystyle \frac{f(a+h)-f(a)}{h}=f'(a) \ }\)で表して、この値を\(\small{ \ x=a \ }\)における微分係数っていうから覚えておこう。
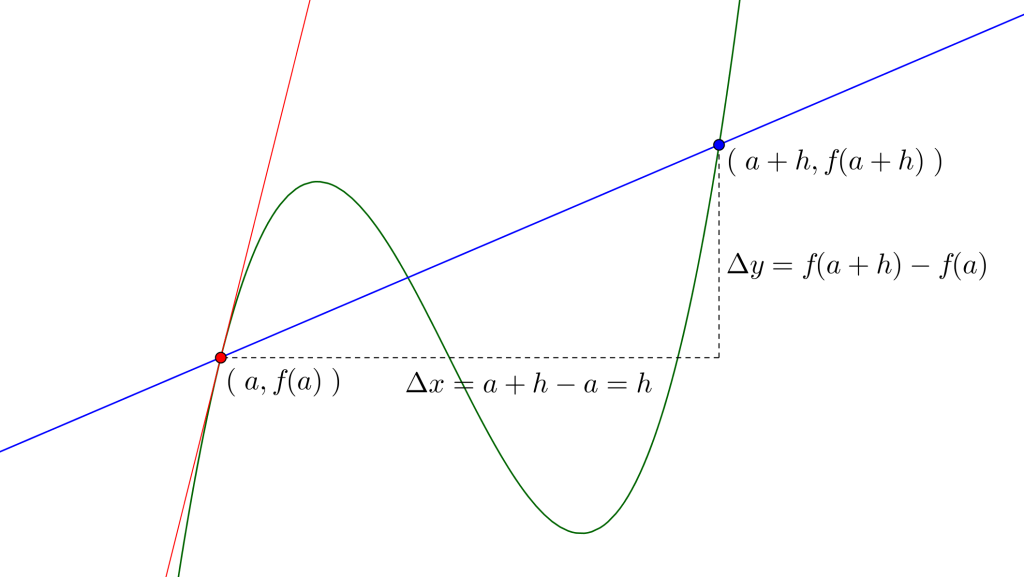
これは\(\small{ \ x=a \ }\)における\(\small{ \ y=f(x) \ }\)の接線の傾きになるんだ。
だって\(\small{ \ h \ }\)が\(\small{ \ 0 \ }\)に限りなく近付くってことは\(\small{ \ x=a \ }\)と\(\small{ \ x=a+h \ }\)が重なることになるから、この二点を結ぶ青い直線は、二点が\(\small{ \ x=a \ }\)で重なって図の赤い直線(接線)になる。
つまりこの微分係数の値を\(\small{ \ f'(a) \ }\)と記号で書き、\(\small{ \ y=f(x) \ }\)の\(\small{ \ x=a \ }\)における接線の傾きを表すから覚えておこう。
\(\small{ \ f'(a) \ }\)は\(\small{ \ x=a \ }\)における微分係数なんだけど、\(\small{ \ a \ }\)を\(\small{ \ f'(a) \ }\)に対応させて得られる関数を導関数っていって、\(\small{ \ f'(x) \ }\)って記号になる。
よく微分するっていうけど、それは\(\small{ \ f(x) \ }\)の導関数\(\small{ \ f'(x) \ }\)を求めることだからね。
また\(\small{ \ y \ }\)を微分したものを\(\small{ \ y’ \ }\)って書いたり、\(\small{ \ \displaystyle \frac{dy}{dx} \ }\)って書いたりするから覚えておこう。
・平均変化率(ある区間の変化の割合)
\(\small{ \ \displaystyle \frac{f(b)-f(a)}{b-a} \ }\)
・微分係数(ある点における接線の傾き)
\(\small{ \ f'(a)=\displaystyle \lim_{ h \to 0 } \displaystyle \frac{f(a+h)-f(a)}{h} \ }\)
・導関数(接線の傾きを示す関数)
\(\small{ \ f'(x)=\displaystyle \lim_{ h \to 0 } \displaystyle \frac{f(x+h)-f(x)}{h} \ }\)
定義に従って微分する
微分の定義とは\(\small{ \ f'(x)=\displaystyle \lim_{ h \to 0 } \displaystyle \frac{f(x+h)-f(x)}{h} \ }\)のことになるから、「定義に従って微分せよ」って問題では、この定義に代入して導関数を導かないといけない。
「定義に従って微分せよ」って問題は定期試験だけじゃなく入試でも出題されるから覚えておこう。
また、「定義に従って微分係数を求めよ」の場合は\(\small{ \ \displaystyle \lim_{ h \to 0 } \displaystyle \frac{f(a+h)-f(a)}{h}=f'(a) \ }\)になるから注意しよう。
公式を利用して微分する
毎回定義に従って微分するのはすごく大変だから「定義に従って微分せよ」って書いてない限り、公式を利用して微分しよう。
公式っていうのは「\(\small{ \ y=x^n \ }\)を微分すると\(\small{ \ y'=nx^{n-1} \ }\)になる」ことでこれを利用することで面倒な計算をしなくても簡単に微分係数を求めることができる。
複数の項が足された式はひとつひとつの項をそれぞれ微分して加えたらいいからね。
また、定数項は微分すると\(\small{ \ 0 \ }\)になるから覚えておこう。つまり\(\small{ \ y=2x^2-4x+3 \ }\)を微分すると\(\small{ \ y'=4x-4 \ }\)になる。簡単だよね。
(1)\(\small{ \ y=x^2 \ }\)の\(\small{ \ 1\leqq x \leqq 3 \ }\)における平均変化率を求めよ。
(2)次の極限値を求めよ。
\(\small{ \ \displaystyle \lim_{ x \to 3 } \displaystyle \frac{x^2-9}{x-3} \ }\)
(3)定義に従って\(\small{ \ f(x)=3x^2 \ }\)の\(\small{ \ x=2 \ }\)における微分係数を求めよ。
(4)公式を用いて\(\small{ \ f(x)=3x^2+2x-4 \ }\)の微分係数\(\small{ \ f'(1) \ }\)を求めよ。
(1)\(\small{ \ \displaystyle \frac{3^2-1^2}{3-1}=4 \ }\)
(2)\(\small{ \ \displaystyle \lim_{ x \to 3 } \displaystyle \frac{x^2-9}{x-3}= \displaystyle \lim_{ x \to 3 }(x+3)=6 \ }\)
(3)\(\small{ \ \displaystyle \lim_{ h \to 0 } \displaystyle \frac{3(2+h)^2-3\cdot2^2}{h} \ }\)
\(\small{ \ =\displaystyle \lim_{ h \to 0 } (12+3h)=12 \ }\)
(4)\(\small{ \ f(x)=3x^2+2x-4 \ }\)より\(\small{ \ f’(x)=6x+2 \ }\)
よって\(\small{ \ f'(1)=8 \ }\)

Point 微分係数と導関数
①微分係数\(\small{ \ f'(a) \ }\)は\(\small{ \ x=a \ }\)における接線の傾き
②導関数\(\small{ \ f'(x) \ }\)は接線の傾きを示す関数
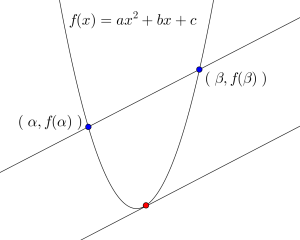
\(\small{ \ 2 \ }\)次関数\(\small{ \ f(x)=ax^2+bx+c \ }\)(ただし、\(\small{ \ a, \ b, \ c \ }\)は定数で、\(\small{ \ a \neq0 \ }\))において\(\small{ \ x=\alpha \ }\)から\(\small{ \ x=\beta \ }\)(\(\small{ \ \alpha \lt \beta \ }\))の平均変化率を求めよ。また、この平均変化率と微分係数が等しい\(\small{ \ x \ }\)の値を求めよ。
\(\small{\begin{eqnarray} \ &&\displaystyle \frac{f(\beta)-f(\alpha)}{\beta-\alpha}\\
&&=\displaystyle \frac{a(\beta^2-\alpha^2)+b(\beta- \alpha)}{\beta- \alpha}\\
&&=a(\alpha+\beta)+b \ \end{eqnarray}}\)
\(\small{ \ f(x)=ax^2+bx+c \ }\)より\(\small{ \ f'(x)=2ax+b \ }\)
\(\small{ \ 2ax+b=a(\alpha+\beta)+b \ }\)
\(\small{ \ x=\displaystyle \frac{\alpha+\beta}{2} \ }\)