分数関数の積分

こんにちは、リンス(@Lins016)です。
今回は分数関数の積分について学習していこう。

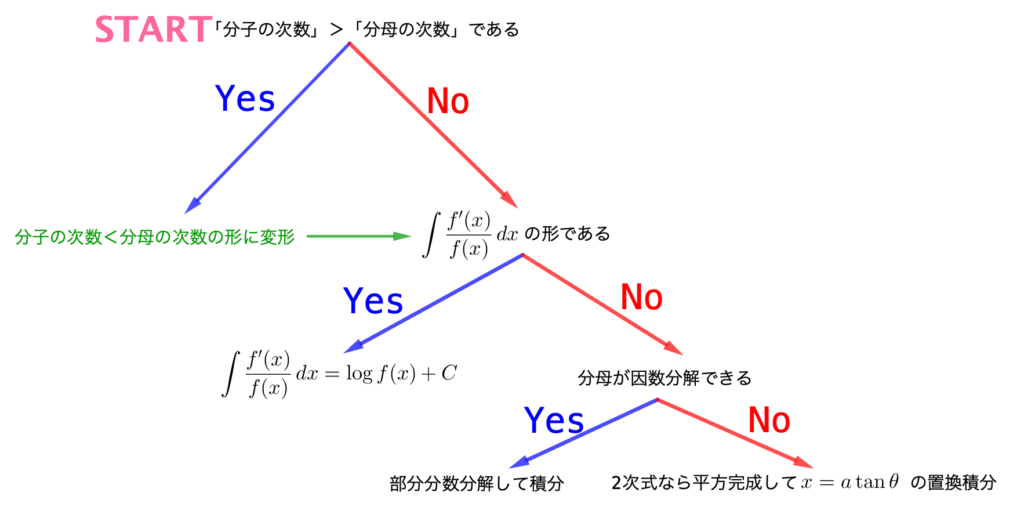
分数関数の積分の分類

分数の形をした関数の積分はいくつかパターンがある。特に分母分子がともに整式（\(\small{ \ n \ }\)次式の形）になっている関数で、分母分子の次数や形によって解き方が異なるから、今回はそのパターンについて考えていこう。

分母と分子の次数のチェック

積分する分数関数の分母と分子ともに整式の問題の場合、まずは分母と分子の次数を確認しよう。このとき分子の次数が分母の次数より大きい場合、分子を分母で割って分子の次数が分母の次数より小さくなるように変形しよう。

\(\small{ \ \displaystyle\frac{x^4+x^3+10}{x^3-3x+2}=x+1+\displaystyle\frac{3x^2+x+8}{x^3-3x+2} \ }\)

つまり

になるから前半の\(\small{ \ x+1 \ }\)の積分は簡単にできるから、\(\small{ \ \displaystyle\int \ \displaystyle\frac{3x^2+x+8}{x^3-3x+2} \ dx \ }\)を考えればいいことになる。

この分子の次数が分母の次数より小さいっていうのがとても重要になるから、分数関数の積分は常にこの形に変形しよう。

f'(x)/f(x)の確認

積分する分数関数の分子の次数が分母の次数より小さいとき、まずは\(\small{ \ \displaystyle\frac{f'(x)}{f(x)} \ }\)の形になってないか確認しよう。

\(\small{ \ \displaystyle\int \ \displaystyle\frac{f'(x)}{f(x)} \ dx=\log |f(x)|+C \ }\)になるんだったよね。

分数関数の積分は\(\small{ \ \displaystyle\int \ \displaystyle\frac{f'(x)}{f(x)} \ dx \ }\)の形になっていることが割と多い。

だからまずは分母と分子の次数を確認しよう。分母の次数より分子の次数が小さくないと、この形か確認できないから分子の次数を下げよう。

分子の次数が分母の次数より小さくなると、この形になってるか簡単に確認できるよね。

分数関数の積分は、分子の次数を下げて、分母の微分と分子を比較することから始めよう。違ったら他の解き方ってことになるからね。

分母が因数分解できる分数関数の積分

分母と分子がともに整式である分数関数の積分の場合、分母と分子の次数をチェックして、分子の次数を分母の次数より下げる。そして、\(\small{ \ \displaystyle\frac{f'(x)}{f(x)} \ }\)の形になっていないか確認する。

そして\(\small{ \ \displaystyle\frac{f'(x)}{f(x)} \ }\)の形になっていなかったとき、次にチェックするのが分母が因数分解できないかということ。

分母が因数分解できたら恒等式として部分分数分解してから積分の計算をしよう。部分分数分解がいまいちわからない人は次の例を確認して覚えよう。

例えば\(\small{ \ \displaystyle\int \ \displaystyle\frac{x+2}{x^2+x-6} \ dx \ }\)について考えてみよう。
分母の微分が分子になっていないよね。次に分母\(\small{ \ x^2+x-6 \ }\)が\(\small{ \ (x+3)(x-2) \ }\)と因数分解できるのに注目する。

だから\(\small{ \ \displaystyle\frac{x+2}{x^2+x-6} \ }\)なら\(\small{ \ \displaystyle\frac{x+2}{(x+3)(x-2)}= \displaystyle\frac{a}{x+3}+\displaystyle\frac{b}{x-2}\ }\)として\(\small{ \ a, \ b \ }\)を求めよう。

\(\small{\begin{eqnarray} \ \displaystyle\frac{x+2}{(x+3)(x-2)}&=&\displaystyle\frac{a}{x+3}+\displaystyle\frac{b}{x-2}\\[3pt] &=&\displaystyle\frac{a(x-2)+b(x+3）}{(x+3)(x-2)}\\
&=&\displaystyle\frac{(a+b)x-2a+3b}{(x+3)(x-2)} \ \end{eqnarray}}\)
これは\(\small{ \ x \ }\)についての恒等式だから係数を比較して
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
a+b&=&1 \\
-2a+3b&=&2
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=\displaystyle\frac{1}{5}, \ b=\displaystyle\frac{4}{5} \ }\)
\(\small{ \ \therefore \displaystyle\frac{x+2}{(x+3)(x-2)}= \displaystyle\frac{1}{5}\cdot\displaystyle\frac{1}{x+3}+\displaystyle\frac{4}{5}\cdot\displaystyle\frac{1}{x-2} \ }\)
になる。
この式変形が部分分数分解なんだ。

あとはこれを計算すればいいから
\(\small{ \begin{eqnarray}&&\displaystyle\int \ \displaystyle\frac{x+2}{(x+3)(x-2)} \ dx\\[3pt] &&=\displaystyle\int \ \left(\displaystyle\frac{1}{5}\cdot\displaystyle\frac{1}{x+3}+\displaystyle\frac{4}{5}\cdot\displaystyle\frac{1}{x-2}\right) \ dx\\[3pt] &&=\displaystyle\frac{1}{5}\log|x+3|+\displaystyle\frac{4}{5}\log |x-2|+C \ \end{eqnarray}}\)
（ただし\(\small{ \ C \ }\)は積分定数）
ってなるんだ。

それじゃ次に\(\small{ \ \displaystyle\int \ \displaystyle\frac{dx}{(x+1)(x+2)^2} \ dx \ }\)について考えてみよう。この場合も分母が因数分解できてるから、部分分数分解しよう。

とすると

これも\(\small{ \ x \ }\)についての恒等式だから係数を比較して
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
a+b=0 \\
4a+3b+c=0\\
4a+2b+c=1
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=1, \ b=-1, \ c=-1 \ }\)

（ただし\(\small{ \ C \ }\)は積分定数）
分母が因数分解できれば、部分分数分解して積分しよう。

この例みたいに分母が\(\small{ \ 3 \ }\)次式のとき、\(\small{ \ \displaystyle\frac{a}{(x+1)}+\displaystyle\frac{b}{(x+2)}+\displaystyle\frac{c}{(x+2)^2} \ }\)っておいたけど、『\(\small{ \ \displaystyle\frac{a}{(x+1)}+\displaystyle\frac{b}{(x+2)^2} \ }\)じゃダメなの？』って思わなかった？

これでも通分したら分母は\(\small{ \ (x+1)(x+2)^2 \ }\)になるよね。でもこれじゃダメなんだ。

もし\(\small{ \ 2 \ }\)つに分けるなら\(\small{ \ \displaystyle\frac{a}{(x+1)}+\displaystyle\frac{px+q}{(x+2)^2} \ }\)の形じゃないといけない。これじゃないと分子が\(\small{ \ 2 \ }\)次関数の\(\small{ \ \displaystyle\frac{lx^2+mx+n}{(x+1)(x+2)^2} \ }\)の形を全て表すことができないからね。

だから部分分数分解するとき、基本は分子の次数は分母の次数より\(\small{ \ 1 \ }\)次小さい式じゃないといけないんだ。
でもこの\(\small{ \ \displaystyle\frac{px+q}{(x+2)^2} \ }\)の形を積分するのってちょっと面倒。

だから\(\small{ \ \displaystyle\frac{px+q}{(x+2)^2} \ }\)の部分を\(\small{ \ \displaystyle\frac{b}{(x+2)}+\displaystyle\frac{c}{(x+2)^2} \ }\)ってしてるんだ。
こうすることで積分するとき簡単にできるからね。

ちなみに\(\small{ \ \displaystyle\int \ \displaystyle\frac{1}{(x+2)^2} \ dx \ }\)は置換積分で\(\small{ \ t=x+2 \ }\)とおいて\(\small{ \ \displaystyle\frac{dt}{dx}=1 \ }\)
\(\small{\begin{eqnarray}&&\displaystyle\int \ \displaystyle\frac{1}{(x+2)^2} \ dx\\[3pt] &&=\displaystyle\int \ t^{-2} \ dt\\[3pt] &&=\displaystyle\frac{1}{-2+1}t^{-2+1}+C\\[3pt] &&=-\displaystyle\frac{1}{x+2}+C\end{eqnarray}}\)
ってなるからね。

分母が2次式の因数分解できない関数の積分

最後に分母が\(\small{ \ 2 \ }\)次式の因数分解できない関数の積分について考えてみよう。この場合は因数分解できないから平方完成してみよう。
\(\small{ \ \displaystyle\int_2^3 \ \displaystyle\frac{1}{x^2-4x+5} \ dx=\displaystyle\int_2^3 \ \displaystyle\frac{1}{(x-2)^2+1} \ dx\ }\)
この分母が平方完成された形は無理やり\(\small{ \ a^2+x^2 \ }\)の\(\small{ \ x=a\tan \theta \ }\)って置換する置換積分に当てはめて計算しよう。
\(\small{ \ x-2=\tan \theta \ }\)とすると
\(\small{ \ \displaystyle\frac{dx}{d\theta}=\displaystyle\frac{1}{\cos^2\theta } \ }\)
\(\small{ \ \begin{array}{c|ccc}
x & 2 & \to & 3 \\
\hline
t & 0 & \to &\textstyle\frac{\pi}{4} \end{array} \ }\)
\(\small{\begin{eqnarray}&&\displaystyle\int_2^3 \ \displaystyle\frac{1}{x^2-4x+5} \ dx\\[3pt] &&=\displaystyle\int_2^3 \ \displaystyle\frac{1}{(x-2)^2+1} \ dx\\[3pt] &&=\displaystyle\int_{0}^{\textstyle\frac{\pi}{4}} \ \displaystyle\frac{1}{\tan^2\theta+1 }\cdot\displaystyle\frac{1}{\cos^2\theta }d\theta\\[3pt] &&=\displaystyle\int_{0}^{\textstyle\frac{\pi}{4}} \ d\theta\\[3pt] &&=\left[ \ \theta \ \right]_0^{\textstyle\frac{\pi}{4}}\\[3pt] &&=\displaystyle\frac{\pi}{4} \ \end{eqnarray}}\)

分母が\(\small{ \ 2 \ }\)次式\(\small{ \ ax^2+bx+c \ }\)の場合、\(\small{ \ ax^2+bx+c=0 \ }\)の判別式を\(\small{ \ D \ }\)とすると、\(\small{ \ D\gt0 \ }\)なら因数分解ができるから部分分数分解してから積分。

\(\small{ \ D=0 \ }\)なら分母が\(\small{ \ (ax+b)^2 \ }\)になるから置換積分。（実際置換するまでもないかもしれないけど、念の為）

\(\small{ \ D\lt0 \ }\)なら分母を平方完成して、\(\small{ \ a(x-p)^2+q \ }\)から\(\small{ \ \sqrt{q}\tan \theta=\sqrt{a}(x-p) \ }\)の置換積分。

どの形でも確実にできるようにしておこう。

Point 分数関数の積分

①分母と分子の次数をチェックする
②\(\small{ \ \displaystyle\int \ \displaystyle\frac{f'(x)}{f(x)} \ dx \ }\)の形か確認する
③分母が因数分解できたら部分分数分解
④分母が平方完成できたら置換積分