こんにちは、リンス(@Lins016)です。
今回は原因の確率について学習していこう。
原因の確率とは
原因の確率って言われる問題がある。これは条件付き確率の問題の中の1つなんだけど、条件付き確率の問題の中でも、比較的苦手としている人が多いと言われる問題なんだ。
教科書には原因の確率なんて書いてないけど、色々な問題集には取り上げられているから、今回の記事できちんと理解して解けるようにしよう。
・原因の確率
ある事象が起こったという結果から、この結果をもたらした原因がどの事象によるものであるかの確率
事象\(\small{ \ A \ }\)が起こった原因が事象\(\small{ \ B \ }\)である確率
\(\small{ \ P_A(B)=\displaystyle\frac{P(A\cap B)}{P(A)} \ }\)
・ベイズの定理(覚える必要なし!)
\(\small{ \ P_E(A_i)=\displaystyle\frac{P(A_i)P_{A_i}(E)}{\displaystyle\sum_{k=1}^{n}P(A_k)P_{A_k}(E)} \ }\)
原因の確率
原因の確率とは「ある事象が起こったという結果から、この結果をもたらした原因がどの事象によるものであるかの確率」のことで、これだけ聞くと「?」ってなるよね。
今回は次の問題で原因の確率を理解していこう。
問題を確認
同一の製品を作っている\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)、\(\small{ \ \mathrm{C} \ }\)、\(\small{ \ \mathrm{D} \ }\)の\(\small{ \ 4 \ }\)つの機械がある。\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)、\(\small{ \ \mathrm{C} \ }\)、\(\small{ \ \mathrm{D} \ }\)は全製品のそれぞれ\(\small{ \ 10 \ }\)%、\(\small{ \ 20 \ }\)%、\(\small{ \ 30 \ }\)%、\(\small{ \ 40 \ }\)%を生産し、\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)、\(\small{ \ \mathrm{C} \ }\)、\(\small{ \ \mathrm{D} \ }\)の製品の不良品の割合は、それぞれ\(\small{ \ a \ }\)%、\(\small{ \ b \ }\)%、\(\small{ \ c \ }\)%、\(\small{ \ d \ }\)%であるとする。いま、全製品の中から\(\small{ \ 1 \ }\)個の製品をとり出したとき、それが不良品であったという。この製品が\(\small{ \ \mathrm{A} \ }\)の機械から生産された確率を求めよ。
問題集で見たことあるような問題だよね。でもこの問題を苦手にしている生徒は割と多い。理解している人には大したことないかもしれないけど、どうしてこの問題が苦手なのか考えてみよう。
普通は「原因によって結果が生じる」って考えるけど、原因の確率は「結果がどの原因によるのか求める」つまり時間的順序が逆になっているところが理解しずらいところになるんだ。
上の問題なら、\(\small{ \ 1 \ }\)個取り出した製品が「\(\small{ \ \mathrm{A} \ }\)の機械で生産された不良品である」確率なら簡単に考えられる。
でも、取り出した製品が「不良品」で「\(\small{ \ \mathrm{A} \ }\)の機械で生産されたもの」と時間的順序が逆になっているところが難しく感じるところなんだ。
でも実際は時間的順序は気にしなくてもいい。
単に全事象を
\(\small{ \ \mathrm{A} \ }\)で生産された良品・不良品、
\(\small{ \ \mathrm{B} \ }\)で生産された良品・不良品、
\(\small{ \ \mathrm{C} \ }\)で生産された良品・不良品、
\(\small{ \ \mathrm{D} \ }\)で生産された良品・不良品の
\(\small{ \ 8 \ }\)つの排反に分かれた部分集合から、
\(\small{ \ \mathrm{A} \ }\)で生産された不良品、
\(\small{ \ \mathrm{B} \ }\)で生産された不良品、
\(\small{ \ \mathrm{C} \ }\)で生産された不良品、
\(\small{ \ \mathrm{D} \ }\)で生産された不良品の
\(\small{ \ 4 \ }\)つに分かれた部分集合に取り直せばいいんだ。
ある事象(不良品をとる)が起こったという結果が条件として与えられ、この結果をもたらした原因がどの事象によるものであるか(\(\small{ \ \mathrm{A} \ }\)の機械で作られた)の確率が原因の確率だからね。
「結果が条件」ってところが難しく感じる部分だけど、結果を書き出してしまえば、普通の条件付き確率と同じ。
だから、この問題を解くと次のようになる。
解答を確認
不良品である事象を\(\small{ \ E \ }\)、製品が機械\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)、\(\small{ \ \mathrm{C} \ }\)、\(\small{ \ \mathrm{D} \ }\)で生産されたという事象をそれぞれ\(\small{ \ A \ }\)、\(\small{ \ B \ }\)、\(\small{ \ C \ }\)、\(\small{ \ D \ }\)とすると不良品である確率\(\small{ \ P(E) \ }\)は
よって求める確率\(\small{ \ P_E(A) \ }\)は

ベイズの定理
上の原因の確率で利用した条件付き確率の式
が成り立つよね。
この式の分母は確率の乗法定理\(\small{ \ P(A)P_{A}(E)=P(A \cap E) \ }\)を使うと、
って書ける。
これを一般化すると、互いに排反する事象\(\small{ \ A_1、A_2、\cdots、A_n \ }\)のどれか\(\small{ \ 1 \ }\)つが必ず起こり、これを原因として事象\(\small{ \ E \ }\)が起こったとき、\(\small{ \ E \ }\)が起こった原因が\(\small{ \ A_i \ }\)である確率は
\(\small{ \ =\displaystyle\frac{P(A_i)P_{A_i}(E)}{\displaystyle\sum_{k=1}^{n}P(A_k)P_{A_k}(E)} \ }\)になる。
これをベイズの定理って言ったりもする。教科書には載ってないけど、網羅系参考書には掲載されている。原因の確率とあわせて掲載されていることが多い。
でもこの定理自体、特に覚える必要はないかな。だってこれって条件付き確率そのものの式だし、この定理知らないからといって解けない問題もないからね。
詳しく考え出すと、\(\small{ \ P_E(A_i) \ }\)は\(\small{ \ E \ }\)という結果が起こった条件のもとで、原因となる事象\(\small{ \ A_i \ }\)が起こる確率だから事後確率って言ったり、\(\small{ \ P(A_i) \ }\)を事象\(\small{ \ A_i \ }\)の事前確率って言ったりもする。でも、こんな言葉覚えなくても大丈夫。
ただ、ここで紹介したのは、問題集を自分で解いたときに出てきたら、覚えないといけないのかなって思わないでほしいってことを伝えたかっただけなんだ。特に覚えなくても困らないから安心してほしい。
原因の確率(条件に結果が与えられている条件付き確率)がきちんと解ければ問題ない。定理って書いてあると絶対覚えないとって思うかもしれないけど、覚えておかなくて大丈夫だからね。
\(\small{ \ 5 \ }\)回に\(\small{ \ 1 \ }\)回の割合で帽子を忘れるくせのある\(\small{ \ \mathrm{K} \ }\)君が、正月に\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)、\(\small{ \ \mathrm{C} \ }\)軒を順に年始回りをして家に帰ったとき、帽子を忘れてきたことに気がついた。\(\small{ \ 2 \ }\)軒目の家\(\small{ \ \mathrm{B} \ }\)に忘れてきた確率を求めよ。
帽子をどこにも忘れない確率は\(\small{ \ \left(\displaystyle\frac{4}{5}\right)^3 \ }\)
よって、どこかの家に帽子を忘れた確率は
\(\small{ \ 1-\left(\displaystyle\frac{4}{5}\right)^3=\displaystyle\frac{61}{125} \ }\)
家\(\small{ \ \mathrm{A} \ }\)で忘れず、家\(\small{ \ \mathrm{B} \ }\)で忘れた確率は \(\small{ \ \displaystyle\frac{4}{5}\times\displaystyle\frac{1}{5}=\displaystyle\frac{4}{25} \ }\)
よって、帽子を忘れたことに気づき、それが家\(\small{ \ \mathrm{B} \ }\)である確率は\(\small{ \ \displaystyle\frac{\displaystyle\frac{4}{25}}{\displaystyle\frac{61}{125}}=\displaystyle\frac{20}{61} \ }\)

Point 原因の確率
①時間的順序は気にしない。
②全事象を条件(与えられた結果)に取り直す。
ある病原菌の検査試薬は、その病原菌に感染している個体に対し誤って陰性反応を示す確率が\(\small{ \ \displaystyle\frac{3}{100} \ }\)であり、感染していない個体に対し誤って陽性反応を示す確率が \(\small{ \ \displaystyle\frac{3}{100} \ }\) である。ある集団にこの試薬で病原菌の検査を行い、全体の \(\small{ \ 4 \ }\) %が陽性反応を示したとき、次の問に答えよ。
(1)病原菌に感染している個体が陽性反応を示す確率を求めよ。
(2)この集団から\(\small{ \ 1 \ }\)つの個体を取り出すとき、その個体が病原菌に感染している確率を求めよ。
(3)この集団の中で陽性反応を示した個体が、実際は病原菌に感染していない確率を求めよ。
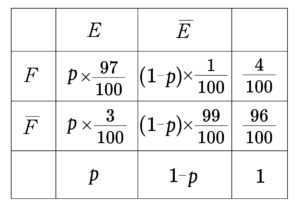
病原体に感染しているという事象を\(\small{ \ E \ }\)、陽性と判定されるという事象を \(\small{ \ F \ }\)とすると\(\small{ \ P(F)=\displaystyle\frac{4}{100} \ }\)、\(\small{ \ P(\overline{F})=\displaystyle\frac{96}{100} \ }\)、\(\small{ \ P_{E}(F)=\displaystyle\frac{97}{100} \ }\)
\(\small{ \ P_{E}(\overline{F})=\displaystyle\frac{3}{100} \ }\)、 \(\small{ \ P_{\overline{E}}(F)=\displaystyle\frac{1}{100} \ }\)、\(\small{ \ P_{\overline{E}}(\overline{F})=\displaystyle\frac{99}{100} \ }\)
(1)求める確率は\(\small{ \ P_{E}(F) \ }\)であるから,\(\small{ \ P_{E}(F)=\displaystyle\frac{97}{100} \ }\)
(2)求める確率は\(\small{ \ P(E) \ }\)である。
この確率を\(\small{ \ a \ (0\lt a\lt 1) \ }\)とすると、
\(\small{ \ P_{E}(F) \ }\)で
\(\small{\begin{eqnarray}P(F)&=&P(E \cap F)+P(\overline{E} \cap F)\\
&=&P(E) P_{E}(F)+P(\overline{E}) P_{\overline{E}}(F)\end{eqnarray}}\)
\(\small{ \ \displaystyle\frac{4}{100}=p \cdot \displaystyle\frac{97}{100}+(1-p) \cdot \frac{1}{100} \ }\)
\(\small{ \ 4=97 p+(1-p) \ }\)
\(\small{ \ p=\displaystyle\frac{1}{32} \ }\)
(3)陽性反応を示した個体が、実際は病原菌に感染していない条件付き確率は\(\small{ \ P_{\mathrm{F}}(\overline{E}) \ }\)であるから
\(\small{ \ P_{\mathrm{F}}(\overline{E})=\displaystyle\frac{P(F \cap E)}{P(F)}=\displaystyle\frac{\frac{1}{100} \cdot(1-p)}{\frac{4}{100}}=\displaystyle\frac{1-p}{4}=\displaystyle\frac{31}{128} \ }\)