こんにちは、リンス(@Lins016)です。
今回は平面ベクトルの基本について学習していこう。
ベクトルとは?ベクトルの考え方をマスターしよう
ベクトルとは大きさと向きを持つもので、高校数学では記号で書くと\(\small{ \ \vec{a} \ }\)や\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)、\(\small{ \ xy \ }\)平面での成分表示だと \(\small{ \ (a_1, \ a_2) \ }\)って書いたりする。
ベクトルの大きさは記号で\(\small{ \ | \vec{a}| \ }\)や \(\small{ \ | \overrightarrow{ \mathrm{OA} }| \ }\)で表す。成分表示だと \(\small{ \ \sqrt{{a_1}^2+{a_2}^2} \ }\)になる。
ベクトルは基準の二つのベクトルで表す
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)
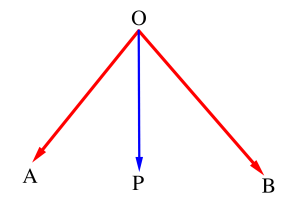
ベクトルの平行移動と実数倍
ベクトルは向きと大きさをもつものだけど、平行移動しても同じベクトルと見なすことができる。
つまりベクトルは位置によらず、どこにあっても向きと大きさが一緒なら等しいベクトルってことになるんだ。
さらにベクトル\(\small{ \ \vec{a} \ }\)を伸ばしたり、縮めたりするのは実数\(\small{ \ k \ }\)を利用して\(\small{ \ k\vec{a} \ }\)って書くことができる。
この平行移動と実数倍の考え方はベクトルを考える上で非常に大切だからしっかりと理解しておこう。
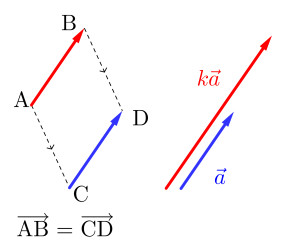
ベクトルの和はただ足し算するだけじゃダメ
ベクトルは向きと大きさを持つものだから、今までの数字のように足したり引いたりすることができない。
普段使っている数はプラスとマイナスの向きしかないから足したり引いたり簡単にできるけど、ベクトルの場合は単純な足し算ではなく、図を用いて足し算する必要がある。
ベクトルは平行移動して位置を変更しても同じベクトルだから、平行移動してベクトル(矢印)の根元と先を重ね合わせることで和を表すことができる。
つまり\(\small{ \ \overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AP}} \ }\)になる。
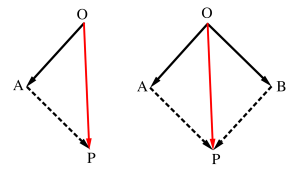
右の図の始点を揃えた二つのベクトルの和は、この二つのベクトルを各辺とする平行四辺形の対角線ってことになる。
平行移動したベクトルは等しいから\(\small{ \ \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{AP}} \ }\)で、これから\(\small{\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AP}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}} \ }\)になるよね。
ベクトルは始点を揃えよう
ベクトルを解く上で大事なことは「始点を揃える」こと。
始点って言うのはベクトルが始まる位置で、それに対してベクトルが終わる位置(矢印の先)を終点っていうからね。
\(\small{ \ \overrightarrow{ \mathrm{AB} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{BC} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)って始点がバラバラだよね。
こうなっているとベクトルは扱いにくいんだ。
っていうのもベクトルは向きと大きさを持つものだよね。
図のように点\(\small{ \ \mathrm{O} \ }\)から点\(\small{ \ \mathrm{A} \ }\)を見ると右向きだけど、点\(\small{ \ \mathrm{B} \ }\)から\(\small{ \ \mathrm{A} \ }\)を見ると左向きだよね。
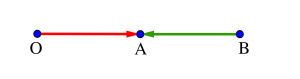
同じ点を見てるのに始点が違うと右向きだったり左向きだったりして向きが変わるし、さらに大きさも変わってくる。
だから始点がバラバラなベクトルはホント扱いにくい。
基準となる始点から見てどの向きにどれくらいの大きさって統一してあったほうが絶対わかりやすいから、常に始点を揃えることが大切になるんだ。
ベクトルは始点を揃えよう
始点の揃え方は\(\small{ \ \overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{ON}}-\overrightarrow{\mathrm{OM}} \ }\)のようにすることで始点を変更することができる。
ベクトルの和から\(\small{ \ \overrightarrow{\mathrm{ON}}=\overrightarrow{\mathrm{OM}}+ \overrightarrow{\mathrm{MN}} \ }\)がいえるから、これを移項することで\(\small{ \ \overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{ON}}-\overrightarrow{\mathrm{OM}} \ }\)が導けるよね。
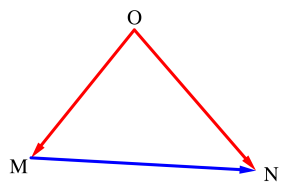
そろえたい始点の文字\(\small{ \ ■}\)(\(\small{■}\)はどんな文字でもOK)を文字の前に付けて、終点\(\small{ \ \mathrm{N} \ }\)のベクトルから始点の文字\(\small{ \ \mathrm{M} \ }\)のベクトルを引くことで始点を変更することが出来る。
\[\Large{ \ \overrightarrow{\mathrm{MN}}=\overrightarrow{■\mathrm{N}}-\overrightarrow{■\mathrm{M}} \ }\]
常にこの形で始点を変更することを覚えておこう。
平面ベクトルは基準のベクトルが二つ必要
平面ベクトルでは基準となるベクトルが二つ必要になる。
二つのベクトルを使うとすべてのベクトルを表すことができるんだ。
実数\(\small{ \ s, \ t \ }\)と基準となるベクトル\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)と\(\small{ \ \overrightarrow{ \mathrm{OB} } \ }\)を使うとあるベクトル\(\small{ \ \overrightarrow{ \mathrm{OP} } \ }\)は
\(\small{ \ \overrightarrow{ \mathrm{OP} }=s\overrightarrow{ \mathrm{OA} }+t\overrightarrow{ \mathrm{OB} } \ }\)
と表すことができる。
例えば図の\(\small{ \ \overrightarrow{\mathrm{OP}} \ }\)は
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&\overrightarrow{\mathrm{OR}}+\overrightarrow{\mathrm{RP}}\\
&=&\displaystyle\frac{2}{3}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{1}{3}\overrightarrow{\mathrm{OB}} \ \end{eqnarray}}\)
って書けるよね。
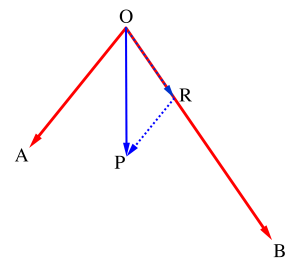
これは、点\(\small{ \ \mathrm{P} \ }\)から\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)に平行な直線を引いて、その直線と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)との交点を\(\small{ \ \mathrm{R} \ }\)ってすれば、あとは\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{RP}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OR}} \ }\)の長さの比を調べたら、\(\small{ \ \overrightarrow{\mathrm{OP}} \ }\)は\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)を使って表すことができる。
始点が\(\small{ \ \mathrm{O} \ }\)にない適当な位置にあるベクトル\(\small{ \ \overrightarrow{\mathrm{ MN} } \ }\)も、始点が\(\small{ \ \mathrm{O} \ }\)になるように平行移動して、あとはさっきと同じように点\(\small{ \ \mathrm{P} \ }\)から\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)に平行な直線を引いて、その直線と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)との交点を\(\small{ \ \mathrm{R} \ }\)ってして、長さの比を調べたら\(\small{ \ \overrightarrow{ \mathrm{OP} }=s\overrightarrow{ \mathrm{OA} }+t\overrightarrow{ \mathrm{OB} } \ }\)の形で表すことができるよね。
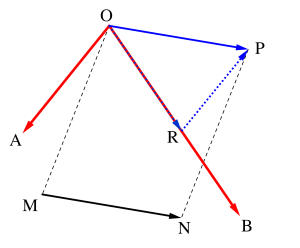
この図だと\(\small{ \ \overrightarrow{\mathrm{PR}} \ }\)は\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と逆向きだから\(\small{ \ s\lt0 \ }\)になる。
この場合長さを調べて、
\(\small{ \ \overrightarrow{\mathrm{MN}}=-\displaystyle\frac{2}{3}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{5}{9}\overrightarrow{\mathrm{OB}} \ }\)になる。
とにかく平面ベクトルでは二つの基準のベクトルでその他のベクトルを表すってことを心がけよう。

Point 平面ベクトルの基本
①ベクトルは始点を揃えよう
②平面ベクトルは二つの基準のベクトルでその他のベクトルを表そう

