こんにちは、リンス(@Lins016)です。
今回は放物線と円で囲まれる面積の求め方について学習していこう。
放物線と円で囲まれる面積の求め方
放物線と円で囲まれる面積には二つのパターンがあるんだ。
それは「放物線と円の2本の線で囲まれる面積」と「放物線と円と直線の3本の線で囲まれる面積」のパターン。
理系で数学Ⅲまで勉強した人は、円の面積を円の方程式を積分して求めることが出来るけど、放物線と円で囲まれる面積は数学Ⅱの範囲で出題されるから、円の方程式を積分する必要はないんだ。
だから今回学習する内容をしっかりと押さえておこう。
・放物線と円の2本の線で囲まれる面積
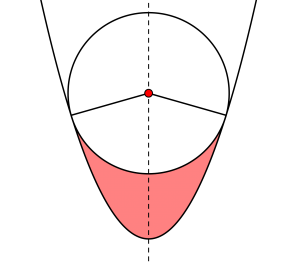
・放物線と円と直線の3本の線で囲まれる面積
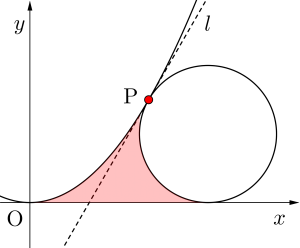
放物線と円の2本の線で囲まれる面積
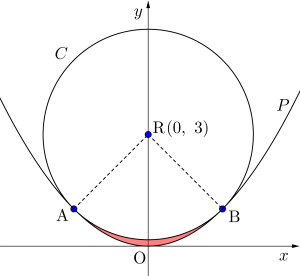
放物線と円の2本で囲まれる面積の場合、円の中心が放物線の軸上にある。まずはこのことを確認しておこう。
このとき放物線と円で囲まれる図の赤い部分の面積を求めることになるからね。

この面積を求める前に円と放物線の共有点について復習しておこう。
図の円と放物線が接している図形だけど、接していない問題でも同じ考え方だからね。
面積は、まず図のオレンジ色の部分を求めて、そこから扇形の面積を引いて放物線と円で囲まれた面積を求めよう。
このとき放物線の軸の上に円の中心があるから、放物線の軸に対して対称な図形になってるよね。
だから軸より右側の面積を求めてそれを二倍すればいいんだ。
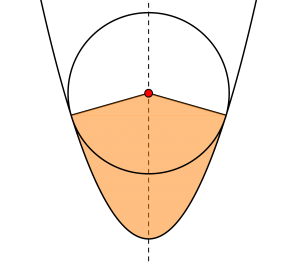
まずは円の中心や共有点の座標が必要になるからその値を求めよう。
次に円の中心と共有点を通る直線の方程式を求めよう。
この直線と放物線の差を円の中心の\(\small{ \ x \ }\)座標から共有点の\(\small{ \ x \ }\)座標で積分しよう。これが扇形を引く前の面積になるからね。
次に扇形の面積を求めよう。ここで重要なのが中心角\(\small{ \ \theta \ }\)なんだ。この中心角はさっき求めた円の中心と共有点を結ぶ直線の傾きから調べよう。
直線の傾きから\(\small{ \ x \ }\)軸となす角がわかるから、この中心角\(\small{ \ \theta \ }\)を求めることができるんだ。
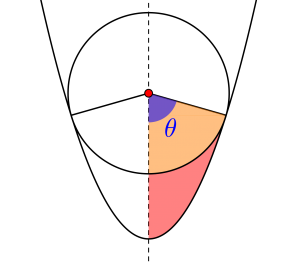
直線と\(\small{ \ x \ }\)軸とのなす角についてもう一度確認しておこう。
中心角が求まったら扇型の面積を求めて、さっき積分した面積から引いてあげよう。
あとは軸について対称だから、これを二倍すればOKだよね。
円\(\small{ \ C:x^2+(y-3)^2=a \ }\)と放物線\(\small{ \ P:y=\displaystyle\frac{1}{4}x^2 \ }\)について次の問いに答えよ。ただし、\(\small{ \ 0\lt a \lt 9 \ }\)とする。
(1)円\(\small{ \ C \ }\)と放物線\(\small{ \ P \ }\)の共有点が\(\small{ \ 2 \ }\)個のとき、\(\small{ \ a \ }\)の値を求めよ。
(2)(1)のとき共有点を\(\small{ \ \mathrm{A, \ B} \ }\)とするとき、線分\(\small{ \ \mathrm{AB} \ }\)の下側で円\(\small{ \ C \ }\)と放物線\(\small{ \ P \ }\)で囲まれる図形の面積を求めよ。
(1)円\(\small{ \ C:x^2+(y-3)^2=a \ }\)と放物線\(\small{ \ P:y=\displaystyle\frac{1}{4}x^2 \ }\)の式を連立すると
\(\small{ \ 4y+(y-3)^2=a \ }\)
\(\small{ \ \therefore y^2-2y+9-a=0\cdots① \ }\)
円\(\small{ \ C \ }\)と放物線\(\small{ \ P \ }\)の共有点が\(\small{ \ 2 \ }\)個のとき、
この\(\small{ \ y \ }\)の二次方程式は重解をもつので
\(\small{ ① }\)の判別式を\(\small{ \ D \ }\)とすると
\(\small{ \ D=(-2)^2-4(9-a)=0 \ }\)
\(\small{ \ \therefore a=8 \ }\)
(2)\(\small{ \ a=8 \ }\)を\(\small{①}\)に代入して
\(\small{ \ y=1 \ }\)よって\(\small{ \ x=\pm2 \ }\)
ここで円の中心と共有点を結ぶ直線の傾きは\(\small{ \ 1, \ -1 \ }\)より
軸と直線のなす角は\(\small{ \ \displaystyle\frac{\pi}{4} \ }\)
求める面積は放物線の軸に対称な図形より
&=&2\left\{\left[-\displaystyle\frac{1}{2}x^2+3x-\displaystyle\frac{1}{12}x^3\right]_{0}^{1}-\pi\right\}\\
&=&\displaystyle\frac{20}{3}-2\pi \ \end{eqnarray}}\)

放物線と円と直線の3本の線で囲まれる面積
今度は放物線と円が外接している図の面積を求めてみよう。
この面積は「放物線と円と\(\small{ \ x \ }\)軸(直線)で囲まれる面積」になるよね。
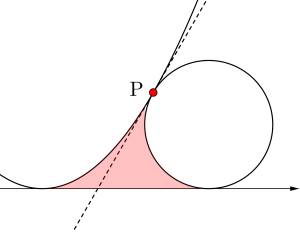
って言ってもいきなりこの面積を求めるのは難しいから、まずは次の図の面積を求めることを考えてみよう。

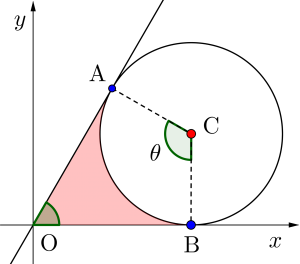
この斜めの直線は放物線と円の共通接線になるからね。さらに円は\(\small{ \ x \ }\)軸にも接しているから、\(\small{ \ \angle\mathrm{OAC}=\angle\mathrm{OBC}=\displaystyle\frac{\pi}{2} \ }\)になる。
面積は多角形\(\small{ \ \mathrm{OACB} \ }\)を求めて扇形を引けばいいんだけど、そのためには扇形の中心角\(\small{ \ \theta \ }\)を求める必要があるよね。
多角形\(\small{ \ \mathrm{OACB} \ }\)は\(\small{ \ \angle\mathrm{OAC}=\angle\mathrm{OBC}=\displaystyle\frac{\pi}{2} \ }\)だから\(\small{ \ \mathrm{OC} \ }\)を直径とする円周上に内接する四角形なんだ。
ってことは中心角\(\small{ \ \angle\mathrm{ACB}+\angle\mathrm{AOB}=\pi \ }\)になるから、斜めの直線と\(\small{ \ x\ }\)軸のなす角を求めて、扇形の中心角を求めよう。
中心角を求めたら多角形の面積から扇形の面積を引こう。
多角形の面積は点\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ x \ }\)軸に垂線を下ろし、三角形と台形に分けて面積を求めることができるからね。
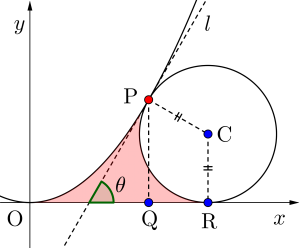
放物線\(\small{ \ C:y=\displaystyle\frac{\sqrt{3}}{4}x^2 \ }\)上の点\(\small{ \ \mathrm{P}\left(2, \ \sqrt{3}\right) \ }\)における接線を\(\small{ \ l \ }\)とする。第\(\small{ \ 1 \ }\)象限に中心を持つ円\(\small{ \ \mathrm{O} \ }\)が\(\small{ \ x \ }\)軸に接し、かつ直線\(\small{ \ l \ }\)に接するとき、次の問いに答えよ。
(1)点\(\small{ \ \mathrm{P} \ }\)を通り直線\(\small{ \ l \ }\)に直交する直線の方程式を求めよ。
(2)円\(\small{ \ \mathrm{O} \ }\)の中心の座標と半径を求めよ。
(3)円\(\small{ \ \mathrm{O} \ }\)の外部において、放物線\(\small{ \ C \ }\)、円\(\small{ \ \mathrm{O} \ }\)および\(\small{ \ x \ }\)軸によって囲まれた部分の面積を求めよ。
(1)\(\small{ \ y=\displaystyle\frac{\sqrt{3}}{4}x^2 \ }\)より\(\small{ \ y'=\displaystyle\frac{\sqrt{3}}{2}x \ }\)
点\(\small{ \ \mathrm{P} \ }\)における接線の傾きは\(\small{ \ \sqrt{3} \ }\)
これに垂直で点\(\small{ \ \mathrm{P} \ }\)を通る直線の方程式は
\(\small{\begin{eqnarray} \ y&=&-\displaystyle\frac{1}{\sqrt{3}}(x-2)+\sqrt{3}\\
&=&-\displaystyle\frac{1}{\sqrt{3}}x+\displaystyle\frac{5\sqrt{3}}{3} \ \end{eqnarray}}\)
(2)(1)で求めた直線上に円の中心はある
円の中心の座標は\(\small{ \ a \ }\)を用いて
\(\small{ \ \left(5-\sqrt{3}a, \ a\right) \ }\)とおける
また直線\(\small{ \ l \ }\)の方程式は
\(\small{\begin{eqnarray} \ y&=&\sqrt{3}(x-2)+\sqrt{3}\\
&=&\sqrt{3}x-\sqrt{3} \ \end{eqnarray}}\)
\(\small{ \ \therefore \sqrt{3}x-y-\sqrt{3}=0 \ }\)
この円が\(\small{ \ x \ }\)軸と\(\small{ \ l \ }\)の両方に接するので
\(\small{ \ \displaystyle\frac{|\sqrt{3}(5-\sqrt{3}a-a-\sqrt{3})}{\sqrt{(\sqrt{3})^2+(-1)^2}}=a \ }\)
\(\small{ \ |4\sqrt{3}-4a|=2a \ }\)
\(\small{ \ \therefore a=\displaystyle\frac{2\sqrt{3}}{3} \ }\)
中心の座標\(\small{ \ \left(3, \ \displaystyle\frac{2\sqrt{3}}{3}\right) \ }\)半径\(\small{ \ \displaystyle\frac{2\sqrt{3}}{3} \ }\)
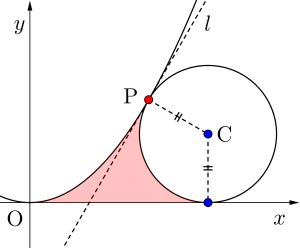
(3)\(\small{ \ \mathrm{R}(3, \ 0), \ \mathrm{Q}(2, \ 0) \ \mathrm{C}\left(3, \ \displaystyle\frac{2\sqrt{3}}{3}\right) \ }\)とおく
直線\(\small{ \ l \ }\)の傾きは\(\small{ \ \sqrt{3} \ }\)より
\(\small{ \ l \ }\)と\(\small{ \ x \ }\)軸のなす角\(\small{ \ \theta \ }\)は\(\small{ \ \theta=\displaystyle\frac{\pi}{3} \ }\)
これより\(\small{ \ \angle\mathrm{PCR}=\displaystyle\frac{2}{3}\pi \ }\)
よって求める面積は
\(\small{=\left[\displaystyle\frac{\sqrt{3}}{12}x^3\right]_{0}^{2}+\displaystyle\frac{1}{2}\left(\displaystyle\frac{2\sqrt{3}}{3}+ \sqrt{3}\right)\times 1-\displaystyle\frac{1}{2}\left(\displaystyle\frac{2\sqrt{3}}{3}\right)^2\cdot\displaystyle\frac{2}{3}\pi\\
=\displaystyle\frac{3\sqrt{3}}{2}-\displaystyle\frac{4}{9}\pi \ }\)

Point 放物線と円で囲まれる面積の求め方
①扇形をくり抜くようような面積から求める
②直線の傾きから扇形の中心角を求める
③扇形をくり抜く
曲線\(\small{ \ y=x^2 \ }\)を\(\small{ \ C_1 \ }\)とする。この\(\small{ \ C_1 \ }\)と\(\small{ \ x \ }\)軸の両方に接し、半径が\(\small{ \ \displaystyle\frac{1}{2} \ }\)の円を\(\small{ \ C_2 \ }\)とする。
(1)\(\small{ \ C_2 \ }\)の方程式を求めよ。
(2)\(\small{ \ C_2 \ }\)の外部において、\(\small{ \ C_1 \ }\)と\(\small{ \ C_2 \ }\)と\(\small{ \ x \ }\)軸で囲まれた部分の面積を求めよ。
(1)\(\small{ \ y=x^2 \ }\)より\(\small{ \ y'=2x \ }\)
接点の\(\small{ \ x \ }\)座標を\(\small{ \ t \ }\)とすると、
法線の方程式は
\(\small{\begin{eqnarray} \ y&=&-\displaystyle\frac{1}{2t}(x-t)+t^2\\
&=&-\displaystyle\frac{1}{2t}x+t^2+\displaystyle\frac{1}{2} \ \end{eqnarray}}\)
この法線上に円の中心はあるから、
円の中心の座標を\(\small{ \ \left(a, \ \displaystyle\frac{1}{2}\right) \ }\)とすると
\(\small{ \ \displaystyle\frac{1}{2}=-\displaystyle\frac{1}{2t}a+t^2+\displaystyle\frac{1}{2} \ }\)
\(\small{ \ \therefore a=2t^3 \ }\)
また円の方程式は
\(\small{ \ (x-a)^2+\left(y-\displaystyle\frac{1}{2}\right)=\displaystyle\frac{1}{4} \ }\)
これは接点\(\small{ \ (t, \ t^2) \ }\)も通るから
\(\small{ \ (t-a)^2+\left(t^2-\displaystyle\frac{1}{2}\right)=\displaystyle\frac{1}{4} \ }\)
これに\(\small{ \ a=2t^3 \ }\)を代入して
\(\small{ \ (t-2t^3)^2+\left(t^2-\displaystyle\frac{1}{2}\right)=\displaystyle\frac{1}{4} \ }\)
\(\small{ \ t^4(4t^2-3)=0 \ }\)
\(\small{ \ t\gt0 \ }\)より
\(\small{ \ t=\displaystyle\frac{\sqrt{3}}{2} \ }\)
\(\small{ \ a=2t^3=\displaystyle\frac{3\sqrt{3}}{4} \ }\)
\(\small{ \ \therefore \left(x-\displaystyle\frac{3\sqrt{3}}{4}\right)+\left(y-\displaystyle\frac{1}{2}\right)=\displaystyle\frac{1}{4} \ }\)
(2)法線の傾きは\(\small{ \ -\displaystyle\frac{1}{\sqrt{3}} \ }\)、
接線の傾きは\(\small{ \ \sqrt{3} \ }\)より,
扇形の中心角は\(\small{ \ \displaystyle\frac{2}{3}\pi \ }\)
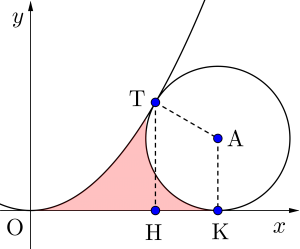
よって求める面積は
\(\small{=\displaystyle\int_{0}^{\scriptsize{\displaystyle\frac{\sqrt{3}}{2}}}x^2dx+\left(\displaystyle\frac{1}{2}+\displaystyle\frac{3}{4}\right)\left(\displaystyle\frac{3\sqrt{3}}{4}-\displaystyle\frac{\sqrt{3}}{2}\right)\cdot\displaystyle\frac{1}{2}-\pi\left(\displaystyle\frac{1}{2}\right)^2\cdot\displaystyle\frac{2/3\pi}{2\pi}\\
=\displaystyle\frac{9\sqrt{3}}{32}-\displaystyle\frac{\pi}{12} \ }\)

