こんにちは、リンス(@Lins016)です。
今回は放物線の基本について学習していこう。
二次曲線と放物線
放物線って言われたら、数学Iで学習した「二次関数」を思い浮かべると思うけど、二次関数で学習した放物線は軸が\(\small{ \ y \ }\)軸に平行な放物線だけを学習したよね。
でもこの二次曲線の単元では、軸が\(\small{ \ x \ }\)軸に平行な放物線も学習するんだ。
放物線って言うと物を斜めに投げたときの軌道をイメージすることが多いと思うけど、それ以外の性質を学習していこう。
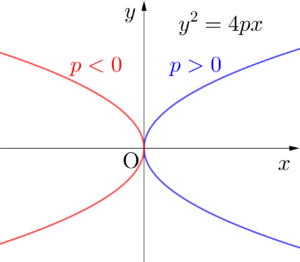
焦点\(\small{ \ (p,0) \ }\)、準線\(\small{ \ x=-p \ }\)のとき
\(\small{ \ y^2=4px \ }\)
焦点\(\small{ \ (0,p) \ }\)、準線\(\small{ \ y=-p \ }\)のとき
\(\small{ \ x^2=4py \ }\)
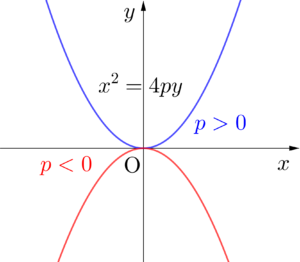
放物線の性質
座標平面上で定点\(\small{ \ \mathrm{F} \ }\)からの距離と、\(\small{ \ \mathrm{F} \ }\)を通らない定直線\(\small{ \ l \ }\)からの距離が等しい点の軌跡が放物線になるんだ。
この定直線のことを準線、定点のことを焦点っていうから覚えておこう。
放物線の方程式
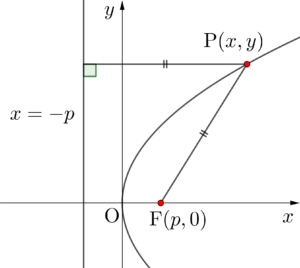
\(\small{ \ \mathrm{F}(p,0) \ }\)を焦点、\(\small{ \ x=-p \ }\)を準線としたとき、放物線の方程式を求めてみよう。
放物線上の点を\(\small{ \ \mathrm{P}(x,y) \ }\)として、準線からの距離と、焦点からの距離が等しいから
\(\small{ \ \left|x-(-p)\right|= \sqrt{(x-p)^2+y^2} \ }\)
両辺を二乗して
\(\small{ \ (x+p)^2=(x-p)^2+y^2 \ }\)
これを整理すると、\(\small{ \ y^2=4px \ }\)になる。
この式を放物線の方程式の標準形っていうんだ。軸については二次関数のときにも習ったけど、焦点と準線を含んで説明すると、焦点を通り、準線に垂直な直線が軸になる。また軸と放物線の交点が頂点になる。
もちろんすでに知ってることだけど、放物線は軸に関して対称だからね。
ちなみに、準線からの距離を\(\small{ \ \left|x-(-p)\right| \ }\)ってしたのは、\(\small{ \ p \ }\)が負の場合は\(\small{ \ x+p \ }\)が負になるから絶対値をとって計算したんだ。
そうすることで、\(\small{ \ p \ }\)が正でも負でもわざわざ場合分けしなくて済むからね。\(\small{ \ p \ }\)の正負によって形が図の様に変わるから覚えておこう。っていっても二次関数のときに上に凸、下に凸で\(\small{ \ x^2 \ }\)の係数の正負が反対になるのは教わっているから理解できるよね。

y軸が軸の放物線
\(\small{ \ y \ }\)軸が軸になる放物線の場合、焦点が\(\small{ \ y \ }\)軸上にあるよね。
焦点を\(\small{ \ (0,p) \ }\)、準線を\(\small{ \ y=-p \ }\)とすると
\(\small{ \ \left|y-(-p)\right|=\sqrt{x^2+(y-p)^2} \ }\)
両辺を二乗して
\(\small{ \ (y+p)^2=x^2+(y-p)^2 \ }\)
これを整理して、\(\small{ \ x^2=4py \ }\)になるよね。

中学生のときに初めて習った二次関数\(\small{ \ y=ax^2 \ }\)は
\(\small{ \ x^2= \displaystyle\frac{y}{a}=4\cdot\displaystyle\frac{1}{4a}y \ }\)になるから、焦点\(\small{ \ \left(0,\displaystyle\frac{1}{4a}\right) \ }\)、準線\(\small{ \ y=-\displaystyle\frac{1}{4a} \ }\)の放物線ってことになるんだ。
平行移動する場合も、準線と焦点も一緒に平行移動してあげればいいよね。そのあたりについては以前学習した二次関数の平行移動で復習しておこう。
-

二次関数のグラフの平行移動
平方形の移動と一般形の移動について詳しく解説しています。
続きを見る
次の条件を満たす点\(\small{ \ \mathrm{P} \ }\)の軌跡を求めよ。
(1) \(\small{ \ (2,4) \ }\)と\(\small{ \ x \ }\)軸から等距離にある点\(\small{ \ \mathrm{P} \ }\)
(2)\(\small{ \ x \ }\)軸に接し、円\(\small{ \ x^2+(y-5)^2=1 \ }\)に外接する円の中心\(\small{ \ \mathrm{P} \ }\)
(1)\(\small{ \ (2,4) \ }\)と\(\small{ \ x \ }\)軸から等距離にあるから
\(\small{ \ \sqrt{(x-2)^2+(y-4)^2}=\left|y \right| \ }\)
両辺二乗して
\(\small{ \ (x-2)^2+(y-4)^2=y^2 \ }\)
\(\small{ \ y=\displaystyle\frac{1}{8}(x-2)^2+2 \ }\)
(2)外接する二つの円の中心の距離は二つの円の半径の和に等しいから
\(\small{ \ \sqrt{x^2+(y-5)^2}=1+y \ }\)
\(\small{ \ x^2+(y-5)^2=(1+y)^2 \ }\)
\(\small{ \ y=\displaystyle\frac{1}{12}x^2+2 \ }\)

この二次曲線の単元は「図形と方程式」の延長上にあると思ってもらうといいかな。
数学Ⅱだと軌跡を求めよって問題の答えは、円か直線、放物線だったけど、二次曲線を含めれば、これに楕円、双曲線、\(\small{ \ x \ }\)軸に平行な軸を持つ放物線が加わるからね。
この単元を学習する前に図形と方程式の軌跡を復習しておこう。
放物線の接線の方程式
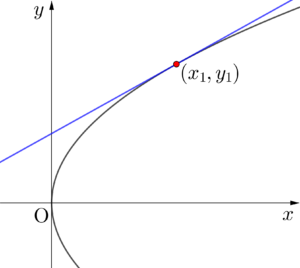
\(\small{ \ y^2=4px \ }\)上の点\(\small{ \ (x_1,y_1) \ }\)の接線の方程式を考えよう。
\(\small{ \ y^2=4px \ }\)の両辺を\(\small{ \ x \ }\)で微分すると\(\small{ \ 2yy'=4p \ }\)になるよね。
これは陰関数の微分だよね。忘れている人は一度復習しておこう。
-

陰関数・陽関数と陰関数の微分
陰関数と陽関数の違いや二次曲線の微分について詳しく解説しています。
続きを見る
\(\small{ \ y'=\displaystyle\frac{2p}{y} \ }\)だから、接線の方程式は\(\small{ \ y=\displaystyle\frac{2p}{y_1}(x-x_1)+y_1 \ }\)
接線の方程式の求め方を忘れている人はこっちも復習しておこう。とても大切な式だからね。
-

接線の方程式
曲線上の点における接線の求め方や曲線上にない点から引いた接線の方程式の求め方について解説しています。
続きを見る
接線の式を覚えていれば、それでいいんだけど、ほとんどの問題集や参考書には次の式まで変形してある。
\(\small{ \ \begin{aligned}
y_1y&=2p(x-x_1)+{y_1}^2\\
&=2p(x-x_1)+4px_1\\
&=2p(x+x_1)\end{aligned} \ }\)
こっちの方が見た目がいいかもしれないけど、陰関数の微分がきちんとできていれば問題ないからこの式はそこまで気にしなくて大丈夫だからね。

-

放物線と直線の共有点の求め方
放物線と直線の共有点の座標の求め方について学習します。判別式を利用した接するときの求め方や、解と係数の関係を利用した共有点の問題について解説します。
続きを見る
Point 放物線
①放物線は準線と焦点からの距離が等しい点の軌跡
②焦点\(\small{ \ (p,0) \ }\)、準線\(\small{ \ x=-p \ }\)のとき\(\small{ \ y^2=4px \ }\)
③焦点\(\small{ \ (0,p) \ }\)、準線\(\small{ \ y=-p \ }\)のとき\(\small{ \ x^2=4py \ }\)
④接線の傾きは陰関数の微分を利用
\(\small{ \ xy \ }\)平面において、点\(\small{ \ \mathrm{F}(p,0) \ }\)と\(\small{ \ y \ }\)軸から等距離にある点の軌跡を\(\small{ \ C \ }\)とする。ただし\(\small{ \ p\gt0 \ }\)とする。
(1)\(\small{ \ C \ }\)を表す方程式を求めよ。
(2)\(\small{ \ C \ }\)上の点\(\small{ \ \mathrm{P}(x_0,y_0) \ }\)における接線\(\small{ \ l \ }\)の方程式を求めよ。ただし\(\small{ \ y_0\neq 0 \ }\)とする。
(3)(2)の\(\small{ \ l \ }\)と\(\small{ \ x \ }\)軸の交点を\(\small{ \ \mathrm{Q} \ }\)とするとき、\(\small{ \ \mathrm{FP=FQ} \ }\)であることを証明せよ。
(1)点\(\small{ \ \mathrm{F}(p,0) \ }\)と\(\small{ \ y \ }\)軸から等距離にある\(\small{ \ C \ }\)上の点を\(\small{ \ (x,y) \ }\)とすると
\(\small{ \ \sqrt{(x-p)^2+y^2}=\left|x\right| \ }\)
両辺二乗して
\(\small{ \ (x-p)^2+y^2=x^2 \ }\)
これを整理して、\(\small{ \ y^2=2px-p^2 \ }\)
(2)\(\small{ \ y^2=2px-p^2 \ }\)の両辺を\(\small{ \ x \ }\)で微分すると
\(\small{ \ 2y\displaystyle\frac{dy}{dx}=2p \ }\)
\(\small{ \ \displaystyle\frac{dy}{dx}=\displaystyle\frac{p}{y} \ }\)
よって、\(\small{ \ \mathrm{P}(x_0,y_0) \ }\)における接線の方程式は
\(\small{ \ y=\displaystyle\frac{p}{y_0}(x-x_0)+y_0 \ }\)
\(\small{ \ y=\displaystyle\frac{p}{y_0}x-\displaystyle\frac{px_0}{y_0}+y_0 \ }\)
(3)\(\small{ \ \displaystyle\frac{p}{y_0}x-\displaystyle\frac{px_0}{y_0}+y_0=0 \ }\)
\(\small{ \ \begin{aligned}
x&=\displaystyle\frac{y_0}{p}\left(\displaystyle\frac{px_0}{y_0}-y_0\right)\\
&=x_0-\displaystyle\frac{{y_0}^2}{p}\\
&=x_0-\displaystyle\frac{2px_0-p^2}{p}\\
&=p-x_0
\end{aligned} \ }\)
\(\small{ \ \mathrm{FQ}=\left|(p-x_0)-p\right|=\left|x\right| \ }\)
\(\small{ \ \begin{aligned}
\mathrm{FP}&=\sqrt{(x_0-p)^2+{y_0}^2}\\
&=\sqrt{{x_0}^2-2px_0+p^2+2px_0-p^2}\\
&=\sqrt{{x_0}^2}=\left|x\right| \end{aligned} }\)
\(\small{ \ \therefore \mathrm{FP=FQ} \ }\)