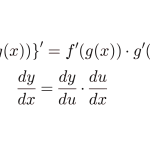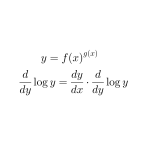こんにちは、リンス(@Lins016)です。
今回は陰関数・陽関数と陰関数の微分について学習していこう。
陰関数と陽関数
陰関数と陽関数って聞いたことあるかな?教科書にはきちんとした語句としては掲載されてないかもしれないけど、一般的にそう呼ばれている関数があるんだ。
実際高校数学では陰関数なのか陽関数なのかってことはそんなに気にしなくてもいいんだけど、「微分したときの形がどんな形になるのか」ってことと「どうしてその形になるのか」を考えてほしい。それじゃ始めていこう。
陰関数表示
\(\small{ \ f(x, \ y)=0 \ }\)
陽関数表示
\(\small{ \ y=f(x) \ }\)
微分
\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で微分\(\small{ \ \displaystyle\frac{dy}{dx}(y') \ }\)
\(\small{ \ y^2 \ }\)を\(\small{ \ x \ }\)で微分\(\small{ \ 2y\cdot\displaystyle\frac{dy}{dx}(2yy') \ }\)
陰関数と陽関数
陰関数と陽関数とは『\(\small{ \ y \ }\)が\(\small{ \ x \ }\)の関数のとき、その関数の関係が\(\small{ \ y=f(x) \ }\)の形であれば陽関数表示、\(\small{ \ f(x, \ y)=0 \ }\)の形であれば陰関数表示』のことなんだ。
つまり陰関数とは『\(\small{ \ f(x, \ y)=0 \ }\)の形になっている関数』のこと。例えば\(\small{ \ x^2+y^2-4=0 \ }\)とかね。
これに対して陽関数とは『\(\small{ \ y=f(x) \ }\)の形になっているの関数』のこと。例えば\(\small{ \ y=x^3-x+1 \ }\)とかね。
正確には陰関数表示、陽関数表示ってことになるんだけど、一般的に陰関数、陽関数って使われているんだ。
でもここで気付くよね。この陽関数を移項すれば\(\small{ \ f(x, \ y)=0 \ }\)の形にできるって。\(\small{ \ y=x^3-x+1 \ }\)なら\(\small{ \ x^3-x-y+1=0 \ }\)ってね。こうなるとこれは陰関数表示ってことになるんだ。
だから表示の仕方ってことになるんだけど、一般的に陰関数表示の\(\small{ \ f(x, \ y)=0 \ }\)は陰関数、陽関数表示の\(\small{ \ y=f(x) \ }\)は陽関数って言われるんだ。
でも陽関数は移項することで陰関数にすることができるけど、陰関数は陽関数に必ずできるとは言えないんだ。
例えば\(\small{ \ x^2+y^2-4=0 \ }\)は\(\small{ \ y=\pm\sqrt{4-x^2} \ }\)って変形できるから陰関数から陽関数に変形できるよね。だけど、\(\small{ \ x^2+xy+y^3+y-3=0 \ }\)のような関数は\(\small{ \ y=f(x) \ }\)の形に変形するのは難しい。
しかも\(\small{ \ x^2+y^2-4=0 \ }\)を\(\small{ \ y=\pm\sqrt{4-x^2} \ }\)に変形したのだって、元の\(\small{ \ x^2+y^2-4=0 \ }\)の方がきれいな形だしね。
それに陰関数って関数とは言えない場合もあるんだ。
\(\small{ \ (x-2)^2+(y-2)^2-4=0 \ }\)なら関数だけど\(\small{ \ (x-2)^2+(y-2)^2=0 \ }\)なら\(\small{ \ (x, \ y)=(2, \ 2) \ }\)になるから点だよね。つまり\(\small{ \ f(x, \ y)=0 \ }\)は必ずしも関数になるとは限らないってことなんだ。
陰関数と陽関数(正確には陰関数表示と陽関数表示)ってなんとなくわかったけど、だから何って言いたくなるよね。
そう別にここまではなんとなく理解してもらえればよくて、重要なのは、このあとこれを微分するところなんだ。
陰関数の微分
陽関数は\(\small{ \ y=f(x) \ }\)の形だったから数学Ⅱの微分や、数学Ⅲで出題される微分のほとんどがこの形だよね。
つまり微分した導関数は\(\small{ \ \displaystyle\frac{dy}{dx}=f'(x) \ }\)になるから、導関数は\(\small{ \ x \ }\)だけで表されるんだ。
これに対して、陰関数の微分について考えてみよう。
このとき陰関数って言っても陽関数を陰関数表示に変形したものじゃなくて、あらかじめ陰関数表示されているようなものね。
しかも高校数学で出題されるようなものに限定して考えてみよう。高校数学で陰関数表示されている関数は
円(例\(\small{ \ x^2+y^2-16=0 \ }\))
楕円(例\(\small{ \ 4x^2+y^2-16=0 \ }\))
双曲線(例\(\small{ \ 4x^2-y^2-16=0 \ }\))
放物線(例\(\small{ \ y^2-4x=0 \ }\))
つまりいわゆる二次曲線が陰関数表示されているのに気付くよね。
そう重要なのはここなんだ。どういうことかって言うと、\(\small{ \ y=f(x) \ }\)を微分して\(\small{ \ \displaystyle\frac{dy}{dx}=f'(x) \ }\)を求めて、その\(\small{ \ x \ }\)に\(\small{ \ 1 \ }\)を代入するとその値は\(\small{ \ y=f(x) \ }\)の\(\small{ \ x=1 \ }\)における接線の傾き(微分係数)になるんだったよね。
それって\(\small{ \ y=f(x) \ }\)のグラフが\(\small{ \ x \ }\)の値\(\small{ \ 1 \ }\)つにつき\(\small{ \ y \ }\)の値が\(\small{ \ 1 \ }\)つ定まるからだよね。
でも二次曲線はそうはいかないよね。だって例えば\(\small{ \ x^2+y^2-16=0 \ }\)の場合、\(\small{ \ x=2 \ }\)のとき\(\small{ \ y=\pm2\sqrt{3} \ }\)になって\(\small{ \ (x, \ y)=(2, \ 2\sqrt{3}) \ }\)と\(\small{ \ (2, \ -2\sqrt{3}) \ }\)で接線の傾きって違うよね。
このことから陰関数表示(特に高校数学における二次曲線)は導関数\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)が\(\small{ \ x \ }\)だけの式じゃなくて、\(\small{ \ x \ }\)も\(\small{ \ y \ }\)も含んだ式になってるって言えそうだよね。
そう、この円の場合導関数\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)は\(\small{ \ x \ }\)と\(\small{ \ y \ }\)を含んだ式になるんだ。
だって\(\small{ \ x \ }\)が決まっても\(\small{ \ y \ }\)が\(\small{ \ 1 \ }\)つに定まらない二次曲線の場合、導関数が\(\small{ \ x \ }\)だけの式になるわけないよね。
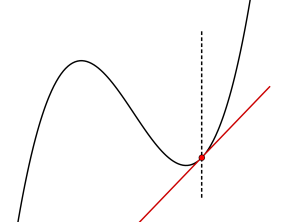
\(\small{ \ y=f(x) \ }\)の場合
\(\small{ \ x \ }\)が定まると接線の傾きが決定する
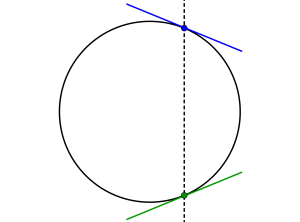
\(\small{ \ f(x, \ y)=0 \ }\)の二次曲線の場合
\(\small{ \ x \ }\)と\(\small{ \ y \ }\)が定まると接線の傾きが決定する
陰関数の微分のやり方
それじゃ陰関数表示(高校数学における二次曲線)の微分のやり方を学習していこう。
\(\small{ \ x^2+y^2-r^2=0 \ }\)を\(\small{ \ x \ }\)で微分してみよう。
\(\small{ \ x^2 \ }\)を\(\small{ \ x \ }\)で微分すると\(\small{ \ 2x \ }\)になるよね。でも\(\small{ \ y^2 \ }\)は単純に\(\small{ \ x \ }\)で微分できないから少し工夫が必要なんだ。
\(\small{ \ \displaystyle\frac{d}{dx}y^2=\displaystyle\frac{dy}{dx}\cdot\displaystyle\frac{d}{dy}y^2=\displaystyle\frac{dy}{dx}\cdot 2y \ }\) になるんだ。つまり\(\small{ \ 2yy' \ }\)ってことね。合成関数の微分や対数微分法で学習したやり方と同じ。
-

合成関数の導関数(微分)の定義
合成関数の微分の式について詳しく解説しています。
続きを見る
-

対数微分法
log yを微分したらy'/yになる理由など詳しく解説しています。
続きを見る
\(\small{ \ r^2 \ }\)は定数だから\(\small{ \ x \ }\)で微分すると\(\small{ \ 0 \ }\)。
だから\(\small{ \ x^2+y^2-r^2=0 \ }\)を\(\small{ \ x \ }\)で微分すると\(\small{ \ 2x+2yy'=0 \ }\)になるから、これを変形して\(\small{ \ y'=-\displaystyle\frac{x}{y} \ }\)になるよね。
確かに導関数に\(\small{ \ x, \ y \ }\)ともに入ってるよね。
つまり\(\small{ \ g(y) \ }\)を\(\small{ \ x \ }\)で微分すると
\(\small{\begin{eqnarray} \ &&\displaystyle\frac{d}{dx}g(y)\\
&=&\displaystyle\frac{dy}{dx}\cdot\displaystyle\frac{d}{dy}g(y)\\
&=&\displaystyle\frac{dy}{dx}g'(y)\\
&=&g'(y)y' \ \end{eqnarray}}\)
ってなるから覚えておこう。
だから陰関数の微分は、\(\small{ \ x \ }\)は普通に微分して\(\small{ \ y \ }\)は\(\small{ \ y \ }\)で微分したものに\(\small{ \ y' \ }\)をかける。それを\(\small{ \ y'= \ }\)の形に整理すれば陰関数の導関数を求めることができるんだ。

-

円の接線の方程式の証明
円の接線の方程式の公式について解説しています。
続きを見る
次の関数について\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)を求めよ。
(1)\(\small{ \ y^2=4x \ }\)
(2)\(\small{ \ x^2-\displaystyle\frac{y^2}{9}=1 \ }\)
(3)\(\small{ \ x^3+xy+y^2=0 \ }\)
(1)\(\small{ \ y^2=4x \ }\)
両辺を\(\small{ \ x \ }\)で微分すると
\(\small{ \ 2yy'=4 \ }\)
\(\small{ \ \therefore y'=\displaystyle\frac{2}{y} \ }\)
(2)\(\small{ \ x^2-\displaystyle\frac{y^2}{9}=1 \ }\)
両辺を\(\small{ \ x \ }\)で微分すると
\(\small{ \ 2x-\displaystyle\frac{2yy'}{9}=0 \ }\)
\(\small{ \ \therefore y'=\displaystyle\frac{9x}{y} \ }\)
(3)\(\small{ \ x^3+xy+y^2=0 \ }\)
両辺を\(\small{ \ x \ }\)で微分すると
\(\small{ \ 3x^2+1\cdot y+x\cdot y'+2yy'=0 \ }\)
\(\small{ \ \therefore y'=-\displaystyle\frac{3x^2+y}{x+2y} \ }\)

Point 陰関数・陽関数と陰関数の微分
①\(\small{ \ f(x, \ y)=0 \ }\)は陰関数、\(\small{ \ y=f(x) \ }\)は陽関数
②陽関数の導関数は\(\small{ \ x \ }\)だけ含まれる
③陰関数の導関数は\(\small{ \ x,y \ }\)が含まれる