微分の計算

こんにちは、リンス(@Lins016)です。
今回は微分の計算について学習していこう。

合成関数を利用した微分の計算

数学Ⅲの入試に出てくる微分の計算ってそんな簡単な微分の計算は出てこない。

今回合成関数を利用した微分の計算を学習するから、この方法を確実に覚えてどんな問題も解けるようにしていこう。

微分の公式を覚える

まずは\(\small{ \ \sin x \ }\)を微分したら\(\small{ \ \cos x \ }\)になるっていうような微分の公式を全部確実に覚えよう。これを覚えてなかったら\(\small{ \ 0 \ }\)点って言ってもいいぐらいだからね。

・整関数
\(\small{ \ \left(x^n\right)'=nx^{n-1} \ }\)
※\(\small{ \ n \ }\)が分数の場合も利用可

・三角関数
\(\small{ \ \left(\sin x\right)'=\cos x \ }\)
\(\small{ \ \left(\cos x\right)'=-\sin x \ }\)
\(\small{ \ \left(\tan x\right)'=\displaystyle\frac{1}{\cos^2 x} \ }\)

・指数関数
\(\small{ \ \left(e^x\right)'=e^x \ }\)
\(\small{ \ \left(a^x\right)=a^x \log a \ }\)

・対数関数
\(\small{ \ \left(\log x\right)'=\displaystyle\frac{1}{x} \ }\)
\(\small{ \ \left(\log_a x\right)'=\displaystyle\frac{1}{x\log a} \ }\)

・積の微分
\(\small{ \ \left(f(x)g(x)\right)'=f'(x)g(x)+f(x)g'(x) \ }\)

・商の微分
\(\small{ \ \left(\displaystyle\frac{f(x)}{g(x)}\right)'=\displaystyle\frac{f'(x)g(x)-f(x)g'(x)}{\left\{g(x)\right\}^2 } \ }\)

この微分法の証明についても確認しておこう。

微分の記号dy/dx

数学IIで微分を教わったときは、\(\small{ \ y \ }\)を微分すると\(\small{ \ y' \ }\)、\(\small{ \ f(x) \ }\)を微分すると\(\small{ \ f'(x) \ }\)って書くことがほとんどだったよね。

でも数学IIIでは「微分する」って言葉の前に「\(\small{ \ x \ }\)で微分する」や「\(\small{ \ t \ }\)で微分する」っていうようにどの文字で微分するかってことが必要になる場合があるんだ。そうなったときに\(\small{ \ y' \ }\)はどの文字で\(\small{ \ y \ }\)を微分したかわからないよね。

だから\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で微分するって記号を\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)って書くことにするんだ。
\(\small{ \ \displaystyle\frac{d}{dx} \ }\)って記号が「\(\small{ \ x \ }\)で微分する」ってことになるから、\(\small{ \ \displaystyle\frac{d}{dx}y \ }\)で「\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で微分する」ってことになって、\(\small{ \ \displaystyle\frac{d}{dx}y \ }\)を\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)って書くんだ。

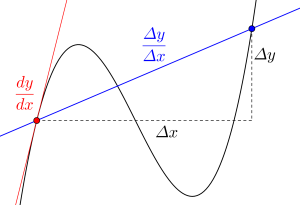
高校の範囲を超えちゃうけど、\(\small{ \ \varDelta \ }\)(大文字のデルタ)は差を表す記号として、\(\small{ \ \delta \ }\)(小文字のデルタ)は無限小の変化を表す記号として、\(\small{ \ d \ }\)は無限小の差(微分)を表す記号として使われるからね。

合成関数の微分の導入dy/dx=dy/du・du/dx

さあ、ここから今回の記事の本題に入っていくよ。

まずは\(\small{ \ y=(3x^2+x+1)^3 \ }\)の微分について考えてみよう。展開して微分すればいいけど、それだとちょっと大変だよね。

だから\(\small{ \ u=3x^2+x+1 \ }\)っておいて微分を考えることにするんだ。\(\small{ \ u=3x^2+x+1 \ }\)だから\(\small{ \ y=u^3 \ }\)になるよね。

でもこれって\(\small{ \ y \ }\)と\(\small{ \ u \ }\)の式だから\(\small{ \ y \ }\)を\(\small{ \ u \ }\)で微分することしかできないよね。
だから\(\small{ \ y=u^3 \ }\)を\(\small{ \ u \ }\)で微分すると\(\small{ \ \displaystyle\frac{dy}{du}=3u^2 \ }\)になる。

でも求めたいのは\(\small{ \ y=(3x^2+x+1)^3 \ }\)を\(\small{ \ x \ }\)で微分した\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)だから\(\small{ \ \displaystyle\frac{dy}{du}=3u^2 \ }\)だと答えになってないよね。ここでこの式を覚えててほしい。

\(\small{ \ \displaystyle\frac{dy}{dx}= \displaystyle\frac{dy}{du}\cdot\displaystyle\frac{du}{dx} \ }\)

これは\(\small{ \ y \ }\)を\(\small{ \ u \ }\)で微分した式と\(\small{ \ u \ }\)を\(\small{ \ x \ }\)で微分した式をかけると\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で微分した式になるってことを表した式なんだ。見た目でいうと右辺の\(\small{ \ \displaystyle\frac{dy}{du} \ }\)の分母の\(\small{ \ du \ }\)と\(\small{ \ \displaystyle\frac{du}{dx} \ }\)の分子の\(\small{ \ du \ }\)が約分できる感じになるよね。

ただ、\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)は\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で微分した記号だから、実際は分数じゃないから約分するってことにはならないんだけど、\(\small{ \ \displaystyle\frac{dy}{dx}= \displaystyle\frac{dy}{du}\cdot\displaystyle\frac{du}{dx} \ }\)って式は成り立つから、見かけ上\(\small{ \ du \ }\)を約分したように考えていいんだ。

詳しくは次の記事を確認しておこう。

だから\(\small{ \ y=(3x^2+x+1)^3 \ }\)を\(\small{ \ u=3x^2+x+1 \ }\)っておいて、
\(\small{ \ y=u^3 \ }\)から\(\small{ \ \displaystyle\frac{dy}{du}=3u^2 \ }\)、
\(\small{ \ u=3x^2+x+1 \ }\)から\(\small{ \ \displaystyle\frac{du}{dx}=6x+1 \ }\)
求める答えは\(\small{ \ \displaystyle\frac{dy}{dx}= \displaystyle\frac{dy}{du}\cdot\displaystyle\frac{du}{dx} \ }\)だから
\(\small{\begin{eqnarray} \ \displaystyle\frac{dy}{dx}&=&\displaystyle\frac{dy}{du}\cdot\displaystyle\frac{du}{dx} \\[5pt] &=&3u^2(6x+1)\\[5pt] &=&3(6x+1)(3x^2+x+1)^2 \ \end{eqnarray}}\)

合成関数の微分の利用と公式の関係

合成関数を利用するっていうことは\(\small{ \ x \ }\)の式を\(\small{ \ u \ }\)の式に変更するってことになるんだけど、どんな\(\small{ \ x \ }\)の式を\(\small{ \ u \ }\)っておけばいいのか、\(\small{ \ y=\sin^2\sqrt{\mathstrut x^2+x+1} \ }\)の微分を考えながら合成関数の利用方法を覚えていこう。

\(\small{ \ u=\sin\sqrt{\mathstrut x^2+x+1} \ }\)っておくと
\(\small{ \ y=u^2\cdots① \ }\)になるよね。
これは\(\small{ \ y \ }\)が整関数の式になったから簡単に微分できるよね。
\(\small{ \ \displaystyle\frac{dy}{du}=2u \ }\)

次に\(\small{ \ u=\sin\sqrt{\mathstrut x^2+x+1} \ }\)を\(\small{ \ x \ }\)で微分するんだけど、このままじゃまだ簡単に微分できないからもう一度文字をおこう。

\(\small{ \ t=\sqrt{\mathstrut x^2+x+1} \ }\)っておくと
\(\small{ \ u=\sin t \cdots ② \ }\)になるよね。
これは\(\small{ \ u \ }\)が三角関数の式になったから簡単に微分できるよね。\(\small{ \ u \ }\)を\(\small{ \ t \ }\)で微分しよう。
\(\small{ \ \displaystyle\frac{du}{dt}=\cos t \ }\)

\(\small{ \ t=\sqrt{\mathstrut x^2+x+1} \ }\)を微分するんだけど、これぐらいだったら簡単にできる人もいると思うけど、今回は丁寧にもう一度別な文字でおいて微分してみよう。

\(\small{ \ r=x^2+x+1 \ }\)っておくと
\(\small{ \ t=\sqrt{r}=r^{\frac{1}{2}}\cdots ③ \ }\)になるよね。
これは\(\small{ \ r \ }\)が整関数\(\small{ \ (x^n)'=nx^{n-1} \ }\)の式になったから簡単に微分できるよね。
\(\small{ \ \displaystyle\frac{dt}{dr}=\displaystyle\frac{1}{2}r^{-\frac{1}{2}}=\displaystyle\frac{1}{2\sqrt{r}} \ }\)

最後に\(\small{ \ r=x^2+x+1\cdots ④ \ }\)を微分すればいいから
\(\small{ \ \displaystyle\frac{dr}{dx}=2x+1 \ }\)

求める答えは\(\small{ \ \displaystyle\frac{dy}{dx}=\displaystyle\frac{dy}{du}\cdot\displaystyle\frac{du}{dt}\cdot\displaystyle\frac{dt}{dr}\cdot\displaystyle\frac{dr}{dx} \ }\)になるから

この問題ってたくさん文字をおかないといけなくて大変だよね。しかも、どの文字をどうやっておけばいいかわかりにくいもんね。だから文字をおく上で\(\small{ \ 1 \ }\)つのルールを作っておこう。

そのルールっていうのは
「文字を置き換えたとき、元の式が公式の形と同じになる」
ってことなんだ。

今回文字は始めに\(\small{ \ y \ }\)を\(\small{ \ u \ }\)で表して、次に\(\small{ \ u \ }\)を\(\small{ \ t \ }\)で表して、次に\(\small{ \ t \ }\)を\(\small{ \ r \ }\)で表したけど、この文字を置き換えたときの式を確認すると、
\(\small{ \ y=u^2\cdots① \ }\)
\(\small{ \ u=\sin t \cdots ② \ }\)
\(\small{ \ t=\sqrt{r}=r^{\frac{1}{2}}\cdots ③ \ }\)
\(\small{ \ r=x^2+x+1\cdots ④ \ }\)

この\(\small{ \ 4 \ }\)つの式を見てわかるけど、この\(\small{ \ 4 \ }\)つの式って微分の公式がそのまま利用できる形になってるよね。

そう、わざわざ別な文字で置き換えるっていうのは公式の形にするために置き換えるんだ。だから公式は\(\small{ \ x \ }\)で表してあるけど、置き換えた文字で公式の形になるようにしよう。

微分の公式の利用

実はどんな関数でもこの合成関数の微分の考え方を使えば微分出来る。

例えば\(\small{ \ y=\sin 3x \ }\)の微分も
\(\small{ \ y=\sin u, \ u=3x \ }\)
\(\small{ \ \displaystyle\frac{dy}{du}=\cos u, \ \displaystyle\frac{du}{dx}=3 \ }\)
\(\small{\begin{eqnarray} \ \displaystyle\frac{dy}{dx}&=&\displaystyle\frac{dy}{du}\cdot\displaystyle\frac{du}{dx}\\[5pt] &=&3\cos u\\[5pt] &=&3\cos 3x \ \end{eqnarray}}\)
って計算できるよね。

ただ、実際これぐらいの式だったら合成関数の計算式\(\small{ \ \displaystyle\frac{dy}{du}\cdot\displaystyle\frac{du}{dx} \ }\)をわざわざ書かなくても頭の中で計算できるようになって欲しいってことなんだ。

\(\small{ \ y=\sin^2\sqrt{x^2+x+1} \ }\)のような複雑な式なら\(\small{ \ 1 \ }\)つずつおいて計算していくのがいいけど、\(\small{ \ 1 \ }\)度おけば微分出来る式は頭の中でできるように練習しよう。

\(\small{ \ y=e^{x^2} \ }\)だったら\(\small{ \ x^2=u \ }\)っておいて\(\small{ \ y=e^u \ }\)と\(\small{ \ u=x^2 \ }\)を微分すればいいから
\(\small{ \ \displaystyle\frac{dy}{dx}=2xe^{x^2} \ }\)

たくさん練習してスムーズに微分できるようにしておこう。

とにかく公式の形に変形するしよう。積の微分や商の微分を利用する場合も同じだから、丁寧に計算していこう。

Point 微分の計算

①公式を確実に覚える
②複雑な形は文字を置いて公式の形にする

数学Ⅲで対数を微分するときは底をあらかじめ\(\small{ \ e \ }\)にしておく方が計算しやすいと思うから、微分する前に底の変換をしておこう。