こんにちは、リンス(@Lins016)です。
今回は媒介変数表示の微分について学習していこう。
媒介変数とは
媒介変数って教科書では数学Ⅲのいろいろな曲線できちんと教わるんだけど、実際は数学Ⅱの図形と方程式で学習してるんだ。\(\small{ \ x, \ y \ }\)の方程式で表される曲線以外にも\(\small{ \ (x, \ y)=\left(f(t), \ g(t)\right) \ }\)の形で表される曲線があったよね。
これを曲線の媒介変数表示っていって、変数\(\small{ \ t \ }\)を媒介変数とかパラメータっていうから覚えておこう。
\(\small{ \ (x, \ y)=\left(f(t), \ g(t)\right) \ }\)のとき
\(\small{ \ \displaystyle\frac{dy}{dx}=\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}}=\displaystyle\frac{g'(t)}{f'(t)} \ }\)
\(\small{\begin{eqnarray} \ \displaystyle\frac{d^2y}{dx^2}&=&\displaystyle\frac{d}{dx}\cdot\displaystyle\frac{dy}{dx}\\
&=&\displaystyle\frac{dt}{dx}\cdot\displaystyle\frac{d}{dt}\left(\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}}\right)\\
&=&\displaystyle\frac{1}{\displaystyle\frac{dx}{dt}}\cdot\displaystyle\frac{d}{dt}\left(\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}}\right) \ \end{eqnarray}}\)
媒介変数表示の軌跡
数学Ⅱの図形と方程式の単元で媒介変数表示された曲線の軌跡を求める方法を学習したんだけど、忘れている人は一度確認しておこう。
要するに「媒介変数を消去して、\(\small{ \ x, \ y \ }\)の式に変形しよう」って言うのが数学Ⅱの媒介変数表示の曲線だったけど、媒介変数を消去できないものだってあるんだ。
例えば\(\small{ \ x=\theta-\sin \theta, \ y=1-\cos\theta }\)とかだと、\(\small{ \ x, \ y \ }\)だけの式にしようとしてもできないよね。
でも曲線だから当然その曲線の接線の傾きを表す関数\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)は存在するはず。
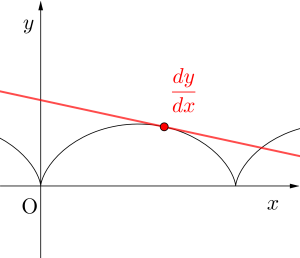
そんな時は\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)も媒介変数を利用して表すんだ。媒介変数表示の微分って言ってもそんなに難しくないから、どうやって微分するのか覚えていこう。
媒介変数表示の微分
\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で微分する記号って\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)だったけど、媒介変数表示の曲線は\(\small{ \ (x, \ y)=\left(f(t), \ g(t)\right) \ }\)の形になっているから、\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で直接微分できないよね。
だから\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)を変形して値を求めるんだ。
\(\small{ \ \displaystyle\frac{dy}{dx}=\displaystyle\frac{dt}{dx}\cdot\displaystyle\frac{dy}{dt}=\displaystyle\frac{1}{\displaystyle\frac{dx}{dt}}\cdot\displaystyle\frac{dy}{dt}=\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}} \ }\)
\(\small{ \ x \ }\)も\(\small{ \ y \ }\)も\(\small{ \ t \ }\)の式だから\(\small{ \ t \ }\)で微分しないといけないよね。だから\(\small{ \ x \ }\)を\(\small{ \ t \ }\)で微分した値\(\small{ \ \displaystyle\frac{dx}{dt} \ }\)と\(\small{ \ y \ }\)を\(\small{ \ t \ }\)で微分した値\(\small{ \ \displaystyle\frac{dy}{dt} \ }\)を利用して\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)を求めよう。
関数\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=a\log t\\
y=\displaystyle\frac{a}{2}\left(t+\displaystyle\frac{1}{t}\right)
\end{array}
\right.
\end{eqnarray} \ }\)について\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)を\(\small{ \ t \ }\)の関数として表したものと、\(\small{ \ x \ }\)の関数として表したものをそれぞれ求めよ。
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=a\log t\\
y=\displaystyle\frac{a}{2}\left(t+\displaystyle\frac{1}{t}\right)
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ \displaystyle\frac{dy}{dt}=\displaystyle\frac{a}{2}\left(1-\displaystyle\frac{1}{t^2}\right) \ }\)
\(\small{ \ \displaystyle\frac{dx}{dt}=\displaystyle\frac{a}{t} \ }\)
\(\small{\begin{eqnarray} \ \displaystyle\frac{dy}{dx}&=&\displaystyle\frac{ \displaystyle\frac{dy}{dt}}{ \displaystyle\frac{dx}{dt}}\\
&=&\displaystyle\frac{\displaystyle\frac{a}{2}\left(1-\displaystyle\frac{1}{t^2}\right)}{\displaystyle\frac{a}{t}}\\
&=&\displaystyle\frac{1}{2}\left(t-\displaystyle\frac{1}{t}\right) \ \end{eqnarray}}\)
\(\small{ \ x=a\log t \ }\)より\(\small{ \ t=e^{\frac{x}{a}} \ }\)
\(\small{\begin{eqnarray} \ \displaystyle\frac{dy}{dx}&=&\displaystyle\frac{1}{2}\left(t-\displaystyle\frac{1}{t}\right)\\
&=&\displaystyle\frac{1}{2}\left(e^{\frac{x}{a}}-e^{-\frac{x}{a}}\right) \ \end{eqnarray}}\)

媒介変数表示の2階微分
次に\(\small{ \ \displaystyle\frac{d^2y}{dx^2} \ }\)の記号について考えてみよう。
この記号って\(\small{ \ \displaystyle\frac{d}{dx}\left(\displaystyle\frac{dy}{dx}\right) \ }\)ってことだから\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で微分したものをもう一度\(\small{ \ x \ }\)で微分するって記号なんだ。つまり\(\small{ \ y \ }\)を\(\small{ \ x \ }\)で\(\small{ \ 2 \ }\)階微分するってことなんだ。

\(\small{ \ y=x^3 \ }\)なら\(\small{ \ \displaystyle\frac{dy}{dx}=3x^2 \ }\)、\(\small{ \ \displaystyle\frac{d^2y}{dx^2}=6x \ }\)って単純に\(\small{ \ 2 \ }\)度微分すればいいんだけど、媒介変数表示の関数だとそうはいかないんだ。
\(\small{ \ \displaystyle\frac{d^2y}{dx^2}=\displaystyle\frac{d}{dx}\left(\displaystyle\frac{dy}{dx}\right) \ }\)だから\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)を\(\small{ \ x \ }\)で微分するんだけど、\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)は媒介変数表示を使った式になるよね。
\(\small{ \ (x, \ y)=\left(f(t), \ g(t)\right) \ }\)なら\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)は媒介変数表示 \(\small{ \ t \ }\)を使った式になる。
だからこの\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)を\(\small{ \ x \ }\)でもう\(\small{ \ 1 \ }\)回微分するって言っても\(\small{ \ t \ }\)の式だから、単純に微分することはできないんだ。
だから、また式を変形して計算していこう。
\(\small{\begin{eqnarray} \ \displaystyle\frac{d^2y}{dx^2}&=&\displaystyle\frac{d}{dx}\left(\displaystyle\frac{dy}{dx}\right)\\
&=&\displaystyle\frac{dt}{dx}\cdot\displaystyle\frac{d}{dt}\left(\displaystyle\frac{dy}{dx}\right)\\
&=&\displaystyle\frac{1}{\displaystyle\frac{dx}{dt}}\cdot\displaystyle\frac{d}{dt}\left(\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}}\right) \ \end{eqnarray}}\)
つまり\(\small{ \ x, \ y \ }\)をそれぞれ\(\small{ \ t \ }\)で微分した式から\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)を求めて、さらにその式をもう一度\(\small{ \ t \ }\)で微分する。そして、その式を\(\small{ \ x \ }\)を\(\small{ \ t \ }\)で微分した式で割ると\(\small{ \ \displaystyle\frac{d^2y}{dx^2} \ }\)が求まるんだ。
媒介変数表示の関数の\(\small{ \ \displaystyle\frac{d^2y}{dx^2} \ }\)を求めるのは計算が大変だから丁寧に計算して答えを求めよう。
\(\small{ \ x=t-\sin t, \ y=1-\cos t \ }\)について\(\small{ \ \displaystyle\frac{d^2y}{dx^2} \ }\)を求めよ。
\(\small{\begin{eqnarray} \ \displaystyle\frac{dy}{dx}&=&\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}}\\
&=&\displaystyle\frac{\sin t}{1-\cos t} \ \end{eqnarray}}\)
\(\small{ \ \displaystyle\frac{d^2y}{dx^2}
=\displaystyle\frac{1}{\displaystyle\frac{dx}{dt}}\cdot\displaystyle\frac{d}{dt}\left(\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}}\right) \ }\)より
\(\small{\begin{eqnarray} \ \displaystyle\frac{d^2y}{dx^2}&=&\displaystyle\frac{1}{1-\cos t}\cdot\left(\displaystyle\frac{\sin t}{1-\cos t}\right)'\\
&=&-\displaystyle\frac{1}{(1-\cos t)^2} \ \end{eqnarray}}\)
Point 媒介変数表示の微分
①\(\small{ \ \displaystyle\frac{dy}{dx} \ }\)は\(\small{ \ x, \ y \ }\)を媒介変数で微分して求める
②\(\small{ \ \displaystyle\frac{d^2y}{dx^2}=\displaystyle\frac{1}{\displaystyle\frac{dx}{dt}}\cdot\displaystyle\frac{d}{dt}\left(\displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}}\right) \ }\)に変形して求める

