こんにちは、リンス(@Lins016)です。
今回は3次関数が極値を持つ条件について学習していこう。
極値は導関数の符号が変化する点
極値は\(\small{ \ f'(x)=0 \ }\)を満たす\(\small{ \ x \ }\)の前後で\(\small{ \ f'(x) \ }\)の符号が変化する点だから、極値を持つ持たないっていうのは\(\small{ \ f'(x)=0 \ }\)が解を持つか持たないかってことを考えることで求めることができる。特によく問われる3次関数\(\small{ \ f(x) \ }\)のグラフとその導関数の関係について考えてみよう。
①\(\small{ \ f'(x)=0 \ }\)が異なる2つの解を持つとき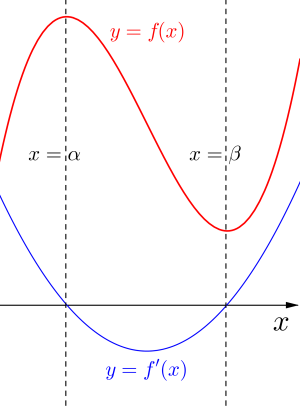
②\(\small{ \ f'(x)=0 \ }\)が重解を持つとき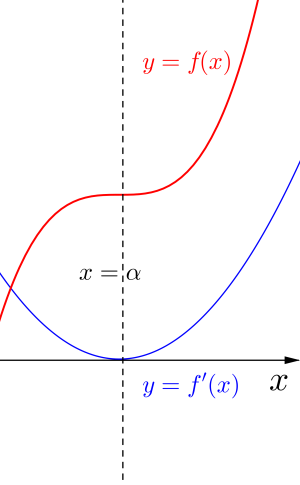
③\(\small{ \ f'(x)=0 \ }\)が解を持たないとき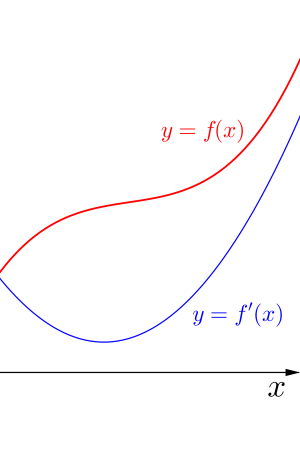
上の図から導関数\(\small{ \ f'(x)=0 \ }\)が異なる2つの解をもてば\(\small{ \ f(x) \ }\)は極値を持つし、解が重解やない場合は単調に増加したり、減少したりして極値を持たないことがわかるよね。この関係を常に頭に入れておこう。
判別式を利用して極値の有無を求める
極値を持つ・持たないっていうのは、微分した\(\small{ \ f'(x)=0 \ }\)が異なる二つの解を持つのか、持たないのかに分かれるから、結局2次関数、特に2次方程式の問題って言えるよね。2次方程式が解を持つ持たないを考えるときは当然、判別式を利用するよね。ただし、2次方程式の場合、解を持つとき判別式\(\small{ \ D \geqq 0 \ }\)、解を持たないとき\(\small{ \ D \lt 0 \ }\)になるけど、極値を考える場合、極値を持つとき判別式\(\small{ \ D \gt 0 \ }\)で極値を持たないとき\(\small{ \ D \leqq 0 \ }\)になるから注意しよう。
\(\small{ \ f(x)=x^3+ax^2-3ax+4 \ }\)について次の条件を満たすような定数\(\small{ \ a \ }\)の値の範囲を求めよ。
(1)\(\small{ \ f(x) \ }\)が単調に増加する
(2)\(\small{ \ f(x) \ }\)が極値をもつ
\(\small{ \ f(x) \ }\)を微分すると
\(\small{ \ f'(x)=3x^2+2ax-3a \ }\)
(1)\(\small{ \ f(x) \ }\)が単調に増加するのは\(\small{ \ f'(x) \ }\)が常に正であればよいので
\(\small{ \ 3x^2+2ax-3a=0 \ }\)の判別式を\(\small{ \ D \ }\)とすると
\(\small{ \ D=(2a)^2-4\cdot 3 \cdot(-3a) \leqq0 \ }\)
\(\small{ \ 4a(a+9) \leqq 0 \ }\)
\(\small{ \ \therefore -9 \leqq a \leqq 0 \ }\)
(2)\(\small{ \ f(x) \ }\)が極値を持つのは\(\small{ \ f'(x)=0 \ }\)が異なる\(\small{ \ 2 \ }\)つの解を持てばよいので
\(\small{ \ 3x^2+2ax-3a=0 \ }\)の判別式を\(\small{ \ D \ }\)とすると
\(\small{ \ D=(2a)^2-4\cdot 3 \cdot(-3a) \gt0 \ }\)
\(\small{ \ 4a(a+9) \gt 0 \ }\)
\(\small{ \ \therefore a \lt-9, \ a \gt 0 \ }\)

Point
①極値を持つ持たないは\(\small{ \ f'(x)=0 \ }\)が異なる2つの解を持つか持たないかを考えよう
②2次方程式が解を持つ持たないは判別式を利用する
\(\small{ \ 3 \ }\)次関数\(\small{ \ f(x)=x^3+ax^2+bx \ }\)は極大値と極小値をもち、それらを区間\(\small{ \ -1 \leqq x \leqq 1 \ }\)でとるものとする。
この条件を満たす実数の組\(\small{ \ (a, \ b) \ }\)の範囲を\(\small{ \ ab \ }\)平面上に図示せよ。
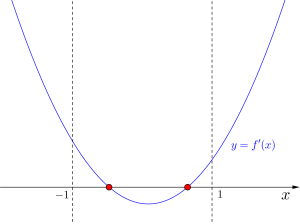
\(\small{ \ f(x)=x^3+ax^2+bx \ }\)が\(\small{ \ -1 \leqq x \leqq 1 \ }\)に極大値と極小値をもつのは、\(\small{ \ -1 \leqq x \leqq 1 \ }\)内に\(\small{ \ f'(x)=0 \ }\)を満たす異なる\(\small{ \ 2 \ }\)つの解が存在すればよいので
\(\small{ \ f'(x)=3x^2+2ax+b=0 \ }\)の判別式を\(\small{ \ D \ }\)とすると
\(\small{ \ D=(2a)^2-4\cdot 3\cdot b \gt 0 \ }\)
\(\small{ \ b \gt \displaystyle \frac{a^2}{3}\cdots① \ }\)
\(\small{ \ \begin{eqnarray}f'(x)&=&3x^2+2ax+b\\
&=&3\left(x+\displaystyle \frac{a}{3}\right)^2-\displaystyle \frac{a^2}{3}+b\end{eqnarray} \ }\)
軸の方程式は\(\small{ \ x=-\displaystyle \frac{a}{3} \ }\)より
\(\small{ \ -1 \leqq -\displaystyle \frac{a}{3} \leqq 1 \ }\)
\(\small{ \ \therefore -3 \leqq a \leqq 3\cdots② \ }\)
\(\small{ \ f'(-1)=3-2a+b \geqq 0 \ }\)
\(\small{ \ \therefore b \geqq 2a-3\cdots③ \ }\)
\(\small{ \ f'(1)=3+2a+b \geqq 0 \ }\)
\(\small{ \ \therefore b \geqq -2a-3\cdots④ \ }\)
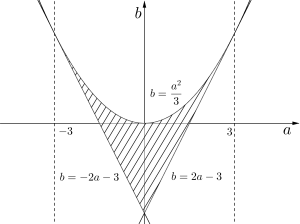
\(\small{ \ ①, \ ②, \ ③, \ ④ \ }\)より
求める範囲は図の斜線部分
ただし、境界線のうち放物線上の点を含まず、他は含む