こんにちは、リンス(@Lins016)です。
今回は二次関数のグラフの対称移動について学習していこう。
二次関数のグラフの対称移動
二次関数に限らず関数の対称移動ってよく利用するから、どう変形すればどのような対称移動になるかきちんと覚えておこう。また、今回は二次関数について学習するけど、この方法は二次関数以外の関数にも利用できるから、他の単元でも使えるように常に頭に入れておこう。
\(\small{ \ y=f(x) \ }\)を対称移動
・\(\small{ \ x \ }\)軸に関して対称移動 \(\small{ \ y=-f(x) \ }\)
・\(\small{ \ y \ }\)軸に関して対称移動 \(\small{ \ y=f(-x) \ }\)
・原点に関して対称移動 \(\small{ \ y=-f(-x) \ }\)
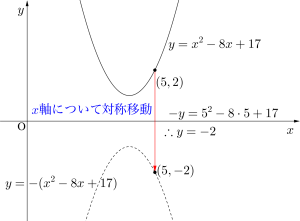
\(\small{ \ x \ }\)軸に関して対称移動
\(\small{ \ y=f(x) \ }\)を\(\small{ \ -y=f(x) \ }\)に変えよう。
点\(\small{ \ (x, \ y) \ }\)を\(\small{ \ x \ }\)軸に関して対称に移動すると、\(\small{ \ x \ }\)座標は同じで、\(\small{ \ y \ }\)座標の符号が入れ替わり、点\(\small{ \ (x, \ -y) \ }\)になるよね。
つまり\(\small{ \ y \ }\)を\(\small{ \ -y \ }\)に書き換えることで、座標が\(\small{ \ x \ }\)軸に関して対称に移動するんだ。
これを\(\small{ \ y=f(x) \ }\)に適用してみると\(\small{ \ -y=f(x) \ }\)になって、\(\small{ \ x \ }\)軸に関して対称移動した関数は、\(\small{ \ y=-f(x) \ }\)になるからね。
\(\small{ \ y \ }\)軸に関して対称移動
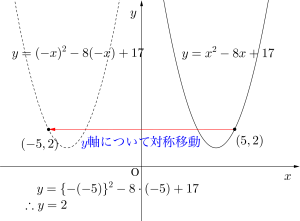
\(\small{ \ y=f(x) \ }\)を\(\small{ \ y=f(-x) \ }\)に変えよう。
点\(\small{ \ (x,y) \ }\)を\(\small{ \ y \ }\)軸に関して対称に移動すると、\(\small{ \ y \ }\)座標は変わらず、\(\small{ \ x \ }\)座標の正負が入れ替わり、点\(\small{ \ (-x, \ y) \ }\)になるよね。
つまり\(\small{ \ x \ }\)を\(\small{-x \ }\)に書き換えることで、座標が\(\small{ \ y \ }\)軸に関して対称に移動するんだ。
これを\(\small{ \ y=f(x) \ }\)に適用してみると\(\small{ \ y=f(-x) \ }\)になって、\(\small{ \ y \ }\)軸に関して対称に移動した関数は、\(\small{ \ y=f(-x) \ }\)になるからね。
特に\(\small{ \ f(x)=f(-x) \ }\)のとき、\(\small{ \ y=f(x) \ }\)は\(\small{ \ y \ }\)軸対称のグラフとなる。\(\small{ \ y \ }\)軸対称の関数を偶関数と言うから覚えておこう。\(\small{ \ y=x^2 \ }\)は偶関数のグラフになるからね。
原点に関して対称移動
\(\small{ \ y=f(x) \ }\)を\(\small{ \ y=-f(-x) \ }\)に変えよう.
点\(\small{ \ (x,y) \ }\)を原点に関して対称に移動すると、\(\small{ \ x,y \ }\)座標ともに正負が入れ替わり、点\(\small{ \ (-x, \ -y) \ }\)になる。
つまり\(\small{ \ x,y \ }\)をそれぞれ\(\small{-x,-y\ }\)に書き換えることで、座標が原点に関して対称に移動するんだ。
これを\(\small{ \ y=f(x) \ }\)に適用してみると\(\small{ \ -y=f(-x) \ }\)となり、原点対称に移動した関数は、\(\small{ \ y=-f(-x) \ }\)になる。これは\(\small{ \ y=f(x) \ }\)を\(\small{ \ x \ }\)軸に関して対称移動した関数を、さらに\(\small{ \ y \ }\)軸に関して対称移動した関数ってことになるからね。

特に\(\small{ \ f(x)=-f(-x) \ }\)のとき、\(\small{ \ y=f(x) \ }\)は原点対称のグラフとなる。原点対称の関数を奇関数と言うから覚えておこう。二次関数のグラフは奇関数になるものはないけど、\(\small{ \ y=x \ }\)や\(\small{ \ y=x^3-x \ }\)とかは奇関数になるからね。
ある放物線を\(\small{ \ y \ }\)軸に関して対称移動し、更に\(\small{ \ x \ }\)軸方向に\(\small{ \ -1 \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ 2 \ }\)移動したら\(\small{ \ y=x^2-4x+6 \ }\)に移った。元の放物線の方程式を求めよ。
\(\small{ \ y=x^2-4x+6 \ }\)のグラフを\(\small{ \ x \ }\)軸方向に\(\small{ \ 1 \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{-2 \ }\)平行移動して、\(\small{ \ y \ }\)軸に関して対称移動したら元の放物線になるから、
まずは\(\small{ \ x \ }\)軸方向に\(\small{ \ 1 \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{-2 \ }\)平行移動して、
\(\small{\begin{eqnarray} y&+&2=(x-1)^2-4(x-1)+6\\
y&=&x^2-6x+9\end{eqnarray}}\)
次に\(\small{ \ y \ }\)軸に関して対称移動すると
\(\small{\begin{eqnarray} y&=&(-x)^2-6(-x)+9\\
&=&x^2+6x+9\end{eqnarray}}\)

Point 二次関数の対称移動
①\(\small{ \ x \ }\)軸に関して対称移動なら\(\small{ \ y \ }\)を\(\small{-y \ }\)に変える
②\(\small{ \ y \ }\)軸に関して対称移動なら\(\small{ \ x \ }\)を\(\small{-x \ }\)に変える
③原点に関して対称移動なら\(\small{ \ x \ }\)を\(\small{-x \ }\)に\(\small{ \ y \ }\)を\(\small{-y \ }\)に変える

