こんにちは、リンス(@Lins016)です。
今回は不等式と領域の図示について学習していこう。
不等式と領域
\(\small{ \ x \ }\)、\(\small{y \ }\)を含む不等式は、その不等式を満たす点\(\small{ \ (x, \ y) \ }\)を領域として図示することができる。
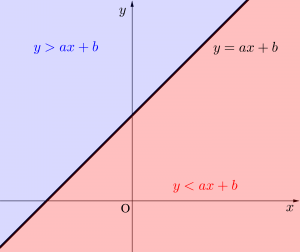
\(\small{ \ y=ax+b \ }\)
\(\small{ \ y \gt ax+b \ }\)
\(\small{ \ y\lt ax+b \ }\)
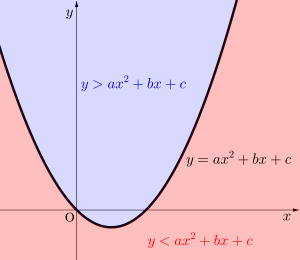
\(\small{ \ y=ax^2+bx+c \ }\)
\(\small{ \ y\gt ax^2+bx+c \ }\)
\(\small{ \ y\lt ax^2+bx+c \ }\)
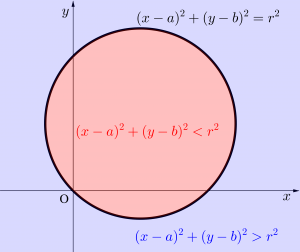
\(\small{ \ (x-a)^2+(y-b)^2=r^2 \ }\)
\(\small{ \ (x-a)^2+(y-b)^2 \gt r^2 \ }\)
\(\small{ \ (x-a)^2+(y-b)^2 \lt r^2 \ }\)
不等式の領域と境界線
まずは不等式とその領域の場所について覚えよう。
直線や放物線の場合、傾きがマイナスでも線より上側が\(\small{ \ y\gt f(x) \ }\)、線より下側が\(\small{ \ y \lt f(x) \ }\)になる。
また、「図示せよ」って問題の場合は図を書いて、その境界線が「含まれる」か「含まれない」か書く必要があるから忘れないようにしよう。
複数の不等式の領域
複数の不等式からなる領域は同時に満たす領域を書こう。
ただし\(\small{ \ \mathrm{AB}\gt 0 \ }\)のような積の形になっている不等式は\(\small{ \ \mathrm{A}\gt 0 \ }\)かつ\(\small{ \ \mathrm{B}\gt 0 \ }\)または\(\small{ \ \mathrm{A}\lt 0 \ }\)かつ\(\small{ \ \mathrm{B}\lt 0 \ }\)の2つのパターンがあるから気をつけよう。
次の不等式の表す領域を図示せよ。
(1)\(\small{ \ (2x-y+1)(x+y-2)\lt 0 \ }\)
(2)\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
x-2y \geqq 1\\
(x-1)^2+(y+1)^2\leqq 4 \
\end{array}
\right.
\end{eqnarray} \ }\)
(3)\(\small{ \ |x|+|y|\leqq 1 \ }\)
(1)(i)\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
2x-y+1\lt 0\\
x+y-2 \gt 0
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{\begin{eqnarray}
\Leftrightarrow\left\{
\begin{array}{l}
y\gt 2x+1\\
y\gt -x+2
\end{array}
\right.
\end{eqnarray} \ }\)
(ii)\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
2x-y+1\gt 0\\
x+y-2 \lt 0
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{\begin{eqnarray}
\Leftrightarrow\left\{
\begin{array}{l}
y\lt 2x+1\\
y\lt -x+2
\end{array}
\right.
\end{eqnarray} \ }\)

(2)\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
x-2y \geqq 1\\
(x-1)^2+(y+1)^2\leqq 4
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{\begin{eqnarray}
\Leftrightarrow\left\{
\begin{array}{l}
y\leqq \displaystyle \frac{1}{2}x-\displaystyle \frac{1}{2}\\
(x-1)^2+(y+1)^2\leqq 4
\end{array}
\right.
\end{eqnarray} \ }\)

(3)(i)\(\small{ \ x\geqq 0 \ }\)、\(\small{ \ y\geqq 0 \ }\)のとき
\(\small{ \ x+y \leqq 1 \ }\)
\(\small{ \ \therefore y \leqq -x+1 \ }\)
(ii)\(\small{ \ x\geqq 0 \ }\)、\(\small{ \ y\lt 0 \ }\)のとき
\(\small{ \ x-y \leqq 1 \ }\)
\(\small{ \ \therefore y \geqq x-1 \ }\)
(iii)\(\small{ \ x \lt 0 \ }\)、\(\small{ \ y\geqq 0 \ }\)のとき
\(\small{ \ -x+y \leqq 1 \ }\)
\(\small{ \ \therefore y \leqq x+1 \ }\)
(iv)\(\small{ \ x \lt 0 \ }\)、\(\small{ \ y\lt 0 \ }\)のとき
\(\small{ \ -x-y \leqq 1 \ }\)
\(\small{ \ \therefore y \geqq -x-1 \ }\)
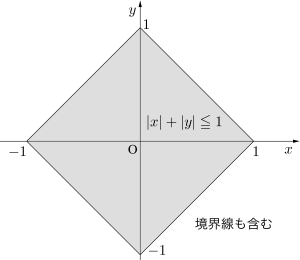

また、絶対値を含む問題は場合分けをして絶対値を外して領域を求めよう。
Point 不等式と領域の図示
①不等式とその領域の場所について覚える
②境界線が「含まれる」「含まれない」も言及しよう。

