こんにちは、リンス(@Lins016)です。
今回は不等式と領域を利用する一次式の最大最小について学習していこう。
制約条件の不等式と領域
領域を用いた最大最小問題は、定期試験なら範囲が決まっているからすぐに判断できるけど、入試で出題されたらいつ使っていいのかわからなくなるよね。
その場合は制約条件から判断しよう。
「(不等式)の条件を満たすとき、次の値の最大値と最小値を求めよ。」のような制約条件が不等式になっていて、かつ不等式が領域として図示できる場合は領域を用いた最大最小を利用しよう。
・解法の手順
①制約条件の不等式の領域を図示する。
まず制約条件の不等式の領域を図示しよう。まずはこれが最初の一歩。図示がうまく出来ないって人はもう一>不等式と領域の図示を確認しておこう。
②与えられた式が最大最小になる点とその点を通る与えられた式と同じ傾きの直線を図に記入する。
傾きに注意して領域を通る\(\small{ \ y \ }\)切片が最大になる直線と\(\small{ \ y \ }\)切片が最小になる直線とその領域と直線が交わる点を図に記入する。
③記入した点の座標を調べる。
②で図に記入した点の座標を調べよう。
-

不等式と領域の図示
こんにちは、リンス(@Lins016)です。 今回は不等式と領域の図示について学習していこう。 不等式と領域 \(\small{ \ x \ }\)、\(\small{y \ }\)を含む不等式は、そ ...
続きを見る
不等式と領域の最大最小の解法の手順を確認
解法の手順を確認しながら\(\small{ \ x\geqq 0\ }\)、\(\small{ \ y \geqq0 \ }\)、\(\small{ \ x+2y\leqq 4 \ }\)、\(\small{ \ x+y\leqq3 \ }\)を満たす\(\small{ \ (x, \ y) \ }\)に対し、\(\small{ \ 2x+3y \ }\)の最大値と最小値を考えてみよう。
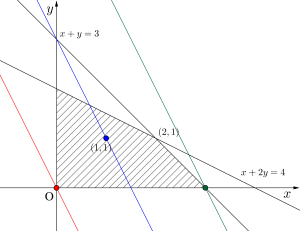
まずは制約条件の\(\small{ \ x\geqq 0\ }\)、\(\small{ \ y \geqq0 \ }\)、\(\small{ \ x+2y\leqq 4 \ }\)、\(\small{ \ x+y\leqq3 \ }\)を図示してみよう。すると図の斜線部分が制約条件を満たす\(\small{ \ (x, \ y) \ }\)になる。
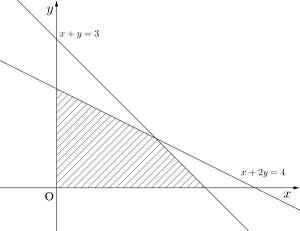
次に\(\small{ \ 2x+3y=k \ }\)とおき、\(\small{ \ y=-\displaystyle \frac{2}{3}x+\displaystyle \frac{1}{3}k \ }\)に変形すると、これは傾き\(\small{ \ -\displaystyle \frac{2}{3} \ }\)、\(\small{ \ y \ }\)切片\(\small{ \ \displaystyle \frac{1}{3}k \ }\)の直線ってことになる。
この直線が領域内を通れば良いから傾き\(\small{ \ -\displaystyle \frac{2}{3} \ }\)の直線を下から上へずらしていくと領域内を直線が通過し始めるのは原点を通るときで、通過し終わるのは\(\small{ \ x+2y=4 \ }\)と\(\small{ \ x+y=3 \ }\)の交点を通るときってことがわかる。
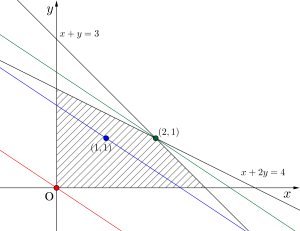
よって\(\small{ \ x+2y=4 \ }\)と\(\small{ \ x+y=3 \ }\)を連立して交点を求めると\(\small{ \ (x, \ y)=(2, \ 1) \ }\)になるから
最大値は\(\small{ \ 2\cdot2+3\cdot1=7 \ }\)\(\small{ \ (x, \ y)=(2, \ 1) \ }\)のとき
最小値は\(\small{ \ 2\cdot0+3\cdot0=0 \ }\)\(\small{ \ (x, \ y)=(0, \ 0) \ }\)のときになる。

ちなみに制約条件が同じで、\(\small{ \ 2x+y \ }\)の最大値と最小値を求める問題だったら、\(\small{ \ 2x+y=k \ }\)とおき、\(\small{ \ y=-2x+k \ }\)に変形すると今度は傾き\(\small{ \ -2 \ }\)になる。
傾き\(\small{ \ -2 \ }\)の直線を下から上へずらしていくと領域内を直線が通過し始めるのは原点を通るときで、通過し終わるのは\(\small{ \ x+y=3 \ }\)\(\small{ \ x \ }\)軸の交点を通るときってことがわかる。
このように指定された式を直線の形式に変形したときに傾きによって最大最小をとる点が変わってくるから、必ず図示して傾きを考えて最大最小をとる点を考えよう。
領域から最大最小の場所を決定
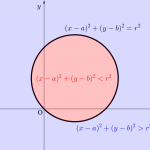
制約条件が不等式で領域を図示したら、領域のどの点で最大最小になるのか考えよう。最大最小になる点がわかったら、その点の座標を求めよう。領域が多角形なら二直線の交点、円なら接点が最大最小を満たす点になる。
次の与えられた条件のもとで、\(\small{ \ P \ }\)の最大値と最小値を求めよ。
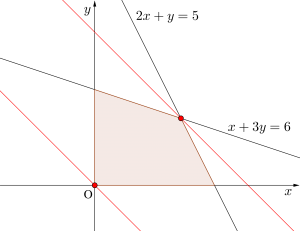
(1)\(\small{ \ x \geqq 0 \ }\)、\(\small{ \ y \leqq 0 \ }\)、\(\small{ \ 2x+y \leqq 5 \ }\)、\(\small{ \ x+3y \leqq 6 \ }\)のとき、\(\small{ \ P=x+y \ }\)
(2)\(\small{ \ x^2+y^2 \leqq 4 \ }\)、\(\small{ \ y \geqq -2x+5 \ }\)のとき、\(\small{ \ P=x+y \ }\)
(1)図より最大になるのは\(\small{ \ 2x+y =5 \ }\)、\(\small{ \ x+3y =6 \ }\)の交点を通るとき
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
2x+y =5\\
x+3y =6
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ x=\displaystyle \frac{9}{5}, \ y=\displaystyle \frac{7}{5} \ }\)
よって最大値は\(\small{ \ \displaystyle \frac{16}{5} \ }\)\(\small{ \ x=\displaystyle \frac{9}{5}, \ y=\displaystyle \frac{7}{5} \ }\)のとき
最小になるのは\(\small{ \ x=0, \ y=0 \ }\)のとき
よって最小値は\(\small{ \ 0 \ }\)\(\small{ \ x=0, \ y=0 \ }\)のとき
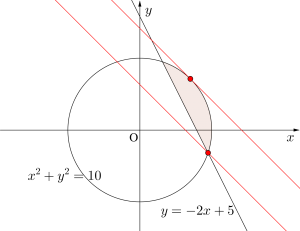
(2)\(\small{ \ x^2+y^2=10 \ }\)と\(\small{ \ y=-2x+5 \ }\)を連立して解くと
\(\small{ \ (x, \ y)=(1, \ 3)、(3, \ -1) \ }\)
不等式を満たす領域は図の色の部分になるから最小になるのは\(\small{ \ (x, \ y)=(3, \ -1) \ }\)を通るとき
よって最小値は\(\small{ \ 2 \ }\)\(\small{ \ x=3, \ y=-1 \ }\)のとき
最大になるのは\(\small{ \ x+y=k \ }\)とするとこの直線が\(\small{ \ x^2+y^2=10 \ }\)に接するとき
この2式を連立して
\(\small{ \ 2x^2-2kx+k^2-10=0\cdots① \ }\)
この方程式の判別式\(\small{ \ D =0\ }\)のとき接するので
\(\small{ \ \displaystyle \frac{D}{4}=k^2-2(k^2-10)=0 \ }\)
\(\small{ \ \therefore k=\pm2\sqrt{5} \ }\)
図より\(\small{ \ k=2\sqrt{5} \ }\)
\(\small{ \ k=2\sqrt{5} \ }\)を\(\small{ ①}\)に代入して\(\small{ \ x=\sqrt{5} , \ y=\sqrt{5} \ }\)
よって最大値は\(\small{ \ k=2\sqrt{5} \ }\)\(\small{ \ x=\sqrt{5} , \ y=\sqrt{5} \ }\)のとき

Point 不等式と領域と最大最小(1)
①制約条件の領域を図示しよう
②図示した領域から最大最小の点を決めよう
③点の座標を求めよう
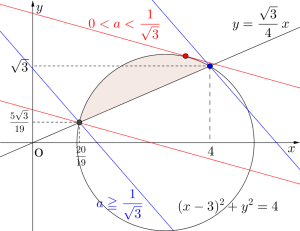
座標平面上の点\(\small{ \ (x, \ y) \ }\)に対し、\(\small{ \ f(x, \ y) \ }\)、\(\small{ \ g(x, \ y) \ }\)を次で定める。
\(\small{ \ f(x, \ y)=(x-3)^2+y^2-4 \ }\)、\(\small{ \ g(x, \ y)=\sqrt{3}x-4y \ }\)
(1)連立不等式\(\small{ \ f(x, \ y)\leqq0 \ }\)、\(\small{ \ g(x, \ y) \leqq 0 \ }\)の表す領域を\(\small{ \ D \ }\)とする。\(\small{ \ D \ }\)を図示せよ。
(2)円\(\small{ \ f(x, \ y)=0 \ }\)と直線\(\small{ \ g(x, \ y)=0 \ }\)の交点において、円\(\small{ \ f(x, \ y)=0 \ }\)と接する直線の方程式を求めよ。
(3)\(\small{ \ D \ }\)を(1)で定めた領域とする。点\(\small{ \ (x, \ y) \ }\)が領域\(\small{ \ D \ }\)内を動く時、\(\small{ \ ax+y \ }\)の最大値、最小値を求めよ。ただし、\(\small{ \ a \ }\)は正の定数である。
(1)\(\small{ \ f(x, \ y)=0 \ }\)と\(\small{ \ g(x, \ y)=0 \ }\)を連立して
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
(x-3)^2+y^2-4=0\cdots①\\
y=\displaystyle \frac{\sqrt{3}}{4}x\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ ②}\)を\(\small{ ①}\)に代入して
\(\small{ \ (x-3)^2+\displaystyle \frac{3}{16}x^2-4=0 \ }\)
\(\small{ \ 19x^2-96x+80=0 \ }\)
\(\small{ \ (19x-20)(x-4)=0 \ }\)
\(\small{ \ \therefore x=\displaystyle \frac{20}{19}, \ 4 \ }\)
よって円と直線の交点は\(\small{ \ \left(\displaystyle \frac{20}{19}, \ \displaystyle \frac{5\sqrt{3}}{19}\right) \ }\)、\(\small{ \ \left(4, \ \sqrt{3}\right) \ }\)となり、
領域\(\small{ \ D \ }\)は図の斜線部分になる。ただし境界線上も含む。

(2)(1)で求めた交点の座標より、\(\small{ \ f(x, \ y)=0 \ }\)に接する直線の方程式は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\left(\displaystyle \frac{20}{19}-3\right)(x-3)+\displaystyle \frac{5\sqrt{3}}{19}y-4=0\\
(4-3)(x-3)+\sqrt{3}y-4=0
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
37x-5\sqrt{3}y-35=0\\
x+\sqrt{3}y-7=0
\end{array}
\right.
\end{eqnarray} \ }\)
(3)\(\small{ \ ax+y=k \ (a \gt 0) \ }\)とおくと
\(\small{ \ y=-ax+k\cdots③ \ }\)
直線\(\small{③}\)と領域\(\small{ \ D \ }\)が共有点をもつときの\(\small{ \ k \ }\)の最大値と最小値を考えればよい。
(i)\(\small{ \ a \geqq \displaystyle \frac{1}{\sqrt{3}} \ }\)のとき
\(\small{③}\)が\(\small{ \ (4, \ \sqrt{3}) \ }\)を通るとき最大、\(\small{ \ \left(\displaystyle \frac{20}{19}, \ \displaystyle \frac{5\sqrt{3}}{19}\right) \ }\)を通るとき最小である。
(ii)\(\small{ \ 0 \lt a \lt \displaystyle \frac{1}{\sqrt{3}} \ }\)のとき
直線\(\small{③}\)が領域\(\small{ \ D \ }\)と接するとき最大、\(\small{ \ \left(\displaystyle \frac{20}{19}, \ \displaystyle \frac{5\sqrt{3}}{19}\right) \ }\)を通るとき最小である。
最大のとき、直線と円が接するから円の中心と直線の距離が円の半径に等しい
\(\small{ \ \displaystyle \frac{|a\cdot3+0-k|}{\sqrt{a^2+1}}=2 \ }\)より\(\small{ \ k=3a\pm2\sqrt{a^2+1} \ }\)
題意より\(\small{ \ k=3a+2\sqrt{a^2+1} \ }\)
最小のときは(i)と同様である。
最大値\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
4a+\sqrt{3}\left( \ a \geqq \displaystyle \frac{1}{\sqrt{3}} \ \right)\\
3a+2\sqrt{a^2+1}\left(0 \lt a \lt \displaystyle \frac{1}{\sqrt{3}}\right)
\end{array}
\right.
\end{eqnarray} \ }\)
最小値\(\small{ \ \displaystyle \frac{5(4a+\sqrt{3})}{19} \ }\)