こんにちは、リンス(@Lins016)です。
今回は領域を利用する一次式以外の最大最小について学習していこう。
領域は制約条件から図示しよう
前回の領域を利用する一次式の最大最小と同じで、まずは制約条件から領域を図示しよう。
ただ、前回と異なるのは、求める最大最小の式が二次式や分数式になっているんだ。
前回は最大最小の式が一次式だったから直線の式に変形して\(\small{ \ y \ }\)切片が求める値やそれに関係する値になったけど、今回はそうならない。
最大最小をとる式が何を示しているのかってことが重要になる。
\(\small{ \ P \ }\)の形で最大最小の点を判断
①\(\small{ \ P=x^2+y^2 \ }\)の場合
\(\small{ \ P \ }\)は原点からの距離の2乗を示すから、原点からの距離が最も遠い点と最も近い点を求める。
②\(\small{ \ P=(x-a)^2+(y-b)^2 \ }\)の場合
\(\small{ \ P \ }\)は点\(\small{ \ (a, \ b) \ }\)からの距離の2乗を示すから、点\(\small{ \ (a, \ b) \ }\)からの距離が最も遠い点と最も近い点を求める。
③\(\small{ \ P=\displaystyle \frac{y-b}{x-a} \ }\)の場合
\(\small{ \ P \ }\)は点\(\small{ \ (a, \ b) \ }\)から領域内の点に引いた直線の傾きを示すから、直線の傾きが最大になる点と最小になる点を求める。
与えられた式が最大最小になる領域内の点は、与えられた式からどの点になるか判断しよう。そして点を図に記入して、その点の座標を求めよう。
制約条件の不等式と領域
定期試験なら領域の最大最小だって気づくことは多いけど、いざ入試で領域の最大最小を利用しようって気づくのはなかなか難しい。
制約条件が図示できるような不等式だったら、領域を用いた最大最小になる可能性が高いから、制約条件つまり不等式をただの式と思わず領域にできないかって常に思っておくことが大事だからね。
次の与えられた条件のもとで、\(\small{ \ P \ }\)の最大値と最小値を求めよ。
(1)\(\small{ \ x\geqq0 \ }\)、\(\small{ \ y\geqq0 \ }\)、\(\small{ \ 1 \leqq x+2y \leqq 2 \ }\)のとき\(\small{ \ P=x^2+y^2 \ }\)
(2)\(\small{ \ (x-2)^2+(y-1)^2=5 \ }\)のとき\(\small{ \ P=\displaystyle \frac{y+2}{x+1} \ }\)
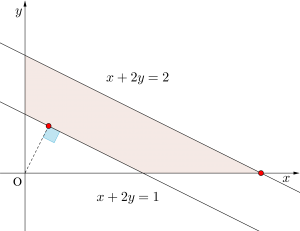
(1)\(\small{ \ x\geqq0 \ }\)、\(\small{ \ y\geqq0 \ }\)、\(\small{ \ 1 \leqq x+2y \leqq 2 \ }\)を図示すると図の色付きの部分になる
最大になるのは
\(\small{ \ (x, \ y)=(2, \ 0) \ }\)のとき最大値\(\small{ \ 4 \ }\)
最小になるのは\(\small{ \ x+2y=1 \ }\)とそれに垂直な原点を通る直線\(\small{ \ y=2x \ }\)との交点
\(\small{ \ (x, \ y)=\left(\displaystyle \frac{1}{5} , \ \displaystyle \frac{2}{5}\right)\ }\)のとき最小値\(\small{ \ \displaystyle \frac{1}{5} \ }\)
(2)\(\small{ \ y+2=P(x+1) \ }\)とすると、これは\(\small{ \ (-2, \ -1) \ }\)を通る傾き\(\small{ \ P \ }\)の直線になるから、この直線と円\(\small{ \ (x-2)^2+(y-1)^2=5 \ }\)が接するとき最大最小になるので
円の中心と直線の距離が半径と等しいとすると
\(\small{ \ \displaystyle \frac{|P\cdot 2-1+P-2|}{\sqrt{P^2+1}}=\sqrt{5} \ }\)
\(\small{ \ |3P-3|=\sqrt{5(m^2+1)} \ }\)
\(\small{ \ 2P^2-9P+2=0 \ }\)
\(\small{ \ \therefore P=\displaystyle \frac{9\pm\sqrt{65}}{4} \ }\)
よって最大値は\(\small{ \ P=\displaystyle \frac{9+\sqrt{65}}{4} \ }\)
最小値は\(\small{ \ P=\displaystyle \frac{9-\sqrt{65}}{4} \ }\)


Point 不等式と領域と最大最小(2)
①制約条件の領域を図示しよう
②どの点が最大最小になるのか考えて、その点の座標を求めよう
\(\small{ \ x\geqq0 \ }\)、\(\small{ \ y\geqq0 \ }\)、\(\small{ \ x+y\leqq 2 \ }\)のとき\(\small{ \ P=(x-2y+1)^2+(2x+y+2)^2 \ }\)の最大値を求めよ。
\(\small{ \ X=x-2y+1 \ }\)、\(\small{ \ Y=2x+y+2 \ }\)とおくと
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
X=x-2y+1\\
Y=2x+y+2
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて
\(\small{ \ x=-\displaystyle \frac{1}{5}X+\displaystyle \frac{2}{5}Y-1 \ }\)
\(\small{ \ y=\displaystyle \frac{Y-2X}{5} \ }\)
これを\(\small{ \ x\geqq0 \ }\)、\(\small{ \ y\geqq0 \ }\)、\(\small{ \ x+y\leqq 2 \ }\)に代入すると
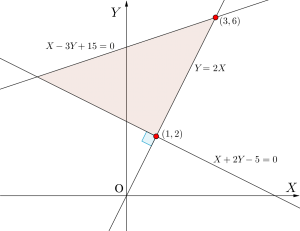
\(\small{ \ X+2Y-5\geqq0 \ }\)、\(\small{ \ Y-2X\geqq0 \ }\)、\(\small{ \ -X+3Y-15\leqq0 \ }\)となり、
\(\small{ \ XY \ }\)平面上に図示すると、次のようになる。
\(\small{\begin{eqnarray} \ P&=&(x-2y+1)^2+(2x+y+2)^2\\
&=&X^2+Y^2 \ \end{eqnarray}}\)
となるから原点から一番遠い点と近い点で最大値と最小値をとる
よって最大になるのは
\(\small{ \ Y=2X \ }\)と\(\small{ \ X-3Y+15=0 \ }\)の交点
\(\small{ \ (X, \ Y)=(3, \ 6) \ }\)のとき
最小になるのは
\(\small{ \ Y=2X \ }\)と\(\small{ \ X+2Y-5=0 \ }\)の交点
\(\small{ \ (X, \ Y)=(1, \ 2) \ }\)のとき
最大値\(\small{ \ 45 \ }\) \(\small{ \ (X, \ Y)=(3, \ 6) \ }\)のとき
最小値\(\small{ \ \ 5 \ }\) \(\small{ \ (X, \ Y)=(1, \ 2) \ }\)のとき