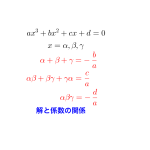こんにちは、リンス(@Lins016)です。
今回は1の3乗根とωについて学習していこう。
1の3乗根
\(\small{ \ 1 \ }\)の三乗根って\(\small{ \ x^3=1 \ }\)の解のことだよね。
実はこの\(\small{ \ 1 \ }\)の三乗根を利用する問題って結構あるからそれについて話をしていこう。
\(\small{ \ x^3=1 \ }\)
\(\small{ \ x^3-1=0 \ }\)
\(\small{ \ (x-1)(x^2+x+1)=0 \ }\)
\(\small{ \ x=1, \ \displaystyle\frac{-1\pm \sqrt{3}i}{2} \ }\)
\(\small{ \ x=1, \ \omega, \ \omega^2 \ }\)
1の三乗根
\(\small{ \ 1 \ }\)の三乗根(立方根)って、三乗して\(\small{ \ 1 \ }\)になる数だから\(\small{ \ x^3=1 \ }\)の解になる。だから、この方程式を解けばいいよね。
\(\small{ \ x^3-1=0 \ }\)
\(\small{ \ (x-1)(x^2+x+1)=0 \ }\)
\(\small{ \ x-1=0, \ x^2+x+1=0 \ }\)
\(\small{ \ \therefore x=1, \ \displaystyle\frac{-1\pm \sqrt{3}i}{2} \ }\)
つまり\(\small{ \ 1 \ }\)と\(\small{ \ \displaystyle\frac{-1\pm \sqrt{3}i}{2} \ }\)は\(\small{ \ 3 \ }\)乗すれば\(\small{ \ 1 \ }\)になる\(\small{ \ 1 \ }\)の三乗根ってことなんだ。
まずは1の三乗根の、この求め方を覚えておこう。
\(\small{ \ \omega \ }\)と\(\small{ \ \omega^2 \ }\)
\(\small{ \ 1 \ }\)の三乗根を求めるときに出てきた「\(\small{ \ x^2+x+1=0 \ }\)」っていう二次方程式だけど、実はこれってすごく有名な二次方程式なんだ。
高校数学で出てくる二次方程式で一番有名な二次方程式って言ってもいい。なんで、有名かと言うと、それはこの方程式の解に由来するんだ。
この\(\small{ \ x^2+x+1=0 \ }\)の解は\(\small{ \ x=\displaystyle\frac{-1\pm \sqrt{3}i}{2} \ }\)だったよね。
これをそれぞれ二乗してみよう。
\(\small{\begin{eqnarray} \ \left(\displaystyle\frac{-1+ \sqrt{3}i}{2}\right)^2&=&\displaystyle\frac{1-2\sqrt{3}i-3}{4}\\[3pt]
&=&\displaystyle\frac{-1- \sqrt{3}i}{2} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \left(\displaystyle\frac{-1-\sqrt{3}i}{2}\right)^2&=&\displaystyle\frac{1+2\sqrt{3}i-3}{4}\\[3pt]
&=&\displaystyle\frac{-1+\sqrt{3}i}{2} \ \end{eqnarray}}\)
これって\(\small{ \ x^2+x+1=0 \ }\)の解の一つを二乗すると、もう一つの解になってるよね。
つまり\(\small{ \ x^2+x+1=0 \ }\)の解の一つを\(\small{ \ \omega \ }\)とするともう一つの解は\(\small{ \ \omega^2 \ }\)って表すことができるんだ。
\(\small{ \ \omega \ }\)は\(\small{ \ x^2+x+1=0 \ }\)の解だから\(\small{ \ \omega=\displaystyle\frac{-1+ \sqrt{3}i}{2} \ }\)かもしれないし、\(\small{ \ \omega=\displaystyle\frac{-1- \sqrt{3}i}{2} \ }\)かもしれない。
でもどちらが\(\small{ \ \omega \ }\)でももう一つの解は\(\small{ \ \omega^2 \ }\)になるよね。
さらに\(\small{ \ x^2+x+1=0 \ }\)の解は\(\small{ \ 1 \ }\)の三乗根になるから、\(\small{ \ \omega^3=1 \ }\)が言える。
一般的に「\(\small{ \ 1 \ }\)の三乗根のうち、虚数であるものを\(\small{ \ \omega \ }\)とする」って言われてるんだ。
このことから\(\small{ \ 1 \ }\)の三乗根は\(\small{ \ 1, \ \omega, \ \omega^2 \ }\)になるからね。
ちなみに\(\small{ \ \omega \ }\)の満たす式は\(\small{ \ \omega^3=1 \ }\)と\(\small{ \ \omega^2+\omega+1=0 \ }\)が言えるから覚えておこう。

-

共役複素数と共役複素数の応用
共役複素数の基本から和と差と積と商の共役などについて詳しく解説しています。
続きを見る
\(\small{ \ \omega \ }\)の利用
\(\small{ \ \omega \ }\)を利用する問題に\(\small{ \ x^a+x^b+x^c \ }\)の因数分解がある。
f(ω)=0と因数分解
\(\small{ \ f(\omega)=0, \ f(\omega^2)=0 \ }\)が言えるなら、\(\small{ \ \left(x-\omega\right)\left(x-\omega^2\right) \ }\)、つまり\(\small{ \ x^2+x+1 \ }\) を因数にもつ。
\(\small{ \ x^7+x^5+1\ }\)の因数分解について考えてみよう。
\(\small{ \ f(x)=x^7+x^5+1 \ }\)とすると
\(\small{\begin{eqnarray} \ f(\omega)&=&\omega^7+\omega^5+1\\[3pt]
&=&\omega\left(\omega^3\right)^2+\omega^3\omega^2+1\\[3pt]
&=&\omega^2+\omega+1\\[3pt]
&=&0 \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ f(\omega^2)&=&\left(\omega^2\right)^7+\left(\omega^2\right)^5+1\\[3pt]
&=&\omega^2\left(\omega^3\right)^4+\left(\omega^3\right)^3\omega+1\\[3pt]
&=&\omega^2+\omega+1\\[3pt]
&=&0 \ \end{eqnarray}}\)
このことから\(\small{ \ x^7+x^5+1 \ }\)は\(\small{ \ x^2+x+1 \ }\)を因数に持つことがわかる。整式の割り算を利用すれば、\(\small{ \ (x^2+x+1)(x^5-x^4+x^3-x+1) \ }\)になることがわかる。
\(\small{ \ x^a+x^b+x^c \ }\)の因数分解を考えるとき、\(\small{ \ f(\omega), \ f(\omega^2) \ }\)の値が\(\small{ \ 0 \ }\)にならないか調べてみよう。
これをふまえて過去に出題された入試問題にチャレンジしてみよう。
多項式\(\small{ \ (x^{100}+1)^{100}+(x^2+1)^{100}+1 \ }\)は多項式\(\small{ \ x^2+x+1 \ }\)で割り切れるか。
\(\small{ \ f(x)=(x^{100}+1)^{100}+(x^2+1)^{100}+1 \ }\)とする
\(\small{ \ x^2+x+1=0 \ }\)を解くと\(\small{ \ x=\displaystyle\frac{-1\pm\sqrt{3}i}{2} \ }\)
\(\small{ \ \omega=\displaystyle\frac{-1+\sqrt{3}i}{2} \ }\)とすると、\(\small{ \ \omega^2=\displaystyle\frac{-1-\sqrt{3}i}{2} \ }\)
また\(\small{ \ (x-1)(x^2+x+1)=0 \ }\)より\(\small{ \ \omega^3=1 \ }\)になる
さらに
\(\small{ \ f(\omega)=0, \ f(\omega^2)=0 \ }\)より\(\small{ \ (x^{100}+1)^{100}+(x^2+1)^{100}+1 \ }\)は\(\small{ \ x^2+x+1 \ }\)で割り切れる
解と係数の関係と\(\small{ \ \omega \ }\)
解と係数の関係ってあるよね。
-

解と係数の関係
解と係数の関係を利用した問題や解と係数の関係の利用について詳しく解説しています。
続きを見る
この解と係数の関係を利用する問題で、次のような問題に気をつけよう。
\(\small{ \ x^2+x+1=0 \ }\)の解を\(\small{ \ \alpha, \ \beta \ }\)とするとき、次の値を求めよ。
(1)\(\small{ \ \alpha^7+\beta^7 \ }\)
(2)\(\small{ \ \alpha^5+\alpha^3+\alpha \ }\)
解と係数の関係より
\(\small{ \ \alpha +\beta=-1, \ \alpha\beta=1 \ }\)
また\(\small{ \ x^2+x+1=0 \ }\)より
\(\small{ \ (x-1)(x^2+x+1)=0 \ }\)
\(\small{ \ x^3-1=0 \ }\)
\(\small{ \ \therefore \alpha^3=\beta^3=1\ }\)
(1)
\(\small{\begin{eqnarray} \ \alpha^7+\beta^7&=&\alpha(\alpha^3)^2+\beta(\beta^3)^2\\[3pt]
&=&\alpha+\beta\\[3pt]
&=&-1 \ \end{eqnarray}}\)
(2)
\(\small{\begin{eqnarray} \ \alpha^5+\alpha^3+\alpha&=&\alpha^2\alpha^3+\alpha^3+\alpha^2\\[3pt]
&=&\alpha^2+\alpha+1\\[3pt]
&=&0 \ \end{eqnarray}}\)
この問題を見てわかるけど、与えられた式の解が\(\small{ \ 1 \ }\)の三乗根になることに気付かないと解くの大変だよね。
だから\(\small{ \ x^2+x+1=0 \ }\)を見たら解が\(\small{ \ \omega, \ \omega^2 \ }\)だって気付かないといけないよね。
仮に気付かなくても、問題の\(\small{ \ \alpha^7+\beta^7 \ }\)の\(\small{ \ 7 \ }\)乗ってところもポイントになってるよね。三乗や四乗、五乗ぐらいなら対称式って感じするけど、それ以上だと計算できなくはないけど、大変だもんね。
Point \(\small{ \ 1 \ }\)の三乗根と\(\small{ \ \omega \ }\)
①\(\small{ \ 1 \ }\)の三乗根は\(\small{ \ 1, \omega, \ \omega^2 \ }\)
②\(\small{ \ x^2+x+1=0 \ }\)の解は\(\small{ \ x=\omega, \ \omega^2 \ }\)
③\(\small{ \ x^a+x^b+x^c \ }\)の因数分解に\(\small{ \ \omega \ }\)を利用する