こんにちは、リンス(@Lins016)です。
今回は三角比の方程式と不等式(基本)について学習していこう。
単位円を利用した三角比の方程式と不等式の解き方
三角比の方程式や不等式から角度を求める問題の場合は単位円を利用して問題を解いていくようにしよう。問題演習をたくさんこなして、単位円を扱うことに慣れておこう。そうすればさっと問題が解けるようになるからね。
\(\small{ \ \sin\theta \ }\)
単位円上の動点の\(\small{ \ y \ }\)座標
\(\small{ \ \cos\theta \ }\)
単位円上の動点の\(\small{ \ x \ }\)座標
\(\small{ \ \tan\theta \ }\)
原点と動点を結ぶ直線と\(\small{ \ x=1 \ }\)の交点の\(\small{ \ y \ }\)座標
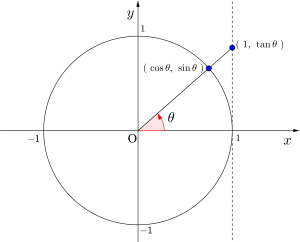
今回学習する解き方は図形と計量(数学I)と三角関数(数学Ⅱ)で出題される方程式・不等式の基本的な解き方になるから、きちんと理解して完璧に解けるようにしておく必要があるから必ず押さえておこう。
\(\small{ \ \sin \theta \ }\)(正弦)の方程式と不等式
\(\small{ \ \sin \theta= a \ }\)といった正弦の値から角度を求める三角比の方程式は、単位円と直線\(\small{ \ y=a \ }\)の交点と原点を結ぶ動径の\(\small{ \ x \ }\)軸からの回転角がその答えになる。
基本的に角度を求める問題に、三角比の表を用いて解くような問題はほとんどない出題されない。
つまり求める角度は有名角になるから有名角の三角比の値をきちんと覚えておこう。
次に\(\small{ \ \sin \theta \geqq a \ }\)などの正弦の値から角度の範囲を求める三角比の不等式は、単位円と直線\(\small{ \ y=a \ }\)の交点と原点を結ぶ動径の\(\small{ \ x \ }\)軸からの回転角\(\small{ \ \theta \ }\)が、与えられた不等式を満たす範囲の値がその答えになる。
この不等式を満たす範囲を単位円上に書いて答えを導こう。
\(\small{ \ 0^{\circ} \leqq \theta \leqq 180^{\circ} \ }\)のとき次の方程式、不等式を解け。
(1)\(\small{ \ \sin \theta = \displaystyle \frac{1}{2} \ }\)
(2)\(\small{ \ \sin \theta \geqq \displaystyle \frac{\sqrt{3}}{2}\ }\)
(1)図より\(\small{ \ \theta=30^{\circ}, \ 150^{\circ} \ }\)
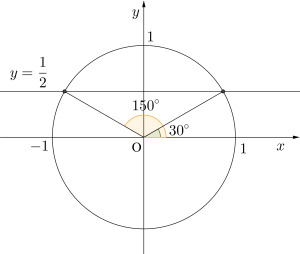
(2)図より求める範囲は\(\small{ \ 60^{\circ} \leqq \theta \leqq 120^{\circ} \ }\)
\(\small{ \ \cos \theta \ }\)(余弦)の方程式と不等式
\(\small{ \ \cos \theta= a \ }\)といった余弦の値から角度を求める三角比の方程式は、単位円と直線\(\small{ \ x=a \ }\)の交点と原点を結ぶ動径の\(\small{ \ x \ }\)軸からの回転角がその答えになる。
\(\small{ \ \cos \theta \geqq a \ }\)などの余弦の値から角度を求める三角比の不等式は、単位円と直線\(\small{ \ x=a \ }\)の交点と原点を結ぶ動径の\(\small{ \ x \ }\)軸からの回転角\(\small{ \ \theta \ }\)が、与えられた不等式を満たす範囲の値がその答えになる。
だからこの不等式を満たす範囲を単位円上に書いて答えを導こう。
\(\small{ \ 0^{\circ} \leqq \theta \leqq 180^{\circ} \ }\)のとき次の方程式、不等式を解け。
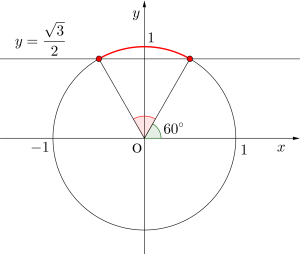
(1)\(\small{ \ \cos \theta = \displaystyle \frac{1}{2} \ }\)
(2)\(\small{ \ \cos \theta \leqq \displaystyle \frac{\sqrt{3}}{2}\ }\)
(1)図より\(\small{ \ \theta=60^{\circ} \ }\)
(2)図より求める範囲は\(\small{ \ 30^{\circ} \leqq \theta \leqq 180^{\circ} \ }\)

\(\small{ \ \tan \theta \ }\)(正接)の方程式と不等式
\(\small{ \ \tan \theta= a \ }\)といった正接の値から角度を求める三角比の方程式は、直線\(\small{ \ x=1 \ }\)上に点\(\small{ \ (x, \ a) \ }\)をとり、この点と原点を結ぶ直線と単位円との交点と原点をむすぶ動径の\(\small{ \ x \ }\)軸からの回転角がその答えになる。
\(\small{ \ \tan \theta \geqq a \ }\)などの正接の値から角度を求める三角比の不等式をは、直線\(\small{ \ x=1 \ }\)上の点\(\small{ \ (x, \ a) \ }\)と原点を結ぶ直線と単位円との交点と原点を結ぶ動径の\(\small{ \ x \ }\)軸からの回転角\(\small{ \ \theta \ }\)が、与えられた不等式を満たす範囲がその答えになる。
だから、この不等式を満たす範囲を単位円上に書いて答えを導こう。
ただし、\(\small{ \ \tan 90^{\circ} \ }\)は存在しないから注意しよう。
\(\small{ \ 0^{\circ} \leqq \theta \leqq 180^{\circ} \ }\)のとき次の方程式、不等式を解け。
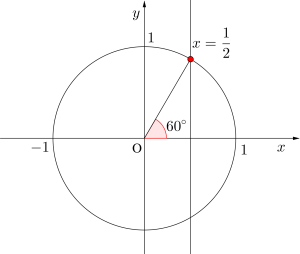
(1)\(\small{ \ \tan \theta = \displaystyle \frac{1}{\sqrt{3}} \ }\)
(2)\(\small{ \ \tan \theta \leqq -\sqrt{3}\ }\)
(1)図より\(\small{ \ \theta=30^{\circ} \ }\)

(2)図より求める範囲は\(\small{ \ 90^{\circ} \lt \theta \leqq 120^{\circ} \ }\)


Point 三角比の方程式と不等式(基本)
①有名角の値を覚える
②不等式の範囲を単位円上に書こう

